流れ 2001年10月号 目次
― 生物と流れ ―
海外研究動向
学生の欄
| リンク一覧にもどる | |
CFDで見る生物流れ
|
▲劉 浩 |
魚や昆虫及び鳥ほど流体力学の原理を巧みに利用し水中や空中を遊泳する人工物はない.これらの生物運動の陰には,今後の流体力学発展のキーが無数に隠されているといっても過言ではない.生物飛翔を例にあげよう.地球上,およそ百万種類の昆虫と約10,
000種の鳥やバットは,大空を自由自在に舞う.過去100年の間,航空技術は飛躍的に発展してきたが,しかし15億年以上もの進化を成し遂げてきた自然界の飛行体は,人間にとってはいつまでも魅力的である.人間は,最高速度約4~5身長/秒で移動できるという.地上をもっとも速く走り抜ける動物と言われるチータのトップ速度は,約18体長/秒となる.人工飛行体の傑作,米国製の超音速戦闘機SR71
(別名Blackbird)は,最高速度がマッハ3(~2000マイル/時)ともなり,およそ32機長/秒に達する.一方,普通の鳩でも,通常50マイル/時の速度で悠々と大空を飛んでおり,これは何と秒速75体長にも匹敵する.飛行体のロール運動を見てみても,高度な曲技飛行(aerobatics)能力を有する.例えば米国製のA-4
Skyhawkのような飛行機のロール率は,毎秒約720度と言われるが,つばめはその9倍もの5000度以上のロール率をこなせる.最大許容の正の重力加速度は,普通航空機は4-5G,
軍用機は8-10Gであるに対して,多くの鳥は何と毎日100回以上に10-14Gの重力加速度を経験している.
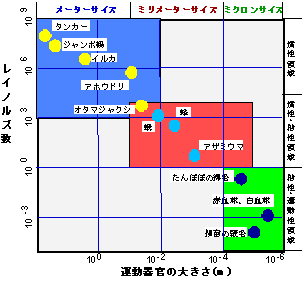
自然界の様々な生物流体現象を,それら運動器官の大きさ,と流体の慣性力と粘性力の比であるレイノルズ数の相関で整理してみると(図1)サイズによって流体現象・流体力の発生メカニズムが異なることが明らかになってくる.我々が馴染んでいる飛行機や船などの,いわゆるメーターサイズ領域に於ける流体現象は,レイノルズ数(Re>105)が高くて慣性力が支配的になっているものであって,流体力学理論も相当確立されている.例えば人間や渡り鳥が多くの恩恵を受けた流線型は,安定な流体力を発生できる優れた運動器官であることは言うまでもない.しかし,地球上の動物の大半を占める小さな生物(主に昆虫)が棲息するミリメーターサイズの領域では,レイノルズ数が
100<Re<104となり慣性力と粘性力が互角に働くようになっており,流体力の働き方はレイノルズ数の大きい領域とは相当に異なっている.このために例えば,よく見受けられる昆虫の羽は平板の様な形をしており激しく羽ばたくことによって流体力を発生する.
生物流体の現状
生物流体の先駆者的存在であるCambridge大学動物学科の教授であったGrayは,1930年代から1960年代前半にかけて,生物運動及び生物流体現象を力学的原理を用いて説明するために,魚の運動について精力的に基礎研究を展開し多くの計測結果を得られた.1960年代から1970年代半ばにかけて,イギリスのLighthillやアメリカのWuを始め,多くの生物学者や,応用数学者及び工学者が参入してきて,水棲動物のみならず鳥をはじめ多くの生物の推進法に対して,ポテンシャル理論を用いた生物流体力学理論の体系化を構築した.ところが,その後つい最近の1990年代後半までに,大きな前進があまり見られなかった.これは,決して我々が生物の運動に潜んでいる優れたメカニズムを全部分かったわけではなく,むしろ従来の生物流体力学理論が限界に来ているのではないかと思われる.その理由は,激しい運動をこなす生物まわりの流れが大きな渦構造が伴うダイナミックなものであって,生物流体力学の基礎になっている航空流体力学を基にした定常あるいは準定常の線形理論が通用しなくなってしまうことが最近になって漸く分かった.つまり,生物流体は,通常複雑な非線形現象であり,故により高度な計測技術や解析理論を開発しない限り更成る発展が望めない段階まできたと思われる.現在,生物学者(中にCambridge大学動物学科のC.
Ellington教授のグループとUC Berkeley校のM. Dickinson教授のグループが両大陣営になっている)を中心とした,生物モデル実験と,工学者を中心とした計算力学モデリングが2つ代表的な研究分野になりつつある.ここで,著者が近年計算流体力学(CFD:
computational fluid dynamics)的手法を用いた解析結果を紹介しながら生物の遊泳及び飛翔に関する流体現象を見てみる.
水中生物まわりの流れ
水中生物は,通常波打ち運動をしながらジェット状の後流を発生しその反力を推進力として泳いでいる.この推進メカニズムは,無次元周波数(ストローハル数)のごく狭い範囲内(魚の場合はおよそ0.2~0.3)において最適現象を示す.魚がどのようにジェット推進を発生しているのか,叉は各器官の相互干渉を利用できるのかといった問題を説明するため,魚のような流線型とかけ離れた球状の頭に細長い尻尾をもつオタマジャクシ(Tadpole)の運動メカニズムを2次元および3次元CFD解析の結果で見てみる.
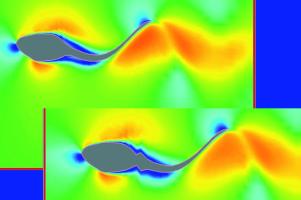
図2に2次元モデルまわりの足有と無し両場合の流れ様相を示す.尻尾根元近傍において剥がれた厚い境界層,すなわち「死水領域」(dead
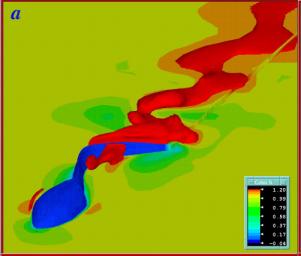
water zone)ができており,後流にvon Karman渦のような,逆方向に回転する渦列と加速されたジェット流が見られる.両場合もさほどの相違をみせていないことに注目されたい.生物学的観点からみると,これは大きな意味を持っており,つまりオタマジャクシの独特な形態が彼等の蛙への変態に適合していると思われる.一方,オタマジャクシの実形状による遊泳メカニズムへの3次元効果を確認するため,図3に3次元モデル周囲および後流の様相を示す.後流中心に見られる強いジェット流をもつ渦列の様相は,MITのRobotic-tunaまわりの可視化された結果と良好な一致を示す.後流の渦列に比べて,尻尾が激しい横振動しているにも拘わらず縦渦が殆ど見受けられない.これは,タマジャクシが自分の形態にあった波打ち運動をしている最適現象と,2次元モデルでも定性的に正しい結論を導くことができることを意味する.ただし,定量的には3次元モデルの推進力が2次元の場合に比べて振幅がかなり減衰され,1周期平均値がトリムの取れた(零)状態に近いことが分かった.
飛翔生物まわりの流れ
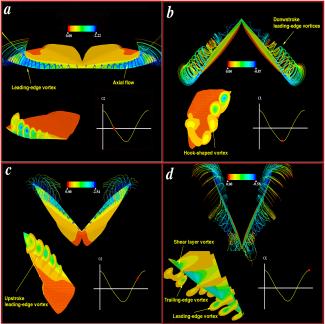
昆虫や鳥は,羽ばたき運動によって自分の体重を支える揚力と飛ぶための推進力を同時に発生する.そのため,常に打上げと打下しの並進運動(translation)と,打上げと打下ろしをつなぐための回転運動(rotation)とのような複雑な運動をこなす.昆虫羽ばたき運動の中に潜んでいる独特な流体現象を例にあげる.Cambridge大学のEllington教授のご協力で図4のような蛾(hawkmoth)の翼形状及運動に関するデータを提供してもらいシミュレーションを行った.ジャンボ機などに比べてはばたく羽まわりの流れの速度は音速に比べて非常に遅く,密度が一定である非圧縮性流体を仮定している.計算モデルは,従来の流体力学理論がもっとも苦手にしている前進速度無しの,いわゆる羽から生じる揚力と昆虫の体重と釣り合い空中に静止している場合を想定したホバリング飛翔である.
昆虫の羽ばたき運動が複雑のため,それに伴う羽周囲の流れは,流線型のような翼型まわりの滑らかな流れとは相当に異なり,dynamic的な渦流れとなる.従来の流体力学の準定常理論は,羽ばたき1周期の各時刻において同じ迎え角と流入速度を持つ定常流を解析することによって昆虫飛翔を説明してきた.しかし,最近になってこれらの理論によって計算された揚力では,昆虫が自分の体重を支えられなくて墜ちてしますことが分かってきた.つまり,昆虫の羽は,きっと何かのメカニズムを巧みに用いてより多い揚力を発生しているに違いない.そのメカニズムは,図4に示されるように,羽が打上げと打下ろし時,羽の前翅に現われる強い前縁渦(leading-edge
vortex)にあるということが最近の研究で分かってきた.羽の打下ろし全過程において,強い前縁渦が見られ,しかもこの渦を安定させる役割のある軸流れをもってスパイラルに回転しながら羽端に向かって行く様相がきれいに取られている.この前縁渦が打下ろし初期に生じて,水平位置に達した時最も発達しており,更に回転運動に伴って翼面上から剥がれていく.計算結果は,Cambridge大学で行われた蛾の翼模型による煙可視化実験の結果(図5)と良好な一致を示す.この前縁渦は,羽面上に大きな負圧領域をもたらし準定常理論計算値の2倍以上の揚力を発生させている.最近もう一つbreakthrough的な研究で,より小さい,例えばハエぐらいの昆虫は,前縁渦以外回転メカニズムをも利用しているというふうに報告されている.これは,つまり昆虫の世界の中でも,サイズまたは形態によって,飛行メカニズムにバリエーションがあることを意味する.
生物流体の今後展望
複雑な運動をする生物まわりの流体がどう振る舞うかを更に理解するには,より高度な実験および計算流体力学的手法の開発が期待される.その中で,従来の生物流体力学から新しい分野が派生してくる可能性が十分あると思われる.生物流体を一種の知能性を有する流体現象と取ら方もできる.例えば,生物運動の最適メカニズムに関する流体ー構造連成問題,表面構造および知的乱流制御に関するマイクロ流体問題,生物外部・内部流体の相互干渉による物質交換・輸送問題等が挙げられる.生物の運動メカニズムの解明は,マイクロマシンおよびミリマシンの設計に必要な新しい流体力学的理論の確立および新しい設計ツールの開発に大いに役に立つと考えられる.アメリカでは,2年程前からDARPAがスポンサーになったセンチミリサイズの人工飛行体,すなわちMAV(Micro
Air Vehicle)を研究・開発するプロジェクトが,産官学各機関にて次々立ち上げられてきており,生物流体の研究がいよいよ基礎研究から応用研究へとコマを進めはじめている.一方,高レイノルズ数流体現象(機構)に応用できる未知のメカニズムを見つかる可能性をも示すかもしれない.高速魚や鳥に学んで,航空や造船工学に応用できそうな乱流の知的制御による流体抵抗低減に関する研究も最近盛んに行われるようになった.これは,停滞しつつある乱流の研究に新しい風を吹き込むだけではなく省エネなどの多分野に大きな波及効果がある.
更新日:2001.10