流れ 2002年9月号 目次
― 特集 渦法 ―
｜ リンク一覧にもどる ｜ |
渦法に関する理論的な話題
大阪府立大学工学研究科 木田 輝彦
1．まえがき
渦法は1931年にRosenheadがKelvin-Helmholtz不安定性について計算したことに始まると言われている．その後，1973年にChorinが円柱まわりの渦法による数値解析を発表して以来，この手法に関する研究が急速に発展した．これらについては，1997年にYing and Zhang[1]，2000年にCottet and Koumoutsakos[2]によって成書の形で発表されている．前者は数理的研究を中心に，後者は著者等の研究グループによる一連の研究を踏まえて，数理的な基礎から乱流も視野に入れた数値アルゴリズムに至る広い範囲でまとめられている．
2．渦法の基礎
渦法は，Navier-Stokes方程式から導出される渦度輸送方程式を次の2段階のステップを用いて構成されている．
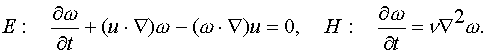（１）
特性曲線を導入すると，解法 Eは次のようになる．
（２）
速度場はBiot-Savartの式から求められる．
渦法をこれらのステップを用いて表現すると，次のようになる．
nは時間ステップである．これらは，1次と2次精度のスプリット法で，それらの精度はそれぞれ
であることが，Beale
and Majda[3]によって明らかにされている．これらの解析は，境界のない場合であり，境界があるとそこでは滑りなし等の速度場の境界条件が必要となる．渦度場を数値的に求める渦法では，この境界条件が陽的に与えられていないため，どのようにアルゴリズムに入れるかが問題となる．
Chorin and Marsden[4]は渦度生成のアルゴリズム：
を導入し，次のアルゴリズムを提案している．
（３）
τは境界の接線方向単位ベクトル，～はωを全空間に拡張した渦度場，δはデルタ関数である．
3．渦度生成
渦度生成アルゴリズムを示す式[3]は，速度場を奇関数的に領域外に拡張し，境界のない流れ場全体で拡散方程式を解くことに対応しているこの問題は，Benfatto
and Pulvirenti[6]が半無限空間に関して数理的に厳密に解析した．彼等は境界に対し接線方向速度成分は奇関数とし，法線方向は偶関数として境界外部に拡張して解析した．その精度は
である．Ying[7]は，凸領域に拡張しこれら両手法の収束性について証明している．木田ら[5]は境界外部への拡張の仕方に係わらず，境界面での滑り速度に対応する渦度を生成すればよいことを明らかにした．Cottet[8]は次の渦生成アルゴリズムを提案し，Navier-Stokes方程式の場でその収束性を証明している．
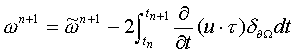
4．Vortex blob法とParticle strength exchange[PSE]法
渦法は式(2)に示すように粒子法の一つであり，Lagrange的に流れを求める．その際，連続して分布する渦度場を離散化し，有限の離散渦ωhで流れを近似する．このために，cut-off関数ζ(x)が導入される．
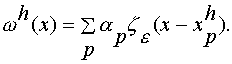
ただし，
で，dは流れの次元数である．
まわりの循環(circulation)と言われているが，正確には循環ではなく三次元流れではベクトル量で,
である．
は流体要素の微小体積である．このような離散化に対する整合性や収束性は明らかにされており，その際，cut-off半径εが離散距離hより大きく取ることが要請されているが，点渦に関するHou
et al.[9]の研究によって，滑らかな解が存在するならばこの条件は特に必要ではなく，精度は
である．
PSE法は拡散方程式Hの右辺を積分表示で近似するもので，Mas-Gallicによって1987年に導入されたのが始まりである[2]．
ただし，
であり，次の条件を満たす．
このPSE法の概念は，微分を積分表示で表されることを意味しているため，広い発展が期待される．例えば，粒子を含む2相流[10]，音場解析も考慮した渦法の圧縮性流れへの応用[11]や乱流流れへの発展[12]である．cut-off関数はfilteringの役目をしている点に注目し，Subgrid-scaleの乱流モデルがPSE法を用いて提案されている[13]．
Vortex blob法とPSE法とは基本的には同じ概念であるが，Vortex blob法では渦度場の精度が速度場より悪くなるので，計算精度を高めるために微分操作を無くしたのがPSE法と考えられる．
5．計算例
我々がこれまでに計算してきた一例を示す．図1に示す二次元矩形柱まわりの流れはVortex blob and sheet法（濃い点）とCottet提案の格子点に渦点を再配置するRemeshing法（薄い点）により計算した離散渦分布の比較である．一様流が矩形にあたった瞬間からの過渡的な流れを示している．図2に示す三次元流れの例は，ｚ軸方向に一様流が流れている場にxy面上に渦輪（渦点数ｎ）を時間ステップ毎に発生したとした場合の渦輪の干渉をVortex blob法とPSE法により計算した等渦度面である．PSE法では格子は用いず，渦の粘性拡散と伸縮にPSE法を用いている．
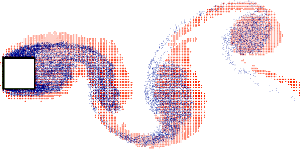
図1：Vortex
blob and sheet法（濃い点）とRemeshing法（薄い点）との比較（t=14.28）
 （a） Vortex blob法（n=20） |
 （b） PSE法（n=50） |
| 図2：Vortex blob法とPSE法との比較[t=3] | |
6．文献
[1] Ying, L-a. and Zhang, P., Vortex Methods,
Science Press/Kluwer Academic Publishers, Beijing, [1997].
[2] Cottet, G-H. and Koumoutsakos, P.D., Vortex Methods:
Theory and Practice, Cambridge Univ. Press, UK, [2000].
[3] Beale, J.T. and Majda, A., Math. Comp., 37 [1981], 243-259.
[4] Chorin, A, et al., Comm. Pure Appl. Math., 31 [1978],
205-256.
[5] 木田他2名, 機論, 63-615, B[1997], 3491-3498.
[6] Benfatto, G. and Pulvirenti, M., Comm. Math. Phys.,
96 [1984], 59-95, and Comm. Math. Phys., 106 [1986], 427-458.
[7] Ying, L-a., Vortex Methods, Selected Papers of the 1st
Inter. Con. on Vortex Methods. [ed. Kamemoto, K. and Tsutahara,
M.], World Scientific, Singapore, [2000], 115-122.
[8] Cottet, G.-H, Navier-Stokes equations and related nonlinear
problems, [ed. Sequeira, A.], Plenum Press, [1995].
[9] Hou, T.Y. and Lowengrub, J., Comm. Pure Appl. Math.,
43 [1990], 965-981.
[10] Walther, J.H. and Koumoutsakos, P., J. Com. Phys.,
167 [2001], 39-71.
[11] Eldredge, J. Colonius, T. and Leonard, A., AIAA 2001-2641.
[12] Cottet, G.-H, et al., J. Comp. Phys., 175 [2002], 701-712.
[13] Cottet, G.-H., Anisotropic subgrid-scale numerical
schemes for Large Eddy Simulations of turbulent flows,
http://www-lmc.imag.fr/lmc-edp/Georges-Henri.Cottet/