流れ 2004年12月号 目次
― 特集:ナノ・マイクロスケールの熱流動 ―
| リンク一覧にもどる | |
マイクロTASのためのマイクロ混合器
 東京大学 生産技術研究所 鈴木 宏明 |
1.概論
近年,反応容器や流路システムをチップ上に集積化・微小化し,生化学反応の分析・検査を統合化して行う研究分野が急速に発展しており,マイクロ TAS ( Micro Total Analysis Systems )または Lab-on-a-Chip と呼ばれている [1] .各種の DNA チップ,タンパク質検出や相互作用分析装置,また細胞培養チップなどが代表的な例である.これらの反応は,ほぼ例外なく溶液の状態で行われるため,この分野において熱流体工学が果たす役割は大きい.
マイクロ TAS において扱われる流路・容器の代表的スケールは 1~100µm であり,その代表レイノルズ数は 10-6 ~102 の範囲が一般的である.この領域では,流れは層流であり,多くの場合はく離も発生しないクリープ流れとなる.このように,微量かつ低レイノルズ数の液体の制御においては,送液方法,表面張力の影響,電気二重層の影響,気泡の除去など,マクロスケールとは違った様々な問題が浮かび上がってくる.その中で,混合(攪拌)も重要な課題である.
マクロスケールにおける混合促進手法は,乱流やはく離を利用するのが一般的である.しかし,低レイノルズ数領域では,混合は基本的に分子拡散のみに依存する.マイクロ流路中では,分子量の小さな物質は比較的すばやく拡散するが, DNA ,タンパク質,細胞など大きな分子量の物質は,拡散が終了するのに膨大な時間がかかってしまう.たとえば,染料やイオン(拡散係数 10-9 [m2/s] )が 100µm の距離を拡散するのに必要な時間は約 10秒であるが, 1µm の球形物質(拡散係数 10-13[m2/s] )の場合, 105 秒を要する.
クリープ流れの領域において混合を促進するための手法として,カオス混合という概念がある [2] .この場合のカオスは,流れをラグランジュ的に見たとき,初期の微小な差異が,時間とともに指数的に増大する系として定義される.要素の引き伸ばし・折りたたみのメカニズムが内在する系は,カオス的になる可能性がある.
当研究室では,磁気ビーズ [3] を用いた細胞の選別(ソーティング)システムのマイクロチップ化に関する研究を行っている.細胞膜の表面に存在する固有の膜タンパク質に特異的に吸着する抗体で磁気ビーズを表面修飾し,様々な細胞の混合溶液と混ぜると,磁石によって目的の細胞のみを非侵襲で取り出すことができる.このとき,磁気ビーズと標的細胞をよく攪拌し,接触確率を増加させることが,高効率化への鍵となる.本研究では,マイクロ流路内で磁気ビーズの運動をカオスに導き,効率よく撹拌するための混合器に関する研究を行った.
2.マイクロカオス混合器のデザイン
混合器は,MEMS技術を用いて,シリコン基板上にマイクロ電極群及びマイクロ流路を集積化して製作した.電極群に制御信号を与えて変動磁場を発生させ,流路中の磁気ビーズを撹拌する.図1に,デバイス及び磁場発生原理の模式図を示す.隣り合う電極のペアにそれぞれ対向する方向に電流を与えると,それらの中心に引き寄せられる向きに磁場が発生する.計算により,500mAの電流を与えた時,電極の中心付近で最大40ガウス程度の磁界が発生することを確認した.このとき,流路内液中に含まれる直径1µm,酸化鉄含有率12wt%の磁気ビーズに0.3pNの力が働き,30µm/sの終端速度が得られる.
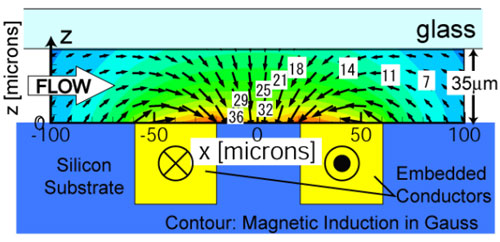
図1.磁気ビーズマイクロ混合器における磁場発生原理の模式図(断面).
マイクロ電極群によって溶液中の磁性粒子を操作可能であることが確かめられたが,カオス混合を実現するためには,さらに流路及び電極形状,また制御信号を工夫する必要がある.本研究では,図2に示される蛇行流路及び垂直配列電極を考案した.図は混合部の1ユニットを示し,x方向に繰り返される.ベクトルは流路中の定常速度場を,1~4の黄色の長方形は電極を示す.図3に,各電極に与える制御信号(位相シフト信号)を示す.例えば,位相(iv)では電極3及び4に対向電流が印加され,流路中の磁性粒子はコーナー部分の低速領域に引き寄せられる(図2中矢印①).一方,位相(iii)では,電極2と3に電流が印加され,低速領域に滞留している粒子は高速領域にもどされる(図2中矢印②).このように,電流を与える電極のペアを順次シフトしていくことにより,擬似的に引力・斥力を得る.
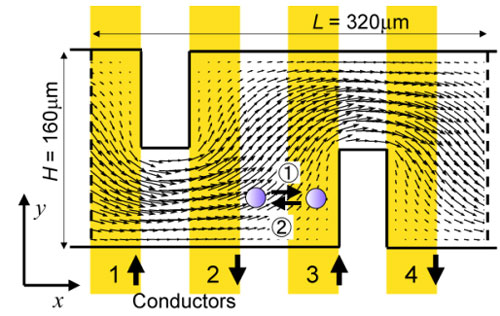
図2.カオス混合のための蛇行形状マイクロ流路.
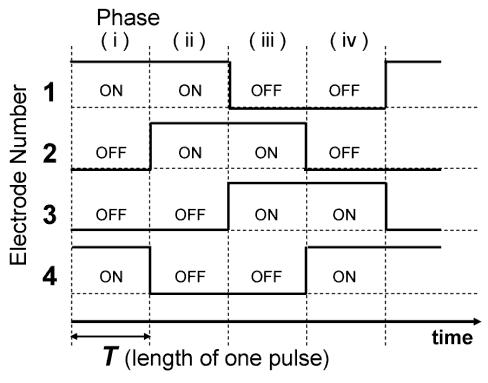
図3.各電極に与える制御信号(位相シフト信号).
本手法に最適な制御周波数および電磁力を決定するため,one-way coupling法により二次元での数値シミュレーションを行い,磁気ビーズの粒子軌跡を求めた.流路幅H,1ユニットの長さLはそれぞれ160µm,320µmとし,バルク平均流速Vは80µm/sに固定して解析を行った.図4にその結果の一例を示す.図中赤と青の長方形は初期条件を表す.磁力を与えない場合はビーズに働く力が流体の粘性抗力のみであり,粒子は流線に完全追従するため,赤と青のビーズは混じり合わない(図4a).一方,位相シフト信号を与えた場合(ストローハル数St=H/VT=8.3),ビーズ群の引き伸ばし・折りたたみが繰り返し発生し,赤と青の粒子群は層状に重なり,カオス的なパターンを形成する(図4b).
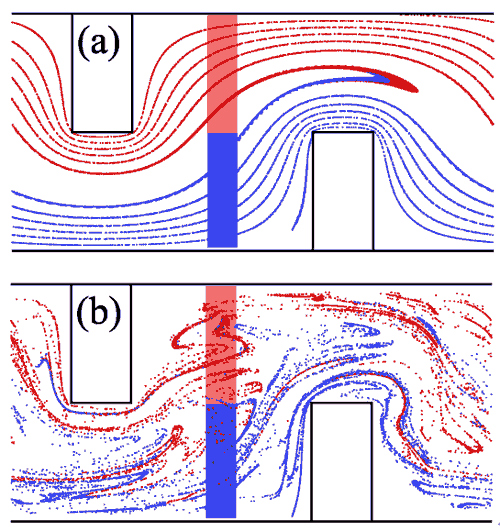
図4.蛇行流路内の磁気ビーズの分布. (a) 制御なし, (b) 位相シフト信号を与えた場合.
粒子群のカオス的挙動を定量評価するため,リアプノフ指数を計算した.これは,初期の微小差異の指数的乖離度を表し,次式で定義される.
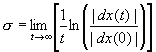
ここで, t は時間を表し, | dx (0) | および | dx ( t ) | は時刻 0 および t における2粒子間距離である. σが正の値をとれば,粒子間距離は | dx ( t ) |~| dx (0) |exp( σt ) で表されるように指数的に増加する.図 5 に,制御信号の周波数( St )に対する最大リアプノフ指数を示す.水平な実線は電磁力を与えない場合の値であるが,2次元の層流は非カオス的であるため,ほぼ 0 となる.一方,位相シフト信号を与えた場合, St =8 の付近で 0.3~0.4 のピークをとる.この周波数領域では,粒子群が図 4 に示されるようなカオス的挙動を示す.このとき,磁気ビーズの細胞への付着確率が増加することもシミュレーションによって確かめた [4] .
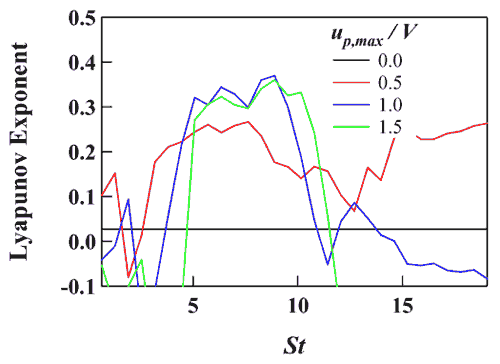
図5.制御ストローハル数に対するリアプノフ指数
3.マイクロデバイスの評価
図6に,実際に製作した蛇行流路デバイスの写真を示す.サイズは図2と同様で,流路深さ35µm,電極幅と電極間距離はともに40µmである.図中,流路の下半分には磁性粒子を含む純水が,上半分には何も含まない純水が並行に流れている.ここで,バルク流量は100nL/min,磁性粒子の体積濃度は1.7%である.図に見られるように,磁力による擾乱がない場合は,粒子拡散は起こらず,粒子群の境界面が下流に至るまで明瞭に観察される.
位相シフト信号を与えた場合の,混合過程の様子(動画)を図7に示す.初期状態(電磁力が与えられる前)では,流路の下半分において粒子密度が高くなっている.位相シフト信号が与えられると,粒子群は流路全域で繰り返し引き伸ばし・折り畳みの作用を受け,複雑なパターンを示しつつ攪拌される.下流では,磁性粒子は流路全体に均一に広がり,良好な混合状態が得られる様子が確認される.

図6.シリコン基板上に製作された蛇行形状流路およびマイクロ電極群.
画像粒子追跡流速計(Particle Tracking Velocimetry, PTV)を用いて,磁性粒子の運動が,シミュレーション結果と同様なカオス的挙動を示すことも確認された[5].

図7.マイクロ流路中での磁気ビーズの混合の様子(動画:クリックすると再生 3.5MB).
4.おわりに
磁気ビーズを用いたセルソーターの開発を目的として,ビーズを効率よく攪拌するためのマイクロ混合器を設計・製作した.マイクロ電極群および流路をチップ上に集積化し,電極群によって発生する変動磁場によって,磁気ビーズを操作可能であることを示した.また,良好な混合状態を実現するため,2次元の数値シミュレーションを行い,カオス理論に基づいた新しい混合手法を提案した.本手法は,電磁力のみでなく,静電力や誘電力などほかの制御外力を利用した場合にも応用可能であり,マイクロ TAS アプリケーションにおける粒子や生体分子,細胞などの能動的混合手法として汎用性の高いものである.
参考文献
[1] 日本エム・イー学会雑誌BME,「特集:マイクロ化学デバイスは医療を進化させるか?」,Vol. 15, No. 10, 2001.
[2] Ottino, J. M., “The Kinematics of Mixing: Stretching, Chaos, and Transport,” Cambridge University Press, 1989.
[3] Sinclair, B., “To Bead or Not to Bead: Applications of Magnetic Bead Technology,” The Scientist 12(13), pp. 17-20, 1998.
[4] 鈴木宏明,笠木伸英,Ho., C. M.,「磁性粒子を利用したカオス的マイクロ混合器」,日本機械学会論文集B編,69B, No. 688, 2003, pp. 2626-2632.
[5] Suzuki, H., Ho, C. M., Kasagi, N., “A Chaotic Mixer for Magnetic-Bead Based Micro Cell Sorter,” J. MicroElectroMechanical Systems, 13(5), 2004, pp. 779-790.

