流れ 2004年8月号 目次
― 特集:流体情報と融合研究 ―
| リンク一覧にもどる | |
流れの最適化とソフトコンピューティング
 東北大学流体科学研究所 流体融合研究センター 大林 茂 |
1. はじめに
数値流体力学(CFD)が設計現場で受け入れられるにつれ,性能向上・設計期間短縮など設計最適化への期待が高まっている.このような機運を受けて,CFDと最適化法を組み合わせた研究が最近学会などでも盛んに発表されるようになってきた.
しかし,与えられた流れの最適化問題が解けることと,それが設計に役立つことの間には,大きなギャップがある.流れの最適化は,多くの場合形状最適化に帰着する.形状最適化の解は,与えられた仮定のもとに目的関数が極値をとる1個の形状として与えられる.我々はその形状がどういう性能を持っているかという数値を得るが,その形状を異なる仮定や異なる目的関数のもとで用いることはできない.いわば個々のケースを積み重ねることはできても,それを知識として一般化し,他のケースに適用することはできない.
そこで本稿では,最適化を設計に役立てるとはどういうことかを考察し,ソフトコンピューティングの役割について議論する.
2. 設計とアブダクション
流体設計とは,要求を実現する形状を見出す一種の逆問題である.非常に単純化すると,我々は,簡単な形状にどのような流体力が発生するかという問題について限られた知識を持っており,これをもとに要求を満たす形状はどうあるべきかという問題の答えを予想する.この行為は,不完全な知識からの推論と位置づけることができ,アブダクションと呼ばれる.アブダクションとはパースによって導入された概念で,説明的な仮説を形成する過程(創造的洞察)であり,演繹や帰納に先立つ最も基礎的な推論の型である[1].設計という行為の核心部分で,アブダクションが重要な役割を果たすと考えられている[2].
そこで最適化が設計の役に立つということは,設計者のアブダクションに役立つということであると考えられる.アブダクションに役立つには,さまざまな仮説を思いつくような「仕掛け」が必要である.仮説とは,たとえばさまざまな観察結果にある「パターン」を見出すことである.このことはアブダクションの「仕掛け」としての「可視化」の重要性を示唆している.
再び流体問題に戻って,形状をパラメータ表現して流体性能を最適化することを考えてみよう.この場合,形状パラメータが設計変数であり,これに対して流体性能がどのような応答をするかということが完全に分かっていれば,最適化はほぼ自明である.たとえば,一変数xに対して応答yがあり,y = f(x) が与えられているならば,x-yのグラフを見れば(すなわち「可視化」すれば),応答の挙動や極値の存在はすぐに確認できる.一方,流体設計の難しさは,変数xが100以上の次元にもなるということと,関数fを求めるために流体の支配方程式を解かなければならないということである.つまり流体設計では,電卓をたたくような計算で単純なグラフを書いて応答を確認することができない.このことから,シミュレーションにより高次の設計空間(x,y)の構造を「可視化」することができると,設計者は最適解を予想する(!)ことができ,アブダクションに役立つと考えられる.すなわち,「設計空間の構造化と可視化」が「仕掛け」として重要である.
ここで,「設計空間の構造化と可視化」なしに,設計問題に最適な流体性能を与える形状パラメータのセットが与えられた場合を考えてみよう.その数値自体は最適解そのものであって,最適解を予想させるものではないので,アブダクションに役立たない.すなわち,最適解そのものは設計者の役に立たない.もちろん,その解が設計空間のどこにあるか,そのまわりの応答はどうなっているかという感度情報などの追加的な考察により,最適解近傍をさらに解析することによって,その情報をアブダクションに役立てることは可能である.それは,最適解が分かったあとで,その近傍の「設計空間の構造化と可視化」を行っていることに相当する.
では,高次元の「設計空間の構造化と可視化」を行い,設計者のアブダクションに役立てる手法は何であろうか?筆者は,それが複雑システムの解明に役立つソフトコンピューティングであると考える.
3. ソフトコンピューティング
ソフトコンピューティングは,決定論的な数学に基づくハードコンピューティングに対比する概念であり,ファジー・ニューロ・EA(進化的アルゴリズム)・確率推論等からなる.これらのソフトコンピューティング技法は,知的システムの構築や複雑システムの理解に用いられ,知的情報処理,知識抽出,データマイニング等への応用が期待されている.
3.1 多目的進化的計算法
筆者らは,EAが活躍する問題として多目的最適化を大きく取り上げてきた[3].多目的最適化問題の解は,もとの問題を何らかの工夫により単一目的の問題に変換するというスカラー化手法により,しばしば求められてきた.しかし,スカラー化による単一の最適解を求めても,情報としては不十分である.また,スカラー化で解を求められるのはパレート面が単純な凸形状である場合に限られるし,スカラー化の重みを調節して望みの解を得ることも決して容易ではない.
多目的最適化では「パレート最適解」という概念がある.パレート最適解とは,ある目的関数の値を改善するためには少なくとも1つの他の目的関数の値を改悪せざるを得ない解のことであり,目的関数間のトレードオフに関して最適な解の集合を形成することになる.ここで,複数の個体の発生により多点探索を行うというEAの特徴を考慮すると,適応度をパレート最適性で評価すれば,多数のパレート最適解を同時に求めることが可能であることに気付く.集団の個体がパレート集合になるべく一様に分布するような遺伝的操作を加味しながら進化をさせることができるのである.進化的な計算法では,これまでの単純EAとほぼ同様な関数評価の回数で,パレート解を同時に多数求めることができる.
多数のパレート解を一度に求めることにより,近似的なパレート集合が得られると,この集合からさまざまなトレードオフ情報を引き出すことができる.2目的の最小化問題を例にとり,目的関数空間におけるパレート面の位置と形状について考えてみよう(Fig.1).パレート面は曲線となる.その端は極限パレート解と呼ばれ,単目的の最適解に相当する.単目的の最適解は定性的に理解しやすいため,進化計算で得られた近似パレート集合が妥当なものか判断する目安となる.また,曲線の傾きはトレードオフそのものを表しており,傾きが極端に立っていたり寝ていたりする領域では,一方をほんの少し妥協すれば他方を大きく改善できる.パレート面は多くの工学問題で凸となるが,これは極限パレート解の単純平均をとるより,2目的を同時に最適化する方が良い性能を得られることを表している.逆に凹になるということは,極限パレート解の平均が実行不能解であるということになり,この2目的を同時に最適化することが大変難しい問題であることを示唆している.
このようにパレート面を可視化するということは,設計空間について多くの情報を与え,アブダクションに役立つと考えられる.しかし,Fig.1のようなグラフによる可視化が可能なのは,目的関数が2目的か,せいぜい3目的の場合であり,4目的以上の多目的最適化問題を解いたとしても,その結果を設計者が理解しやすいように可視化することは容易ではない.ここでは,多目的進化的計算法を設計空間構造化のツールと位置づけ,次に可視化法を考えてみよう.
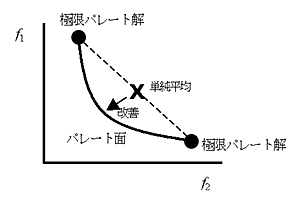
Fig. 1 Schematic view of Pareto front
3.2自己組織化マップ
筆者らは,高次元空間の可視化法として,自己組織化マップ(Self-Organizing Map, SOM)を用いている[4].SOMは,提案者の名前を取ってコホネンネットとも呼ばれ,近年脚光を浴びているデータマイニングの一手法である.SOM は,教師なし学習のアルゴリズムを用いるフィードフォーワード型のニューラルネットモデルである.
SOMは,入力層と出力層の2層からなり,隠れ層はない.第2層を構成するユニットはあらかじめ平面座標を持っている.第1層に提示された情報はすべて第2層に提示され,第2層のユニットは入力情報にどれだけ似ているかを競争する.競争の結果選ばれた勝者ユニットは,重み付けが更新されてさらに入力に近づく.また,その近傍ユニットも近さに応じて重みを更新される.こうして隣り合うユニットは似たような重みを持つようになり,第2層に新たな位相が形作られる.通常この第2層(出力層)をSOMの結果として図示する.
SOMは,我々が直感的に理解している地図とは異なる.通常の地図では,方角(座標軸)があり,距離(ユークリッド距離)が定義されている.SOMには,方向性がなくユークリッド距離も定義されていない.隣り合うユニットは類似度が高いが,n個離れたら類似度が1/nになるわけではないし,異なるユニットはまわりのユニットに対して異なる近さを持っている.その代わり,SOMは多次元情報を2次元に折りたたんで表現できる.すなわち,SOMを用いると多次元データの可視化ができる.
たとえば4目的最適化の近似パレート集合から目的関数空間のSOMを作る場合(Fig.2),各ユニットは4つの目的関数値に対応して4次元ベクトルを持っている.ユニットの類似度は,この4次元ベクトルのユークリッド距離で測られる.できあがったSOM上で,ユニットの各成分(4つの目的関数値)について,4つの等高線図を作成することができる.その図を比較すると,トレードオフの有無などパレート面の構造が確認できる.
SOMによる可視化には,さらにクラスタリングを組み合わせることができる.もともとSOMでは近傍ユニットが似たもの同士になるので,SOM上でクラスタリングを行うことは,もとデータからクラスタリングを行うよりはるかに容易である.クラスタの特徴は,各成分のトレードオフなどから見出すことができる.このようにSOMは高次元の可視化ツールと位置づけることができる.
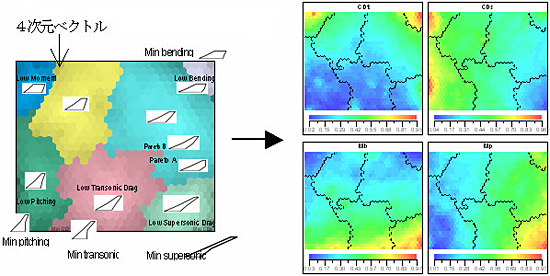
Fig. 2 SOM for 4-objective design optimization
以上より,ソフトコンピューティングの代表的手法であるEAとSOMの組み合わせが,高次元の「設計空間の構造化と可視化」のツールとなり,設計問題の多様で俯瞰的な理解を促し,設計者のアブダクションに役立つことが期待される.また,今後は流体と構造など多分野統合設計への適用も期待される.
4 文献
[1] デイヴィス,パースの認識論,産業図書,1990.
[2] 冨山哲男,設計の理論,現代工学の基礎15,岩波書店,2002.
[3] S. Obayashi, D. Sasaki, and A. Oyama, "Finding Tradeoffs by Using Multiobjective Optimization Algorithms," Transactions of the Japan Society for Aeronautical and Space Sciences, Vol. 47, No. 155, pp. 51-58, May 2004.
[4] コホネン,自己組織化マップ,シュプリンガー・フェアラーク東京,1996.

