流れ　2006年9月号　目次

―　特集：　風洞・水槽で流れを造る　― ACサーボモータでファンを駆動する風洞による風速風向変動の生成 野村卓史（日本大学理工学部） 乱流風洞による実験的研究の可能性 関下信正（豊橋技術科学大学） 風車の風洞実験 前田太佳夫（三重大学），鎌田泰成（三重大学） インデックスマッチングを利用した流れの可視化実験 西野耕一（横浜国立大学大学院工学研究院） 編集後記 磯　良行（石川島播磨重工），安藤　俊剛（三重大学）， 東村　哲志（シーディー・アダプコ・ジャパン），辻　知宏（高知工科大学） 　｜　リンク一覧にもどる　｜

 

乱流風洞による実験的研究の可能性

関下信正 豊橋技術科学大学

1. 　はじめに

　現在，風洞は航空分野をはじめ，自動車，鉄道，建築，環境など様々な分野で使用され，風洞実験によって，輸送機器の性能向上や空力騒音の低減，高層ビルや超大橋の耐風や風環境の評価，煙突からの熱物質拡散の予測などに役立っている．

　風洞 ( 図 1 ⁽¹⁾ ) は，室内に空気の流れを造る実験装置であり，流路の形状と送風機の位置によって回流式，吹き出し式，吸い込み式風洞に大きく分類できる．基本的には送風機とダクトで構成される風洞は，一見，単純な装置のように見えるが，理想的な流れ場を実現するために，様々な工夫が凝らされており，境界層や物体後流などの基礎的な風洞実験では，速度変動を極力抑えた良質な流れ場の実現に注意が払われる．航空や自動車用の風洞実験では，実機と同様の流速 ( または，レイノルズ数 Re ) を実現することはもちろんのこと，航空機の離着陸時の空力特性や車両の走行実験では，地面効果を再現するためにムービングベルトなどの補助装置が用いられる．また，都市や超大橋の風環境実験では，精巧な模型が測定胴中に設置され，大気と同様の特性を有する風を風洞中に再現する努力が払われる．

　風洞中に実験対象を設置して風を吹かせば実験データをとりあえず取れるが，信頼性が高く良い結果を得るためには，単に幾何学的レイノルズ数を合わせるだけでなく，対象としている実際の現象と類似した流れ場を風洞中に可能な限り忠実に再現することが大切である．上述したように，様々な分野の流体力学的問題に対して風洞実験が行われているが，ここでは，大気拡散やビル風などの大気中で生じる乱流現象、および、乱流の統計的性質の解明などに用いられる乱流風洞について詳述したい．

　なお，風洞実験に関する詳細な文献としては， Rae & Pope ⁽²⁾ , 谷・小橋・佐藤 ⁽³⁾ , 日本流体力学会 ⁽¹⁾ , Tavoularis ⁽⁴⁾ などを，乱流現象の風洞実験でよく使用される熱線計測に関しては Perry ⁽⁵⁾ ， Bruun ⁽⁶⁾ を参照されたい．

 

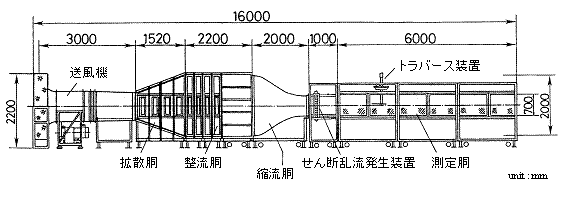
図 1 　大気乱流風洞 ⁽¹⁾ ( 吹出し型 )
( 豊橋技術科学大学 )

 

2. 　従来の乱流風洞

　一般的な風洞実験では，送風機やコナーベーン ( 変流板 ) などによって発生した速度の変動 ( 乱れ ) を極力抑えた良質な気流を得る工夫がなされているが，それとは反対に，乱流風洞では，大小様々なスケールの乱流渦を誘起し，かつ，大きなエネルギーを持った大規模渦を含んだ乱流場の実現が求められる．簡単な例を挙げると，前者が ”1/f ゆらぎ ” 機能のない扇風機の風，後者が台風の風に対応する．

　風洞中に乱流を形成する場合，一般的には，乱流格子 (turbulence grid, 図 2) ⁽⁷⁾ が使用されてきた．これは，丸棒や角棒を格子状に組んだものを風洞測定胴上流に設置することにより，断面内で平均速度が一定である一様乱流場を形成することができる．この手法は，比較的に簡単な構造の補助装置 ( 乱流格子 ) で乱流場を風洞中に形成できる．ただし，乱流格子では，大きなエネルギーを持った大きな乱流渦を誘起することが難しく ( 図 3 ⁽⁸⁾-⁽¹⁰⁾ ) ，特性速度 ( 乱流エネルギーを 1/3 して平方根を取った値 ) とテイラーのマイクロスケールに基づく乱流レイノルズ数が 100 程度の乱流しか通常規模の風洞では実現することができない ( 大気の乱流レイノルズ数は 1000 以上 ) ．

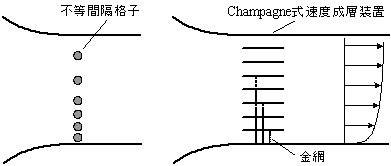
　さらに，乱流風洞にはもう一つの機能が求められ，大気中の乱流現象を風洞中に再現する場合などでは，平均速度勾配の制御も必要である．大気境界層型の速度分布を形成する手法として，一般的には，測定胴床面に敷きつめた粗度 (roughness elements, 図 4) ，および，測定胴最上流に設置された三角錐形のスパイヤー (high-drag strakes) ⁽²⁾ が多用される．スパイヤーを回転させることによって，より強い乱れを得る手法も行われている ⁽¹¹⁾ ．その他に，高さ方向に速度勾配が一定な一様せん断流や境界層など，任意の速度分布を形成する風洞補助装置として，不等間隔格子 ⁽¹²⁾ ， Champagne 式速度成層装置 ⁽¹³⁾ ，佐藤式速度成層装置 ⁽¹⁴⁾ などがある．これらは測定胴上流に設置され，不等間隔格子 ( 図 5) は，細い棒を高さ方向に不等間隔に並べ，高さ方向に流路面積を変化させることによって，速度分布を制御する手法である． Champagne 式速度成層装置 ( 図 5) は，流路を数～数十段に分割して各段に金網などを入れることによって，各流路の流体抵抗を変え，任意の速度分布を得るものである．佐藤式速度成層装置 ( 図 5) は，高さ 50mm 幅 10mm の開口部が沢山ある 2 枚の板をずらすことによって，流量を変化させて高さ方向に速度勾配を形成できる．

 

図 2 　乱流格子

 

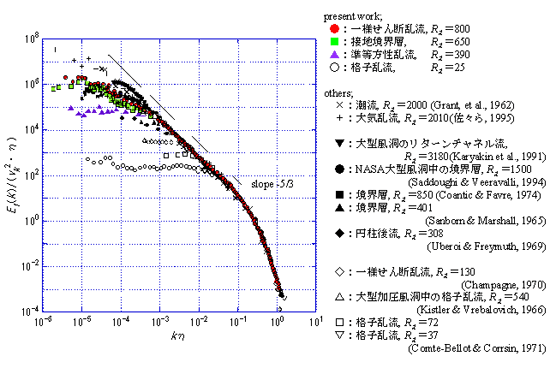
図 3 　エネルギースペクトルによる風洞乱流と自然界の乱流との比較
Saddoughi & Veeravali ⁽⁸⁾ が整理した結果に，潮流 ⁽⁹⁾ ，大気乱流 ⁽¹⁰⁾ ，せん断乱流
発生装置 (3 ・ 3 節 ) によって形成された乱流場のスペクトルを加えたもの

 

 

図 4 　粗度とスパイヤー

 

佐藤式速度成層装置 (14)

図 5 　様々な速度成層装置

 

3. 　高レイノルズ数乱流を実現する試み

　前節で乱流格子を紹介したが，大気乱流のように，より大きな乱流レイノルズ数の乱流場を得るために様々な工夫 ( 図 6) がなされ，乱流格子と噴流を組み合わせた噴流格子 ⁽¹⁵⁾,⁽¹⁶⁾ による実験や，振動翼 ^(17)(18) などの風洞補助置が試されている．高レイノルズ数乱流を形成した実験的研究の中でも，注目すべき成果を以下で紹介する．

 

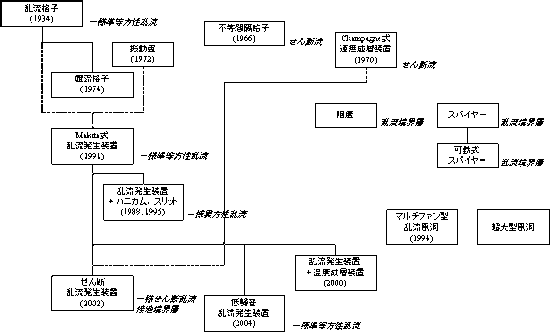
図 6 　高レイノルズ数乱流の実現を目指して開発された風洞補助装置

 

3 ・ 1 　超大型風洞

　Kolmogorov の慣性小領域 ⁽¹⁹⁾ を風洞乱流で明確に示した最初の研究者は Kistler & Vrebalovich ⁽²⁰⁾ であり，彼らは大型風洞を 4 気圧に加圧して乱流格子で一様準等方性乱流場を形成し，乱流レイノルズ数 669 の高レイノルズ数乱流を実現した．これは，幾何学的レイノルズ数で 1,000,000 に相当する．

　近年では，乱流の統計的性質，特に， Kolmogorov の普遍平衡理論 ⁽¹⁹⁾ の検証，および，乱流場の微細構造 ⁽²¹⁾ を調べるために，超大型大型風洞が使用されている． Gagne ら ⁽²²⁾ は，フランス ONERA にある回流風洞のリターン流路 ( 直径 24m, 長さ 150m) において乱流レイノルズ数 2,720 ， Kuznetsov ら ⁽²³⁾ は，超大型風洞のノズル ( 長軸 24m, 短軸 14m) を用いて乱流レイノルズ数 1,660 ， Saddoughi & Veeravalli ⁽⁸⁾ は NASA Ames Research Center の超大型風洞 ( 図 7) の測定胴天井に発達した乱流境界層を計測し，乱流レイノルズ数 14,500 の乱流場を実現している．これらの乱流の速度変動から得られるエネルギースペクトル ( 図 3) を見ると，低波数 ( 大きな乱流渦 ) のエネルギーレベルが大きく，その結果，図中で－ 5/3 の勾配を有する Kolmogorov の慣性小領域が明確に存在していることからも，大気や潮流と同様な大規模乱流場であることがわかる．ただし，超大型風洞の場合には経済性や運用面に難点がある．

 

図 7 　超大型風洞 ⁽⁸⁾ (80×120ft 測定胴の空気取り込み口 )

( NASA Ames Research Center )

 

3 ・ 2 　マルチファン型乱流風洞

　これまで説明した乱流風洞とは全く別のアイディアで開発されたものが，小園・西ら ⁽²⁴⁾ による マルチファン型乱流風洞 ( 図 8) である．この風洞は， 99 個 ( 横に 9 個，縦に 11 段 ) の AC サーボモータに直付けされたファンが空気取り入れ口にあり，それらのファンが個別にコンピュータ制御される．野外で計測した速度変動をカルマンの式を用いて逆フーリエ変換して風洞制御用時系列データを作成し，それに基づいてマルチファンを制御することによって，自然風を測定胴 ( 幅 2565mm, 高さ 1800mm) 中に再現することが可能である．この風洞は，特に，突風などの風環境試験に適している．

 

図 8 　マルチファン型乱流風洞 ⁽²⁴⁾
( 宮崎大学 )

 

3 ・ 3 　せん断乱流発生装置

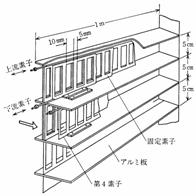
　大規模乱流場の統計的性質の解明と乱流理論の検証，さらに，大気中における様々な乱流現象の正確な実験的シミュレーションを行うために， Makita ^(25)(26) は せん断乱流発生装置 ( 図 9) を開発した．この装置は，上流側の速度形成部と下流側の乱流発生部で構成され，速度形成部は，上述した Champagne 式速度成層装置 (13) と同様な構造の成層装置である．乱流形成部は，縦横各 20 本の格子上の回転軸 ( 格子間隔 35mm) に，多数の攪拌翼が取り付けてある．各回転軸は外部のステッピングモータで個別に駆動され，一定回転速度で回転しながら，設定した回転範囲β内でランダムに反転する．この装置では，攪拌翼が気流を掻き乱す作用のほかに，攪拌翼や回転軸の後流や，攪拌翼がランダムに回転して時間的に開口部が変化することによって生じる噴流の効果などが混ざり合って，高レイノルズ数乱流を形成することができる．その結果，エネルギースペクトル ( 図 3) において，低波数 ( 大きな乱流渦 ) に大きなエネルギーを注入でき，広い慣性小領域が存在し，大気乱流や潮流のスペクトル分布に匹敵している．なお，この装置の一つの特徴として，設定する攪拌翼の平均迎え角αと回転範囲β ( 図 9) を変えることによって，同一平均流速でも異なる乱流レイノルズ数や異方度の乱流場を実現できる．

　蒔田の研究グループは，この装置を用いて Kolmogorov の普遍平衡理論の検証 ^(27)(28) ，一様等方性乱流場の減衰特性 ⁽²⁹⁾ ，一様異方性乱流場の等方化過程 ^{(30) (31)} などの基礎的な乱流研究をはじめ，連続点源からの粒子拡散 ⁽³²⁾ ，大気乱流境界層の実験的シミュレーション ⁽³³⁾ などの応用実験も行ってきた．粒子拡散の実験 ( 図 10) では，通常規模の風洞でプルームの蛇行現象を初めて実現し，せん断乱流発生装置によって誘起された大規模渦が乱流拡散に与える重要性を明らかにした．さらに，この乱流発生装置は， 温度成層装置と組み合わせた風洞 ⁽³⁴⁾ ，および， 低騒音乱流風洞 ⁽³⁵⁾ などへ発展されている．この装置の有効性が国内外で認められ，近年では， Makita 式乱流発生装置を基にした乱流風洞が Cornell 大学 ⁽³⁶⁾ や電力中央研究所 ⁽³⁷⁾ などでも建造され，乱流の風洞実験に使用されている．

 

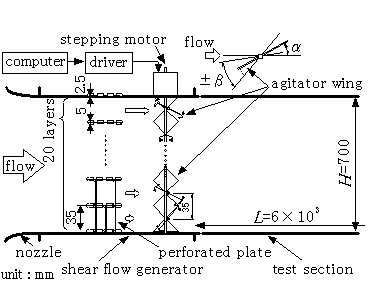
図 9 　せん断乱流発生装置 ⁽³³⁾
( 豊橋技術科学大学 )

 

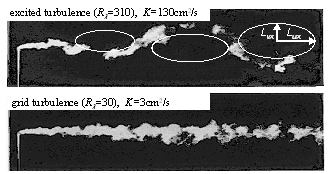
図 10 　一様大規模乱流場と一様格子乱流場中における連続点源からの粒子拡散の比較 ⁽³²⁾
写真中の白丸は誘起されたインテグラルスケールの大きさ

 

 

4. おわりに

　“ 乱流の本質とはなにか ” ということを十分に考えた上で独自の乱流風洞を開発することによって，観察したい現象をできるだけ忠実に風洞中に再現するとともに，緻密な計測を行うことは乱流実験においてとても大切なことである．そのためには，創意工夫を凝らした風洞の開発が必要不可欠であり，独創的な風洞実験や計測技術の発展によって新しい発見や実験データが提供され，理論的な研究や数値計算とともに乱流研究が発展することを願っている．

 

参考文献

(1)	日本流体力学会 , 流体ハンドブック第 2 版 (1998), p1172, 丸善 .
(2)	Rae, W.H, & Pope, A, Low-Speed Wind Tunnel Testing (1984), John Wiley & Sons.
(3)	谷・小橋・佐藤 , 流体力学実験法 (1977), p14, 岩波 .
(4)	Tavoularis, S., Measurement in Fluid Mechanics (2005), p154, Cambridge University Press.
(5)	Perry, A.E., Hot-wire anemometry, (1982), Clarendon Press, Oxford .
(6)	Bruun, H.H., Hot-Wire Anemometry (1995), Oxford University Press.
(7)	Simons, L.F., & Salter, C., Experimental investigation and analysis of the velocity variations, Proc. Roy . Soc. Ser. A, 415 (1934), p212.
(8)	Saddoughi, S.G. & Veeravalli, S.V., Local Isotropy in Turbulence Boundary Layers at High Reynolds Number, J. Fluid Mech., 268 (1994), p333.
(9)	Grant, H.L., Stewart, R.W. & Moilliet, A., Turbulence spectra from a tidal channel, J. Fluid Mech. 12 (1962), p241.
(10)	佐々・千葉・蒔田 , 接地境界層中の乱流微細構造に及ぼす安定度の影響 , 日本流体力学会第 27 回乱流シンポジウム講演論文集 (1995), p203.
(11)	Nagai, N., Wind tunnel modeling of hourly observed atmospheric diffusion by oscillating blade cascade, J. Wind Eng. Ind. Aero. 93 (2005), p99.
(12)	Rose, W.G., Results of an attempt to generate a homogeneous turbulent shear flow, J. Fluid Mech., 25 (1966), p97.
(13)	Champagne , F. H., Harris, V. G. & Corrsin, S., Experiments on nearly homogeneous turbulent shear flow, J. Fluid Mech., 41 (1970), p81.
(14)	佐藤・恩田・斉藤 , 東京大学宇宙航空研究所報告 , 9 (1973), p675.
(15)	Gad-el-Hak, M. & Corrsin, S., Measurements of the nearly isotropic turbulence behind a uniform jet grid, J. Fluid Mech. 62 (1974), p115.
(16)	Tassa, Y. & Kamotani, Y., Experiments on turbulence behind a grid with jet injection in downstream and upstreamdirection, Phys. of Fluids, 18 (1975) p411.
(17)	Ling, S.C. & Wan, C.A., Decay of isotropic turbulence generated by mechanically agitated gird, Phys. of Fluids, 15 (1972), p1363.
(18)	斉藤・佐藤 , 大気の乱れを風洞の中に作る一方法 , 乱流シンポジウム講演論文集 (1974), p103.
(19)	Kolmogorov, A.N., The local structure of turbulence in incompressible viscous fluid for very large Reynolds number, Dokl. Acad. Nauk SSSR, 30 (1941), p9 (reprinted in Proc. R. Soc. Lond., A 434, (1991), 9).
(20)	Kistler, A.L. & Vrevalovich, T., Grid turbulence at large Reynolds numbers, J. Fluid Mech., 26 (1966), p37.
(21)	Frish, U., Turbulence, (1995), p120, Cambridge University Press.
(22)	Gagne, Y., Hopfinger, E.J. & Frish, U., A New Universal Scaling for Fully Developed Turbulence, NATO ASI, 237 (1990), p315.
(23)	Kuznetsov, V.R., Praskovsky, A.A. & Sabelnikov, V.A., Fine-Scale Turbulence Structure of Intermittent Shear Flows, J. Fluid Mech., 243 (1992) p595.
(24)	小園・西・他 4 名 , マルチファン型大型風洞の開発 ( 一様アクティブ法により生成される乱流の特性 ), 機論 , B 70-690 (2004), p311.
(25)	蒔田・飯田・佐々 , 大規模乱流場の特性の評価 ( 第 4 報 , 乱流レイノルズ数と Kolmogorov 普遍定数について ), 機論 , B 54-505 (1988), p2333.
(26)	Makita, H., Realization of a large-scale turbulence field in a small wind tunnel, Fluid Dyna. Res., 8 (1991), p53.
(27)	蒔田・飯田 , 高レイノルズ数乱流場の統計的性質 ( 第 3 報 , 自己相似性と普遍平衡理論について ), 機論 , B 56-522 (1990), p351.
(28)	蒔田・関下 , 普遍平衡炉論の実験的検証 , 機論 , B 63-606, (1997), p544.
(29)	蒔田・関下 , 一様等方性乱流の減衰特性 , 機論 , B 62-594, (1996), p466.
(30)	蒔田・岩崎・飯田 , 軸対称異方性乱流場の実験的解析 , 機論 , B 54-505 (1988), p408.
(31)	蒔田・南 , 三次元異方性乱流場の減衰過程に関する実験的研究 , 機論 , B 61-581 (1995), p26.
(32)	蒔田・佐々・飯田・茂山 , 大気乱流拡散の実験的シミュレーション , 機論 , B 522 (1990), p388.
(33)	関下・蒔田・一郷・藤田 , 大気乱流境界層の実験的シミュレーション , 機論 ,B 68-665 (2002), p55.
(34)	Sassa, K., Matsunaga, S., & Makita, H., Buoyancy effect and universal structure of a stably stratified turbulence field, Advances in Turbulence VIII, (2000), p.291, International Center for National Methods in Engineering, Barcelona.
(35)	Iida, A., Morita, K., & Tanida, H., Effect of Incoming Flow Turbulence on Aerodynamic Noise from Automobiles, Review of Automotive Engineering, 27, 4 (2006).
(36)	Mydlarski, L. & Warhaft, Z. : Passive scalar statistics in high-Peclet-number gird turbulence, J. Fluid Mech., 358 (1998) 135.
(37)	Hattori, Y., Tsuji, T., Nagano, Y., & Tanaka, N., Effects of free stream turbulence on combined-convection boundary layer along a vertical heated plate, Proceeding of 4th International Symposium on Turbulence and Shear Flow Phenomena (2005), p989.