流れ　2008年9月号　目次

 

希薄気体流れのマルチスケール解析

松本洋一郎 東京大学 杵淵郁也 東京大学

1. はじめに

　希薄気体流れの数値解析には，ボルツマン方程式の確率解法であるモンテカルロ直接(direct simulation Monte Carlo, DSMC)法^[1,2]が広く用いられている．DSMC法により流れを正確に再現するためには，信頼性の高い分子間衝突モデルが必要であり，これまでに多数の研究がなされてきた．例えば，衝突断面積や散乱角度を決定するためには，variable hard sphere (VHS)モデル^[3]やvariable soft sphere (VSS)モデル^[4]が広く用いられている．また，衝突による分子の内部自由度間のエネルギー移動は，Borgnakke-Larsen (B-L)モデル^[5]やそれを拡張したモデル^[6-9]などによって与えられる．これらのモデルは比較的単純であり計算コストが低いという利点がある．ただし，これらのモデルを適用するためには，分子種ごとに経験的なパラメーターを与えなくてはならない．例えば，VHS/VSSモデルを用いるためには，粘性係数と拡散係数を広範囲の温度域にわたってあらかじめ知っておく必要がある．B-Lモデルでは，緩和衝突数を与える必要がある．これらの経験的パラメーターの多くは，熱平衡の仮定を基に算出されるものであり，希薄気体流れにおいて顕在化しやすい非平衡性の強い系に対して適用することが適切であるとは言い難い．また，半導体のchemical vapor deposition (CVD)プロセスなどでは多くの化学種が用いられており，そもそも必要な物性値が得られていないことも多い．このような場合には，解析の精度に関してはある程度妥協して，不確実性の大きいパラメーターを用いるか，あるいは剛体球モデルのように非常に単純なモデルを用いて計算を行なうといった方法を採らざるを得ない．このような困難を克服するためには，電子状態から分子運動，さらには熱流動現象を体系的に結び付ける数値解析手法であるマルチスケール解析が有効である．

 

2. マルチスケール解析

　希薄気体流れの流動構造は，分子の衝突過程と移動過程によって決定されている．衝突過程において分子間に働く力は，分子の電子状態を量子力学的に解析することで求められる．したがって，系に含まれる全ての電子・原子核について量子力学的に解析を行なえば，原理的には希薄気体流れを解くことができるのであるが，それは計算コストの面から非現実的である．そこで，最終的にマクロスケールの現象に影響を及ぼしている様々な空間・時間スケールにおける物理に対して，相互作用の無視できる領域ごとにスケールをうまく分離し，それぞれのスケール間をモデルによって合理的に接続することを考える．このようにすると，現実的な計算量の範囲内で，量子力学を出発点として合理的にマクロスケールの希薄気体流れを解析することが可能となる．このような手法がマルチスケール解析である．

希薄気体流れについてスケール間の分離を考えると，量子力学により記述される電子運動のスケール，古典力学により記述される分子衝突過程のスケール，ボルツマン方程式により記述される流れのスケールに分離できる(図1)．電子運動のスケールに対しては，相互作用する分子周りの電子状態を第一原理計算により求めて，分子間に働く力を算出する．そして，得られた結果を再現するように分子間ポテンシャルモデルを構築する．次に，分子衝突過程のスケールでは，構築したポテンシャルモデルを用いて古典軌道計算を行なうことで分子の二体間衝突過程を解析し，衝突断面積と分子間のエネルギー輸送に関する統計的な衝突モデルを構築する．最後に，このようにして構築した衝突モデルを用いてボルツマン方程式を数値的に解くことにより，マクロスケールの流れが解析できる．

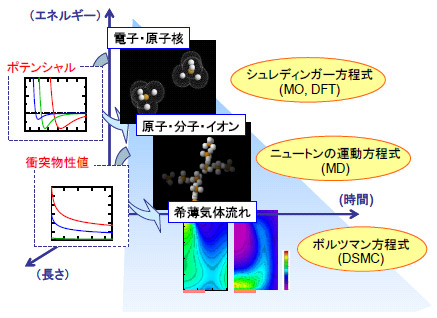
図1 希薄気体流れにおけるマルチスケール解析の概念^[11]

 

　 また，希薄気体流れでは，固体表面に衝突した気体分子の散乱挙動が流れ全体に大きな影響を及ぼすことが知られているが，同様の方法論に基づいて，高精度の表面散乱モデルを構築することも可能である^[10]．

　 以下ではマルチスケール解析を概観するために，半導体のCVDプロセスにおいて使用されているシラン(SiH₄)^[11,12]および工業的に広く用いられている気体である窒素(N₂)^[13]を対象とした解析をモデルケースとして取り上げる．

 

3. 分子間ポテンシャルモデルの構築

　多原子分子であるSiH₄間の分子間ポテンシャルは，距離のみではなく分子の相対的な向きに依存して大きく変化する．そこで，代表的な相対関係を抽出し，それらに対して重心間距離を変化させて分子間ポテンシャル平面を作成した．図2に代表的な相対関係と，それぞれの関係におけるポテンシャルエネルギーの様子を示す．このように異方性の強い複雑なポテンシャル平面を表現するために，各原子核間の二体ポテンシャルの線形和により表わされるサイト-サイトポテンシャルモデルを導入した．

図2 分子軌道法によるポテンシャルエネルギーの計算例^[11]

 

　 非経験的に第一原理から構築したポテンシャルモデルの妥当性を検証するために，SiH₄に関して実験的に求められている数少ない物性値である粘性係数を，構築したポテンシャルモデルを用いて古典的分子動力学法により算出した値と比較した(図3)．気体・液体の両方の状態に対して，構築したポテンシャルモデルにより物性値が良く再現できていることが確認できる．

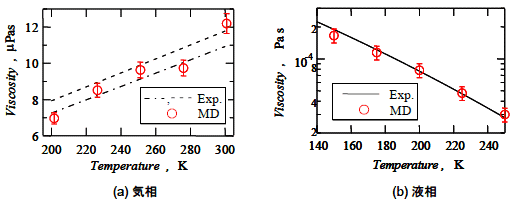
図3 粘性係数^[12]

 

4. 分子間衝突モデルの構築

　次に，上記で得られた分子間ポテンシャルモデルを用いて，SiH₄間の分子間衝突の解析を行なった．計算には古典分子動力学法を適用した．初期の相対速度，衝突係数，衝突エネルギーを様々に変化させた衝突計算を多数行ない，統計的解析から衝突断面積，散乱角分布，エネルギー緩和確率モデルを構築した．図4に計算から得られた全衝突断面積と散乱角分布の一例を示す．解析の結果から，全衝突断面積は並進エネルギーのみによってスケーリングできることがわかった．また，散乱角は，単原子分子に対する古典散乱理論の結果を中心とする正規分布に従うことが明らかとなった．

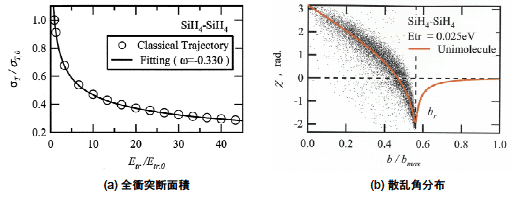
図4 全衝突断面積および散乱角分布^[11]

　 また，分子衝突による内部自由度間のエネルギー移動に関してもモデルが構築できる． N₂間の衝突による並進・回転エネルギーの変化について解析を行なった例を図5に示す．ここでは振動運動は凍結しているものとみなしている．解析の結果から得られた統計量を基にして，エネルギー交換モデルが構築される．構築したモデルを用いたDSMC法による計算により，衝撃波内部の並進・回転温度分布が再現されることが確認できた．

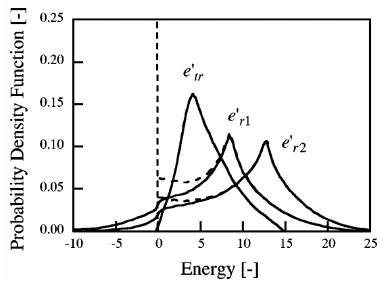
図5 衝突後の並進・回転エネルギー分布(N₂)^[13]

 

5. まとめ

　本稿では，希薄気体流れのマルチスケール解析について紹介した．流れの現象をスケールごとに分離し，それぞれのスケール間を合理的に接合することにより，マクロスケールの流れの解析にミクロスケールにおける現象の影響を正しく反映させることが可能となる．この手法は経験的なパラメーターを必要とせず，さらに非平衡性の強い系も取り扱うことが可能である．

 

参考文献

[1]	K. Nanbu, J. Phys. Soc. Jpn. 49, 2042 (1980).
[2]	G. A. Bird, Molecular Gas Dynamics and the Direct Simulation of Gas Flows, Clarendon Press, Oxford (1994).
[3]	G. A. Bird, Prog. Aeronaut. Astronaut. 74, 239 (1981).
[4]	K. Koura and H. Matsumoto, Phys. Fluids A 3, 2459 (1991).
[5]	C. Borgnakke and P. S. Larsen, J. Comput. Phys. 18, 405 (1975).
[6]	B. L. Hass, D. B. Hash, G. A. Bird, F. E. Lumplin and H. A. Hassan, Phys. Fluids 6, 2191 (1994).
[7]	I. D. Boyd, Phys. Fluids A 5, 2278 (1993).
[8]	I. D. Boyd, Phys. Fluids A 2, 447 (1990).
[9]	F. Bergemann and I. D. Boyd, Prog. Aeronaut. Astronaut. 158, 174 (1994).
[10]	N. Yamanishi, Y. Matsumoto and K. Shobatake, Phys. Fluids 11, 3540 (1999).
[11]	Y. Sakiyama, S. Takagi and Y. Matsumoto, Phys. Fluids 16, 1620 (2004).
[12]	Y. Sakiyama, S. Takagi and Y. Matsumoto, J. Chem. Phys. 122, 234501 (2005).
[13]	T. Tokumasu and Y. Matsumoto, Phys. Fluids 11, 1907 (1999).