流れ　2008年9月号　目次

 

ダイヤモンド膜摺動実験における揚力発生機構の分子気体力学的考察

米村 茂 東北大学 山口雅志 東北大学 竹野貴法 東北大学 三木寛之 東北大学 高木敏行 東北大学

1. はじめに

　近年の化学気相合成法の進歩により，ダイヤモンド薄膜を作製することができるようになった．バルクのダイヤモンドはその劈開面において非常に低い摩擦係数を示すことが知られており，気相からの合成によって低摩擦を示すダイヤモンド膜を作製できれば，工業的な応用可能性が非常に大きくなる．例えば，Eldemirら⁽¹⁾は非常に滑らかな表面を有するナノクリスタルダイヤモンド(Nanocrystalline Diamond: NCD)薄膜を気相より作製することに成功し，その摩擦係数が窒素雰囲気下で0.1を下回ることを報告している．さらに，Takenoら⁽²⁾は部分的に研磨したバラス型ダイヤモンド膜において，その摩擦係数が表面粗さに依存することを示し，ダイヤモンド膜同士の摩擦係数が組み合わせによっては大気環境中で0.07を示す事を報告している．しかしながら，これらの実験は主に低摺動速度における実験的結果である．ダイヤモンド膜の高硬度や耐摩耗性は，低摩擦特性とともにダイヤモンド膜の特性としてよく知られている．これらの機械的，トライボロジー特性により，特に摩耗の激しい高負荷・高摺動速度環境において低摩擦が期待できるが，このような条件における実験的事実はこれまでに殆ど報告されていない．

　 Nakamoriら^(3,4)は部分研磨したダイヤモンド膜をスライダーの底面に貼り付け，図1に示すように回転金属板上で高速度で摺動させる実験を行った．この実験では，図2に示すように摺動速度の上昇とともに摩擦係数が劇的に減少した．摩擦係数の急激な遷移を起こす速度付近では，低摩擦へ遷移した後に摺動音が発生しなかったことから，潤滑形式が境界潤滑から気体潤滑へと遷移したと考えられる．摩擦係数の急激な低下の後，固体面間の接触はなく，両面間に空気が挟まれクッションの役割をすると考えられるが，そのメカニズムは明らかではなかった．本研究では両面間に挟まれた空気の流れの数値シミュレーションを行うことにより，ダイヤモンド膜浮上のメカニズムを調べることを目的にしている．

　 図3に部分研磨されたダイヤモンド膜の表面の走査型電子顕微鏡(Scanning Electron Microscope: SEM)像を示している．ダイヤモンド膜同士を共擦りすることにより研磨しているが，溝を完全になくなるほど研磨した場合よりも，ある程度溝を残した場合の方が低摩擦となった．Nakamoriらの実験^(3,4)で用いられたダイヤモンド膜表面の算術平均粗さは0.28 µmから0.57 µmである．また両面間の距離が表面粗さに比べて大きい場合，平行平板間のクエット流れに近くなる．ダイヤモンド膜が浮上するためには両面間の空気の圧力が高くなりスライダーを支える必要があるが，クエット流れでは圧力は発生しないため，表面粗さと同程度に両面間の距離も小さいと考えられる．つまり両面間に挟まれた流れの代表長さLは1 µm程度あるいはそれ以下であると考えられる．この実験は大気中で行われており，分子の平均自由行程λは0.065 µmである．平均自由行程λと流れの代表長さLの比で定義されるクヌッセン数Kn=λ/Lは0.1程度以上の大きさとなると考えられ，このような流れを連続体として取り扱うことはできず，支配方程式はナビエ・ストークス方程式ではなく，ボルツマン方程式となる．そこで本研究ではボルツマン方程式の確率解法であるDSMC法^(5,6,7)による数値シミュレーションにより，両面間の流れを再現し，スライダーが浮上するメカニズムを考察する．

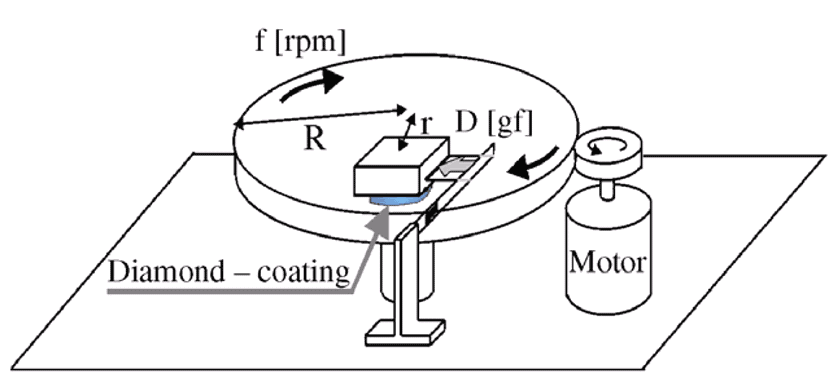
図1 ダイヤモンド膜の摩擦係数計測実験

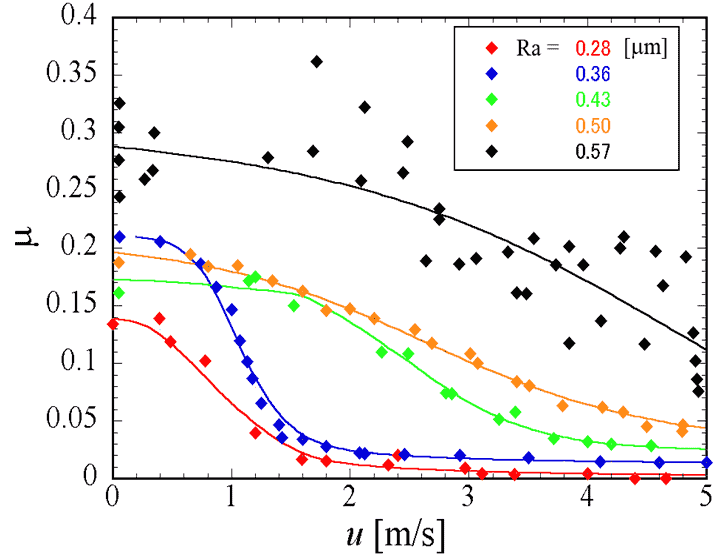
図2 摩擦係数と摺動速度の関係

図3 部分研磨されたダイヤモンド膜表面

2. DSMCシミュレーション

　 図4に計算領域を示す．本計算ではダイヤモンド膜と回転金属板で挟まれた狭い領域の空気の流れを2次元流れとして模擬する．上面はダイヤモンド膜を表し，凹部はダイヤモンド膜表面に残された溝を表す．下面は金属板を表し，右方向に速度uで移動している．左右両端の境界には周期境界条件を適用しており，右側境界から出た分子は左側境界から同じ速度で入射する．このため，計算領域内の分子数は変化しない．本計算では上面のダイヤモンド膜と対向面の金属板との間の距離は時間的に変化しないと仮定し，その場合の定常流れを求め発生する圧力を調べる．簡単のため，壁面に入射した分子は乱反射するとした．壁面の温度は300 K，空気の初期温度および初期圧力は300 K，1 atmである．

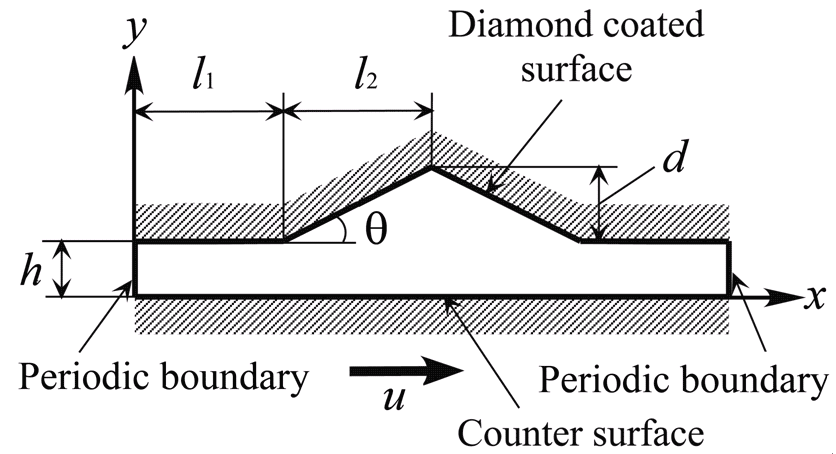
図4 計算領域

　図5に流速分布を示す．この結果はu = 10 m/s, l₁ = l₂ = 2.88 µm, d = 1.44 µm, h = 0.14µmの条件で得られた．下側壁面が右にu = 10 m/sで移動するため，図に示すような流れが誘起される．図6に凹部内の圧力，分子数密度，温度の分布を示す．温度が空間一様であるのに対し，分子数密度と圧力は相似の分布を示している．この結果および以下の結果はu = 10 m/s, l₁ = l₂ = 11.52 µm, d = 1.44 µm, h = 0.14µmの条件で得られたものである．凹部の左端の流入部で圧力は小さくなり，右側の流出部で圧力が高くなっている．揚力を得るためには圧力の変化が重要であるが，その変化は分子数密度の変化によって得られることがわかる．ここでは結果を示さないが，クヌッセン数が小さくなると，分子数密度および圧力の空間変化は小さくなり一様に近くなる．クヌッセン数が大きい場合にのみ，圧力変化が現れる．高クヌッセン数の場合には，分子の平均自由行程が流れの空間スケールに対して長いために衝突があまり起こらず，流路の狭くなるところに局所的に分子が集中することが許される．一方で低クヌッセン数の場合には，分子間衝突が頻繁に起こるために，分子の集中が阻害され，数密度分布が一様に近くなるのである．

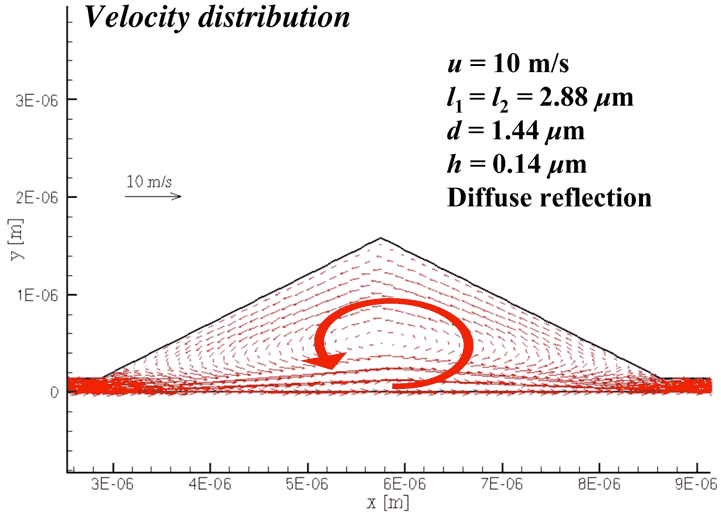
図5 流速分布

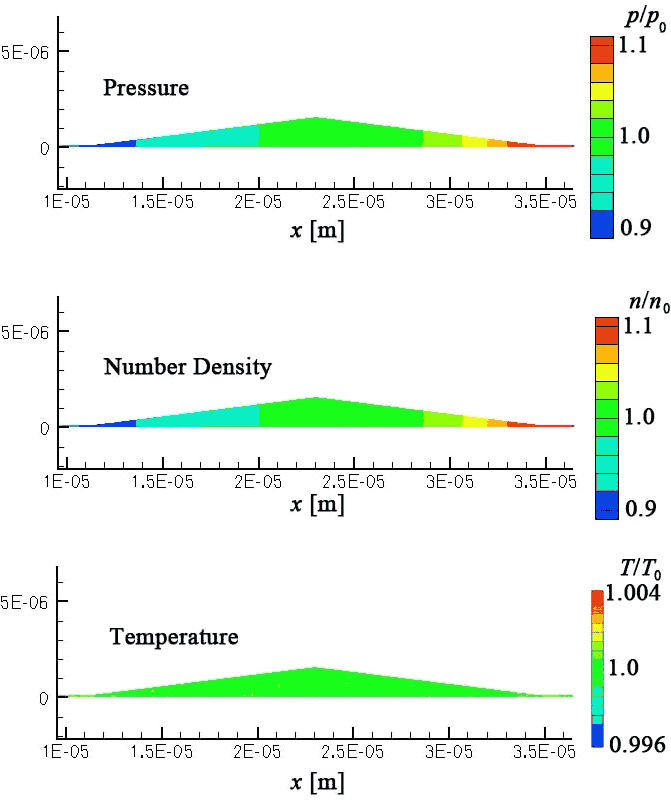
図6 圧力，分子数密度，温度の空間分布
(u = 10 m/s, l₁ = l₂ = 11.52 µm, d = 1.44 µm, h = 0.14µm)

　図7にスライダー表面にかかる圧力の分布を示す．図下部に黒い実線にて流路の形状を示している．流路形状はy方向（高さ方向）に拡大して表現されていることに注意されたい．スライダーの上面は1 atmの大気にさらされているため，下部表面の圧力が1 atmより大きい場合には上向きの力を，1 atmより小さい場合に下向きの力を得ることになる．この図の水色の楕円で囲まれた凹部の圧力分布に注目されたい．凹部の流入部で下向き，流出部で上向きの力がかかっている．分布形状の対称性から，上下の力が相殺することが分かる．次に緑色の楕円で囲まれた平坦部の圧力分布に注目されたい．平坦部では左の流入部で観察される上向きの力が放物線形状を描いてはじめ緩やかに，やがて急激に減少している．平坦部の右の流出部では流入部と同じ大きさで下向きの力がかかっている．この分布形状から平均して上向きの力が得られるのがわかる．ここでは2097 Paの平均ゲージ圧力を得た．一方，実験で用いられたスライダーの質量は280gで面積が1960mm²であるため，1400 Paのゲージ圧力でスライダーは浮上する．本計算で得られた圧力でスライダー浮上のメカニズムが説明できる．ここで取り扱った流れは流路のスケールが非常に小さいマイクロ気体流れ（高クヌッセン数流れ）であるが，流れのスケールが大きい非圧縮性の連続体として取り扱った場合，レイノルズ方程式の解から平行平板間の圧力分布は直線形状となる．図8にその場合の平坦部の圧力分布を緑色の実線で示している．圧力分布が直線形状になった場合にはその対称性から上下の力が相殺し，やはり揚力が発生しないことが分かる．

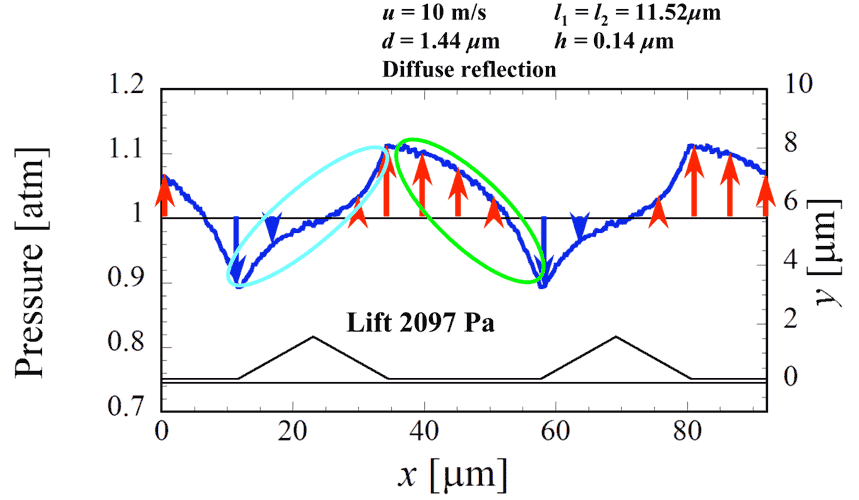
図7 スライダー表面の圧力分布

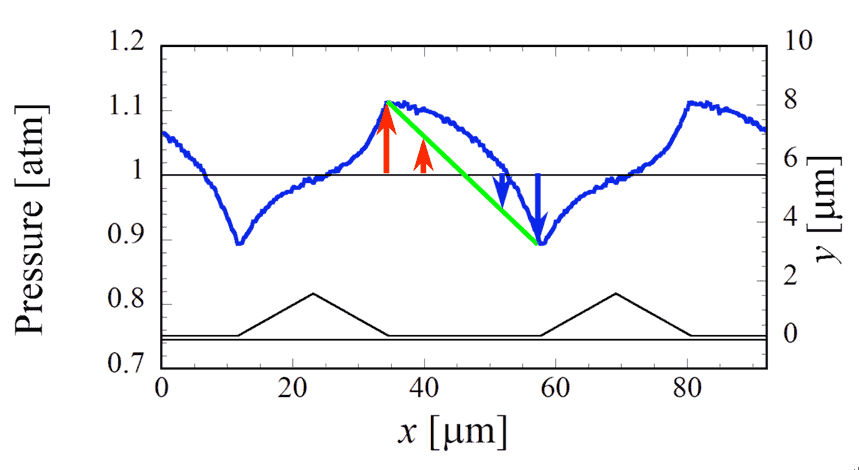
図8 スライダー表面の圧力分布（非圧縮の連続体流れの場合）

3. おわりに

　 本研究で得られた結果から，ダイヤモンド膜浮上のメカニズムが明らかになった．本研究で観察された圧力発生はマイクロ気体流れ（高クヌッセン数流れ）特有の現象であり，新しい気体潤滑機構を示している．

謝 辞

　 本研究は実験グループと数値シミュレーションのグループによる共同研究である．数値シミュレーショングループは，独立行政法人日本学術振興会 科学研究費補助金 基盤研究（C）(20560146)の助成をうけた．また実験グループは，独立行政法人日本学術振興会　科学研究費補助金 基盤研究（C）(19560132)の助成を受けた．本数値結果は東北大学流体科学研究所未来流体情報創造センターのスーパーコンピュータSX-8を用いて得られた．

文 献

(1)	A.Eldemir et al., Surf.Coat.Tech, 120-121 (1999) 565.
(2)	T.Takeno et al., Diam.Relat.Mater. 14 (2005) 2118.
(3)	I.Nakamori et al., Diamond Relat. Mater., 14 (2005) 2122.
(4)	T. Takagi and H. Miki, Non-lubrication Sliding Mechanism and Nano-Micro Ground Effect of a Fine Structure Diamond Surface,Nano-Mega Scale Flow Dynamics in Highly Coupled Systems, Chap. 2, (2007) pp.21-56
(5)	G. A. Bird, Molecular Gas Dynamics and the Direct Simulation of Gas Flows, Clarendon Press, Oxford, (1994).
(6)	K. Nanbu, Journal of the Physical Society of Japan, Vol. 49, (1980), pp. 2042-2049.
(7)	南部健一，ボルツマン方程式の確率解法（数値流体力学，保原　充・大宮司久明編，東京大学出版会，1992），pp. 287-324