流れ 2009年4月号 目次
― 特集テーマ: 流体工学により解明される自然界,そこから生まれる新技術 ―
| リンク一覧にもどる | |
トンボ型飛翔ロボットの研究開発
|
1.はじめに

図1 シオカラトンボのフリーフライト映像
(▲図をクリックすると動画を開始)
トンボは大変身近に見ることのできる昆虫であるが,トンボの飛行能力が如何に凄いものであるかということは,必ずしも認識されていない.トンボはホバリングから急旋回,高速飛行等の自在な飛行をいとも簡単に行っているように見えるが,航空工学の観点からみるとこれは凄いことなのである.図1に,ホバリングから右旋回を行うシオカラトンボの高速度ビデオの映像を示した.トンボは1秒間に30回ほど羽ばたいているが,高速度撮影することによって羽の動きがよく分かる.
ホバリングから右旋回に移るときに,前後左右のそれぞれの羽が微妙に異なった動きをしていることが見て取れる.このような各羽の異なった動きによって右旋回のための空気力(この場合,ヨーイング・モーメントやローリング・モーメント)を生成し,しかも同時に自重を支えるための揚力や前進飛行のための推進力も生成していることになる.トンボのようにホバリングから高速飛行まで自在な飛行を行う小型飛翔ロボット(MAV(Micro Aerial Vehicle))を開発することが出来れば,人が容易に近づけないような災害現場等に飛ばして,種々の探索活動に役立てることができるであろう.国内外でこのような飛翔ロボットの研究開発が活発に行われている1).筆者らは,トンボのように2対の羽根を持つトンボ型の飛翔ロボットの研究開発を進めている.本稿では,このようなロボット開発に必要な要素技術のうち,数値シミュレーション技術と共振型羽ばたき翼の開発状況について概要を報告する.
2.要素技術開発の現況
2.1 数値シミュレーション技術
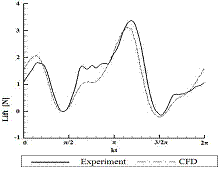
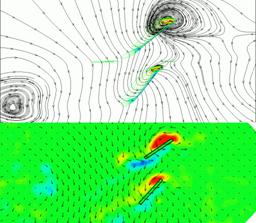
数値シミュレーション技術は,このようなロボット開発に不可欠な研究開発ツールである.すなわち,2対の羽をどのように羽ばたけばどのような空気力が生成されるか,あるいはその生成メカニズムはどのようになっているのかをあらかじめ知ることが出来なければ,このようなロボットの設計は基本的に不可能である.筆者らは,羽ばたき運動を行う2対の羽まわりの非定常粘性流れの数値シミュレーションが可能な3次元ナビエ・ストークス・コード(3D NSコード)を独自に開発した2)3).また,この3D NSコードの精度や信頼性を検証するために,想定したトンボ型ロボットの2対の羽根(矩形平板翼)のスケールモデルを搭載した非定常流体力計測装置を製作した.図2のビデオに示すように,回流式の水槽4)中において,種々の羽ばたき運動をパソコンからの指令とサーボモータによって行わせ,翼根に貼った歪ゲージによって,非定常流体力を計測することができる.また,3次元粒子画像流速測定装置(3D PIV装置)により,羽ばたき翼まわりの流速場の計測も行っている.実験を空中ではなく水中で行う理由は,非定常実験で問題となる翼の慣性力が流体力に比べ小さく,高精度の流体力計測が可能なためである.また,相似パラメータである無次元振動数とレイノルズ数は空中における実機と水中におけるスケールモデル(実機の2.5倍)でほぼ合わせることが可能である.図3に,ホバリング飛行条件下における1サイクル間の揚力(垂直方向の力)の時間変動について3D NSコードによる計算結果と実験値を比較している.実験と計算は極めてよく一致していることがわかる.図4は,羽ばたき条件は異なるが,同じ半載翼の揚力最大時における50%セミスパン位置での(翼断面まわりの)フローパターンを比較したものである.上図が3D NSコードによる流線と渦度の分布,下図が3次元PIV装置によって測定した速度ベクトル場と渦度の分布を示している.上の翼が前翼で下の翼が後翼で前後翼の前縁付近に生じた強いはく離渦による負圧によって大きな揚力が生じているものと思われる.また,3D NSコードと3D PIVの結果はよく一致していることがわかる.本3D NSコードは,弾性翼の空力弾性応答も取り扱える5)ために,次節で述べる共振型羽ばたき翼の開発でも威力を発揮している.

図2 回流式水槽と非定常流体力計測装置
(▲図をクリックすると動画を開始)
 |
 |
| 図3 非定常揚力変動の実験値と 数値シミュレーション結果の比較 |
図4 50%セミスパン位置における(翼断面まわりの) フローパターン (3D NSコードと3D PIVによる結果の比較) |
2.2 共振型羽ばたき翼の開発
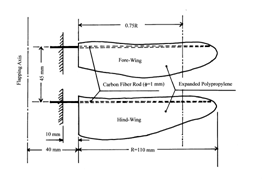
昆虫型飛翔ロボットでは,超軽量で効率良く推力や揚力を生成できる羽ばたき翼の開発が不可欠である.このような羽ばたき翼の一つの候補として筆者等はこれまでに弾性翼または弾性的に支持された翼の共振振動数付近で,小さなトルクで翼を加振して,大振幅の羽ばたき運動を実現する所謂「共振型羽ばたき翼」の研究開発を行ってきた.最初は剛体の翼をフラッピング(機軸周りの回転運動)とスパン方向の軸周りのフェザリング(ピッチング運動)の2自由度のそれぞれをバネで支持する「2自由度共振型羽ばたき翼」の研究6),7)を進めてきたが,現在はその発展型として翼自身が弾性体である「多自由度共振型羽ばたき翼」5)の開発に力を入れている.ここでは,後者を紹介する.図5に「多自由度共振型羽ばたき翼」の翼平面形とその構造を示す.
 |
 |
| 図5 多自由度共振型羽ばたき翼の 平面形状と構造 |
図6 静止推力の測定 (▲図をクリックすると動画を開始) |
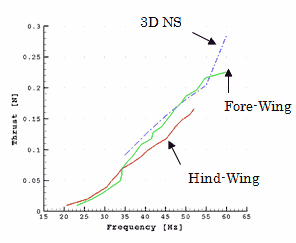
翼の平面形はオニヤンマの前後翼の平面形状と相似である.また,構造的には直径1mm のCFRP製のロッドにEPP(Expanded Polypropylene)の薄板(前翼の板厚が1.5mmで後翼が3mm)を貼り付けただけの簡単な構造をしており,一枚の翼の質量は前翼が0.25g,後翼が0.30gと超軽量である.これら前後翼それぞれ一枚の静止推力(静止空気中で翼を加振したときに生成される空気力で,ホバリング飛行条件における揚力に対応する)を計測している様子を図6のビデオに示す.この映像は,翼の根元を片振幅10度でフラッピング方向に60Hzで加振している場合を示す.また,推力生成に重要な翼のフェザリング(捩じり運動)を見るためにストロボの光を当てている.この場合のフェザリング運動は空力弾性(翼の弾性力と慣性力および空気力の相互作用)変形のみによって生じている点に注意すべきである.また,フェザリング運動のフラッピング運動に対する位相差が約90度付近になることが大きな推力を生成する上で重要である.このようにして計測された静止推力の振動数に対する変化を図7に示す.
 |
 |
| 図7 前翼および後翼の静止推力 | 図8 ホバリング実証模型 |
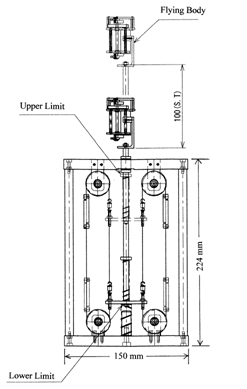
この図から例えば,羽ばたき振動数40Hzで翼一枚当り約10gfの推力が生成されていることが分かる.このことは,この羽を4枚搭載したトンボ型ロボットは約40Hzの羽ばたきによって,重量約40gfの機体をホバリング状態で持ち上げる能力のあることを意味する.このことを実証するために,図8に示すホバリング実証機を製作した.このホバリング実証機は,1個のコアレス・モータと2対の羽を翼根で振幅10度で加振するためのカムとギアー,機体全体の振動を抑えるためのカウンターウエート等で構成され総重量が35gfである.(パワーはリード線を通して外部より供給される.) この機体はまだ姿勢安定のための制御を行っていないので,図9に示すテストベッドの先端に取り付けられている.このテストベッドは,図8の飛翔体部分が自重以上の揚力を生成すると,飛翔体部分が上昇運動を起こすように設計されている.図10のビデオは,リード線を含む総重量約40gfの機体が上昇運動を行う様子を示す.図11には,本共振型羽ばたき翼の揚力最大時における68%セミスパン位置での前後翼断面まわりのフローパターン(流線と渦度)を示した.現在,前後左右それぞれの羽の羽ばたき運動を独立に制御して,安定なフリーフライトを行うモデルの設計・製作を進めているところである.
 |
|
| 図9 ホバリング実証のためのテストベッド | 図10 ホバリング実証試験映像 |
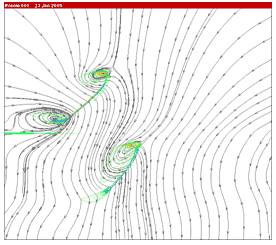
図11 共振型羽ばたき翼まわりの流れの様子
(3D NS コードによる流線図と渦度)
3.おわりに
日本文理大学では,文部科学省の「ハイテク・リサーチ・センター整備事業」の助成金を得て「昆虫型超小型飛翔ロボットの研究開発」というプロジェクトを進めている.本稿では「共振型羽ばたき翼を搭載したトンボ型飛翔ロボット」に関連した開発の現況を報告したが,この他昆虫の優れた滑空特性に着目して開発したコルゲート翼(凹凸翼)を装着した「非羽ばたき方式の小型飛翔ロボット」(固定翼プロペラ駆動)の研究開発や「昆虫の羽ばたき翼による非定常空気力生成メカニズムに関する研究」8),トンボのフリーフライトを高速度ビデオで撮影してその映像を定量化することにより「トンボの種々のマヌーバ時の翼運動と機体運動の関係を解明する研究」9)等も行っていることを付記する.また,本稿を作成するに当たり,本学の河邊博康教授,永井弘人助教,上澤裕一研究員の協力を得た.
文献



