流れ 2009年4月号 目次
― 特集テーマ: 流体工学により解明される自然界,そこから生まれる新技術 ―
| リンク一覧にもどる | |
数値流体解析による長大橋梁の空力と振動の予測
|
1. まえがき
旧タコマ橋の落橋から分かるように,長大橋の設計においては橋桁の耐風安定性を定量的に評価することが極めて重要である.現在,風による橋の動的応答の重要性が広く認識され,風洞実験に基づく長大橋の耐風設計手法もほぼ確立されている.長大橋の耐風設計の詳細については「本州四国連絡橋耐風設計基準」1)や「橋梁の耐風設計,基準と最近の進歩」2)などから知ることができる.
橋梁の耐風設計は,設計風速の設定3),橋梁断面の空気力学特性の評価,橋全体の風による振動予測,各種のクライテリアの照査と様々なプロセスを経て実施されるが,中でも橋断面の空気力学特性の予測は,橋に作用する風荷重の評価やフラッター発振風速の照査に欠かせない重要な項目の一つであり,その予測精度は橋全体の耐風安全性評価に大きな影響を与える.本稿では,実橋梁断面の空力特性予測の現状を紹介すると共に,数値解析による長大橋の耐風設計の可能性を展望する.
2.橋梁の耐風設計
橋桁は流れに対して「鈍い」物体であり,風により様々な空力振動が発生する.橋の耐風性能を評価するには橋桁の空力特性を予め知る必要がある.
例えば,風の乱れにより発生する不規則な振動については,橋桁の定常空気力係数が分かれば,準定常理論に基づき,橋のガスト応答を求めることができ4),また定常空力係数の勾配などからギャロッピング発振風速を推定できる5). 更に,橋桁の耐風安定性を照査するには,橋桁の非定常空気力係数を用いて複素固有値解析によりフラッター発振風速を求めることが可能である6).一方,橋桁の固有振動と後流渦の周波数が一致して起きる渦励振の問題では,流体と構造物の相互作用が重要であり,橋の振動振幅は流体と構造物の連成解析により直接求める必要がある.
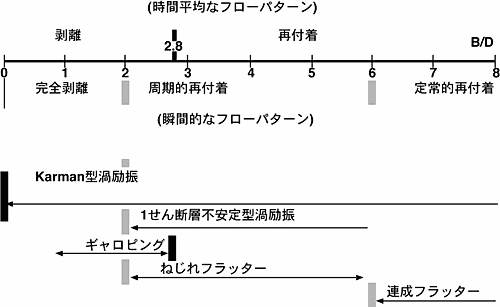
図1 流れのパターンと発生する空力振動との関係
図1には矩形断面に発生する空力振動の種別と矩形断面の辺長比(B/D)との関係を示す7).空力振動の種別は静止状態において断面まわりに形成されるフローパターン(完全剥離型,周期的再付着型,定常的再付着型)に基づき分類することができる.Karman型の渦励振は全ての断面において発生しうるが,ギャロピングは完全剥離型断面のみ発生し,1せん断層不安定型やねじれフラッターは周期的再付着型断面において発生する.また連成フラッターは定常的再付着型断面に関係する.橋の耐風設計を行う際には橋桁の辺長比からどのような空力不安定振動が生じうるかを大まかに知ることができる.
表1 空力振動評価に必要な空気力係数と評価手法
| 空気力と手法 評価項目 | 空気力係数 |
評価手法 |
ガスト応答 |
定常 |
2段階 |
ギャロッピング発振風速 |
定常 |
2段階 |
フラッター発振風速 |
非定常 |
2段階 |
渦励振の振動振幅 |
- |
連成解析 |
表1には橋の空力振動評価に必要な空気力係数と評価手法を示す.この表から分かるように,ガスト応答解析やフラッター解析では空気力係数を求めるステップと,その結果を用いて応答解析や複素固有値解析を行うステップに分けることができる.それに対して,渦励振の予測では,橋の振動振幅が空気力に影響を与えるために空気力と振動振幅の算定を同時に行う必要がある.橋の空力振動評価には以下に示す2つの方法が考えられる.
第1の方法は風洞実験による方法である.定常空気力係数については静的三分力計により測定する.一方,非定常空気力係数については強制振動法が用いられる.強制振動法はその名の示すとおり,強制的に正弦波的な振動を与えた模型に作用する変動風力を計測するもので,ロードセルを用いて慣性力をキャンセルしながら測定することにより求める.非定常空気力係数は得られた変動空気力の時系列波形にフーリエ変換を施すことで容易に求めることができる.更に,渦励振の振幅は自由振動法により求めることができる.この手法ではばね支持された模型を風の中で自由に振動させ,風速と応答の関係を直接求めることにより,橋桁の振動振幅を予測する.風洞実験は流体力学の相似則に基づいているため,空気力を正しく計測できれば,風洞実験から得られた空気力係数や橋の振動振幅は信頼性が高い.一方,上述したように強制振動試験では強制振動を与えるための特別な駆動装置が必要であり,設計者自身が空気力係数を求めることが容易ではない.
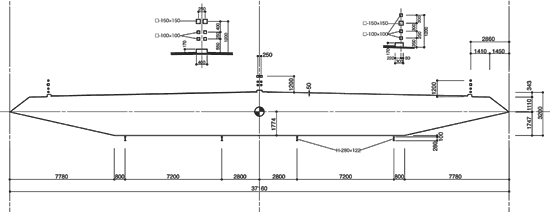
図2 主桁の断面図
近年,コンピュータ及び流体計算技術の進歩に伴い,数値解析により橋の空力振動を評価する第2の方法が提案されている.この方法では風洞実験とほぼ同じ手順を踏むが,風や模型を数値的に再現することから数値風洞と呼ばれている.例えば,定常空気力係数を求める場合には,まず橋桁表面の各計算格子における圧力を算出し,それらを表面全体にわたって積分することにより橋桁の平均空気力係数を求める.一方,非定常空気力係数を求める場合には,風洞実験と同じように,強制的に橋桁を含む解析領域を正弦波的に振動させ,橋桁に作用する変動風力を算出する.変動風力は表面圧力を積分することにより求めるため,風洞実験のように慣性力をキャンセルしながら測定する必要がない.更に,渦励振を求める際には流体と構造の連成解析を実施し,橋桁の振動と橋桁周りの流れ場との相互作用を予測しながら,振動振幅を求める.数値解析による空力振動予測では橋桁の形状,ばね常数,減衰定数を自由に変化させることができ,各種制御装置の効果も簡単に評価することができる.
以下,著者が最近数値解析により実橋梁断面における空力性能を予測した例を紹介し,数値解析による空気力係数の予測精度と実用可能性を明らかにする.
3.橋梁断面の空力性能の数値予測
橋桁まわりの気流は流体力学の基礎方程式であるナビエ・ストークス方程式(NS方程式)により記述される8).現在,橋梁断面の空力性能を数値的に予測する時にはレイノルズ平均型モデルと空間平均型LES(Large Eddy Simulation)モデルが用いられている.LESモデルを用いる場合,3次元解析が必要となり,計算時間はレイノルズ平均型モデルの場合に比べ長いが,平均空気力係数のみならず,変動空気力係数やパワースペクトル密度の迎角による変化を精度よく再現できることから,汎用性が高い手法と言える9).以下,数値解析による定常・非定常空気力係数,フラッター発振風速を紹介する.また実橋梁の渦励振による振動振幅の予測や空力制振装置の設置による振動振幅低減効果の予測については参考文献13を参照されたい.
3.1橋梁断面の定常空気力係数の解析例
まず斜張橋主桁断面の定常空気力係数の予測例を紹介する10).この例では静的三分力実験を模擬した解析を行い,主桁断面の定常空気力係数を算出すると共に,高欄などの付加物の影響を明確にする.また数値解析の予測精度を調べるために,縮尺1/60模型を用いた風洞実験を実施し,比較検討も行った.
図2には斜張橋主桁の断面図を示す.主桁の高さDは3.2m,幅Bは37.2m,辺長比(B/D)は11.6である.箱桁は流線型となっており,手すり,中央高欄,検査車レールも配置されている.

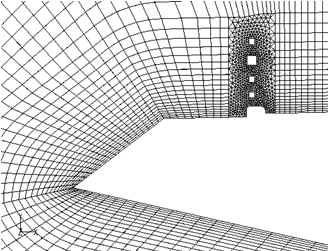
図3 主桁まわりの計算格子
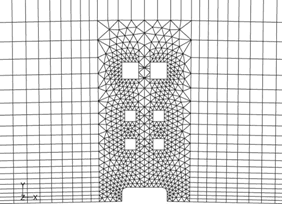
(a) 風上端部の手すり
 |
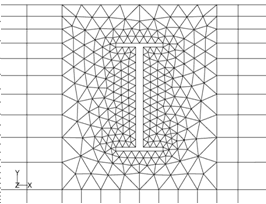 |
| (b)中央高欄 | (c)検査車レール |
図4 手すり,高欄,検査車レールまわりの計算格子
図3には再現された主桁断面及びそのまわりの計算格子を示す.主桁上面にある手すり,中央高欄及び主桁下面の検査車レールを忠実に再現したが,手すりと高欄の鉛直支柱の再現を省略した.全体の解析領域はx方向に105D,y方向に60D,スパン方向に3Dとした.主桁断面の中心は流入部から45Dの位置に設置した.図4には手すり,中央高欄,検査車レール近傍の計算格子を示す.
図5に平均抗力係数の迎角による変化を示す.図中のプロットはそれぞれ付加物がある場合とない場合の解析結果を示した.迎角α=0°付近では付加物がない場合の抗力係数は0.35であるのに対し,付加物がある場合にはその約3倍大きくなっている.同様な傾向は迎角10°まで続く.抗力係数の解析結果は風洞実験(実線)と同じ傾向を示した.
ただし,付加物がある場合の数値解析結果は実験値に比較してやや小さめになっている.そこで格子分解能の影響を調べるために,手すり,高欄,検査車レールまわりの格子数を増やして再度計算を行った.その結果を+印で図中に示す.抗力係数の予測誤差は約半分に減少した.更に格子数を増やしたが,抗力変化が見られなくなった.数値解析により求められた抗力係数が風洞実験の結果よりやや小さめになっている理由は,風洞実験模型にある手すりと高欄の鉛直支柱を数値解析で省略したことによるものと考えられる.
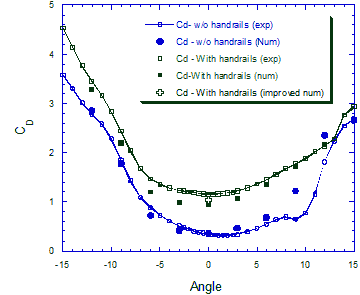
図5 抗力係数の迎角変化
図6にピッチングモーメント係数の解析結果を示す.風洞実験の結果とよく一致している.抗力係数と異なり,ピッチングモーメント係数は迎角α=0°付近で付加物の影響が殆ど見られず,迎角12度付近では大きな差が見られた.同様な傾向は揚力係数にも見られる.
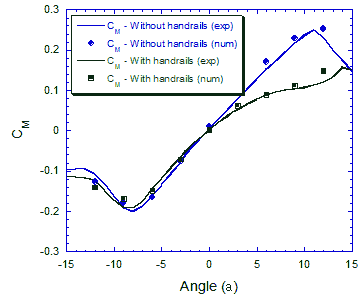
図6 ピッチングモーメント係数の迎角変化
ピッチングモーメント係数が迎角12度付近で大きな差が見られた理由を明らかにするため,橋桁まわりの流れのパターンを調べた.図7には主桁まわりの平均流線を示す.この図から,付加物がある場合には主桁先端で離れた流れが風上端部の手すりにあたることにより,主桁上面の剥離領域が大きくなっていることが分かる.この付加物がある場合とない場合の剥離領域の違いによって,主桁上面の圧力分布に大きな差が発生し,結果的にはピッチングモーメント係数に大きな差を生じさせた.
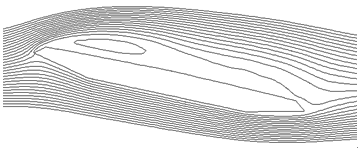
(a) 付加物なし
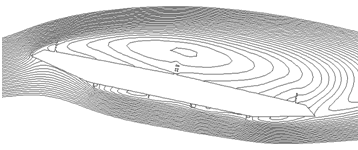
(b) 付加物あり
図7 主桁まわりの平均流線
以上の結果から,数値解析により実橋梁断面の空気力係数を求める場合,付加物の考慮が不可欠であり,また空気力係数を求める際には付加物付近の格子を十分に配置するように注意する必要がある.また実際の橋梁設計において重要である迎角0°付近では,付加物が抗力係数に大きな影響を与えるが,揚力係数およびピッチングモーメント係数に与える影響は小さい.この結果からは付加物の存在が主桁のガスト応答に大きな影響を与えると予想される.
3.2 強制振動による非定常空気力の解析例
次に数値解析による実橋梁断面の非定常空気力を求めた例を示す10),12).扁平断面ではギャロピングは生じなくなる反面,鉛直たわみとねじれの振動に伴う揚力およびピッチングモーメントとの位相差に起因する発散型の不安定振動,すなわち,連成フラッターを生じる可能性があり,耐風設計においてはフラッター発振風速を照査する必要がある.本節では,まず強制振動法を模擬した解析を行い,鉛直とねじれの一自由度の強制加振解析から非定常空気力係数を算出し,フラッター解析の入力データとした.そして既往の矩形断面の風洞実験と比較し,数値予測の精度検証を行った.
非定常空気力の解析は辺長比10と20の矩形断面及び3.1節で示した実橋梁断面(付加物がある場合とない場合)について行った.図8には解析格子を示し,中央部分の計算格子をねじることによりねじれ加振を模擬し,また点線で囲まれている計算格子を上下に動かすことにより鉛直加振を模擬した.なお,主桁及び付加物まわりの計算格子は図3と図4に示すとおりである.
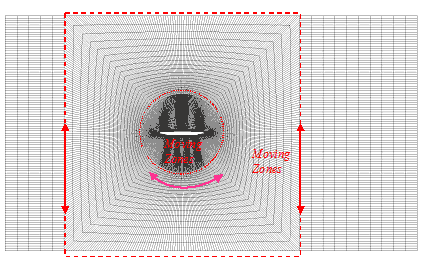
図8 移動格子によるねじれと鉛直加振解析
加振振幅は松本ら11)による実験を参考に,鉛直加振についてはB/40,ねじれ加振については2°とした.解析は無次元時間にして約700~800まで行い,非定常空気力係数はその内,解析の始めの過渡部分を除き,変動が安定になった無次元時間約500の部分について,得られた時系列のフーリエ展開を行うことでその加振振動数成分から同定した.非定常空気力係数は松本ら11)の表記法に従い,次式により定義する.
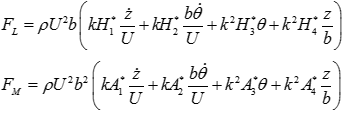
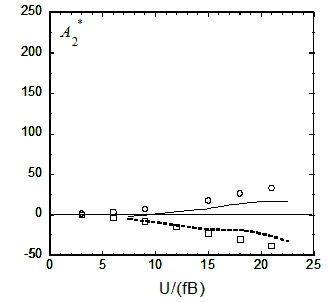
図9 非定常空気力係数の比較
図9には揚力およびピッチングモーメントの時系列から求めた辺長比10と20の矩形断面における非定常空気力係数A2*の結果を示し,図中の実線(B/D=10)と点線(B/D=20)は風洞実験の結果を示す.いずれのケースにおいても,数値解析の結果は風洞実験とよい一致を示し,非定常空気力係数A2*はいずれの無次元風速においても負の値を示した.また実橋梁断面における非定常空気力係数はB/D=20の矩形断面に近い値を示した.
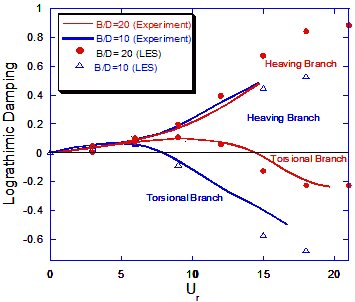
図10 矩形断面のフラッター解析結果の比較
図10には辺長比10と20の矩形断面のフラッター解析結果を示す.いずれの断面についても本解析結果は実験値とよい対応を示す.対数減衰率に関しては本解析結果が風洞実験と同様にたわみ分枝では常に正になっている.一方,ねじれ分枝では負減衰が発生し,またフラッター発振風速は辺長比が大きくなるにつれて高くなる.この傾向は解析結果が風洞実験と同様であり,本解析手法の有効性が示された.矩形断面のフラッター特性は前縁で剥離した流れの再付着に関係し,2次元解析で再現しにくいと言われている.同様な解析は実橋梁断面についても実施した.その結果,振動数及び対数減衰率とも辺長比20の矩形断面に近い値を示した.本橋梁断面は付加物があるものの,断面全体は流線型になっており,大きな剥離が抑さえられ,定常的な再付着型断面と同様な性質を示すものと考えられる.
以上の結果から,数値解析により予測された非定常空気力係数は,矩形断面に関する既往の風洞実験結果と一致し,また複素固有値解析から求められた振動数と対数減衰率とも実験結果とよく一致した.本橋梁断面の辺長比はB/Dは11.6 であるにも関わらず,非定常空気力係数はB/D=20の矩形断面に近い性質を示し,橋梁断面の流線型化は橋梁の耐風安定性の向上に貢献することがわかった.
4. あとがき
本報では数値解析による橋梁の耐風設計の現状を示し,実橋梁断面における空力性能の数値予測の可能性について著者が最近行った研究を例にして紹介した.解析例から分かるように,LESモデルを用いた数値解析により高欄や検査車レールなどの付加物を有する実橋梁断面における様々な空力現象を解明でき,定常・非定常空気力係数10),フラッター発振風速12),渦励振の振動振幅13)を精度よく予測することができる.現在,LESモデルを用いた3次元非定常解析は解析時間の面において構造解析のように気楽にできるとは言えないが,並列コンピュータを用いたケースパラレルと呼ばれる並列解析を実施すれば,風洞実験とほぼ同等の時間とコストで,実橋梁断面の空力特性を評価することが可能である.
実橋梁断面の空力性能予測を行う際には計算時間の他,計算格子の生成,解析条件の設定,ポスト処理などが設計者にとって負担になる.最近Web技術を利用してネットワーク上にブラフボディーの空気力特性を求める試みがなされている14).このシステムではユーザがインターネットを利用してWeb ブラウザからサーバにアクセスし,解析条件を入力するだけで空気力特性の予測が自動的に行われ,ポスト処理された計算結果や図面が自動にユーザに送られる.解析システムはサーバ・クライアント方式のため,ユーザのパソコン(クライアント)ではWebブラウザとメールさえ使えれば,どこからでも解析システム(サーバ)にアクセスでき,設計者が気楽に空力振動解析を行うことが可能になりつつある.
数値解析によるブラフボディーの空気力特性の予測技術は橋梁工学のみならず,同様な空力振動問題を抱える架空送電線,鉄道車両,風力発電設備の耐風安全性の向上にも貢献することであろう.
参考文献


