流れ　2009年9月号　目次

―　特集テーマ： 特集テーマ： 界面を含む流れのシミュレーション　― 分子シミュレーションで見た微小気泡 　 松本 充弘（京都大学） Cahn-Hilliard方程式を用いた界面追跡法による混相流のシミュレーション 　 辻本 公一（三重大学） 二相系格子ボルツマン法による混相流シミュレーション 　 稲室 隆二（京都大学） 界面体積追跡法の最近の進展とサブクール沸騰解析への展開 　 功刀 資彰，伊藤 啓，小瀬 裕男（京都大学） 気泡力学へのGhost Fluid法の適用 　 高比良 裕之，小林 一道（大阪府立大学） 編集後記 　 瀬田 剛（富山大学），岡森 克高（ソフトウェア クレイドル），細川 茂雄（神戸大学） 　｜　リンク一覧にもどる　｜

 

Cahn-Hilliard方程式を用いた界面追跡法による混相流のシミュレーション

辻本公一 三重大学

１．はじめに

　気液二相流は機械工学，原子力工学, 化学工学等の多岐にわたる分野において幅広く利用されている流れである．これに関連する様々な工業装置の性能向上には流動現象の詳細な知見が必要である.しかし，気液二相流は非定常な界面変形を伴う複雑な流動現象であるため，実験，理論のいずれにおいてもその現象を詳細に捉えることには限界があり，シミュレーションによる解析が有力な手段となる.界面を正確に追跡する数値解析法としてこれまで，CIP法,VOF法，MARS法, Front Tracking法，Level Set法等が開発されている．最近、筆者らはそれらと全く概念の異なる拡散界面モデル（Diffuse-Interface Model，DIM）を用いた二相流のシミュレーションについて研究を進めている．このDIMは計算手順が簡便であるが，応用例は多くはなく数値精度や実行上の問題点など性能が十分に明らかにされていない. ここでは未完のものも多いが、気液二相流れへのDIMの適用を検討した結果を紹介させていただく.

　 なお,DIMについては,高田による本ニュースレター（2008年4月号 高田尚樹，自由エネルギー拡散界面モデルの二相流数値解析への導入 ）⁽¹⁾の記事で優れた解説が行われており,本分野を理解する上で大変参考になる.

 

２．解析方法

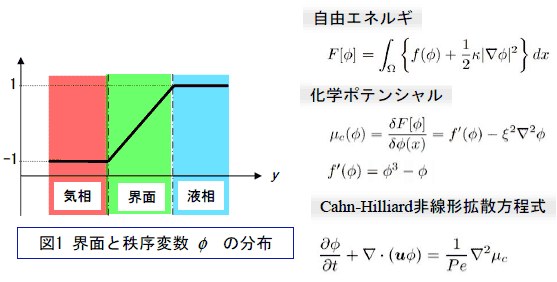
　有限な厚さを持つと想定される界面中で, 相が連続的に変化するとみなすと, 流体の質量密度または成分濃度に相当する秩序関数φに基づき,自由エネルギF[φ]が与えられる. 自由エネルギが最小化される平衡状態において二相が分離・共存することから, この自由エネルギを最小化する化学ポテンシャルが導出され,さらに化学ポテンシャルの勾配に比例した界面近傍での二相の拡散に関するCahn-Hilliard方程式(CH式)⁽²⁾が導出される. このCahn-Hilliard方程式に対流項を加え,ナビエストークス式を組み合わせたModel H^(3),(4)と呼ばれる方程式系を通常の有限差分法で離散化して解析が行われた.

 

３．解析結果

3.1　上昇する単一気泡のシミュレーション

　実験データと比較検証が可能な上昇する単一気泡のシミュレーションを行い，DIMの妥当性について検証した．

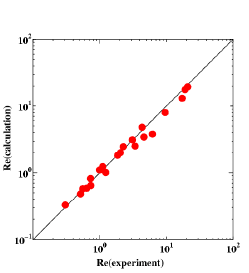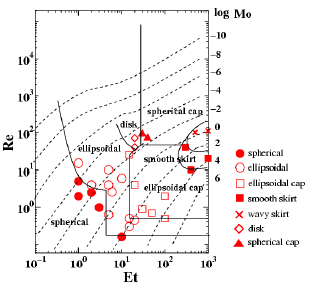
図２　　気泡特性図	図３　気泡レイノルズ数の比較

　図２はDIMを用いた２次元計算から得られた気泡特性図である．図の縦軸は気泡レイノルズ数，横軸はエトベス数，破線はモートン数を示している．図中の記号は計算結果の気泡形状を表しており実線は気泡形状を整理して引いた境界線である.形状の分布特性は実験結果と定性的に一致している．図３は実験と計算の気泡レイノルズ数の比較を示している．プロットされた点はすべて実線近傍に分布しており，実験とよく一致していることがわかる．また,この解析からCH方程式を解く際、陰的スキームの導入が保存性や収束性の改善に寄与することが明らかにされた⁽⁵⁾．

 

3.2　時間発展型の液膜噴流のシミュレーション

　液体の微粒化技術は, エンジン内の燃料噴霧, 噴霧塗装,噴霧乾燥, 粉末製造, 農薬散布などへ応用されている.これら技術の高度化には, 微粒化の詳細なメカニズムの解明に基づく流動制御が必要である. 最近, 液体噴流のDNS(Direct Numerical Simulation)が行われるようになり液体噴流の詳細な崩壊過程が再現されている. しかし, より詳細な二次的崩壊過程を追跡するには全てのスケールを含めた空間発展型よりは解像度不足を解消することができる時間発展型の方が有利と考え平面液膜噴流のシミュレーションを行った.　図４に座標系と計算領域を示す. 座標系はx 方向を主流方向, y 方向をスパン方向, z 方向を液膜厚さ方向とし,境界条件として各方向に周期条件を用いた. 計算領域は液膜厚さをz0 として, Hx×Hy×Hz = 6z0×6z0×6z0 の立方体領域とし, 格子数はNx×Ny×Nz = 128×64×120,レイノルズ数 Re = 4500, ウェーバー数 We = 26036 とした．

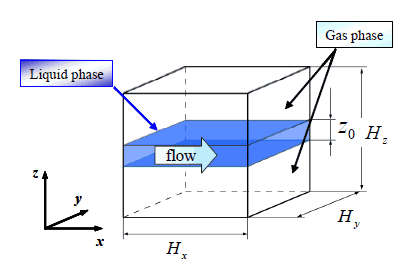
図４　計算領域と座標系（液膜噴流）

図５　界面分布

図６　渦構造（第二普遍量の可視化；液相（赤），気相（灰））

　図５は瞬時の液膜界面の可視化画像を左端から順に時間経過ごとに並べたものである. 時間とともに界面の揺らぎは大きくなり, 噴流中心付近まで乱れる.その後,界面の激しい乱れや液滴の発生が顕著になり,糸状の液体の突起であるligament の発生が確認できる. ligamentや液滴の生成はこれまでにも言及されている液体の微粒化の際に現れる特徴的な構造で，時間発展型のシミュレーションで液膜噴流の微粒化を追跡することが可能であることが分かる. 図６は速度勾配テンソルの第二不変量により渦構造を可視化したものである. 図中の灰色部は気相の，赤は液相での渦を表す. 界面の揺らぎが生じ始め,液相では界面近傍だけでなく液相の内部にも渦が見られる．気相の渦構造は界面近傍に加え界面から離れた位置にも存在している. DIMによりこのような3次元乱流場の詳細な解析が可能であることがわかった⁽⁶⁾．

 

3.3　IB法との組み合わせによる微小流路への樹脂注入のシミュレーション

　射出成型に関連するシミュレーションを考えた場合，考慮しなければならない要素として，非定常流れであること，粘弾性効果を示す樹脂特性について精度よく表現する構成方程式を導入すること，高温状態にある溶解された樹脂と金型間の熱移動を連成させて解析すること等が上げられる．これらは単相流の解析条件で，これまでは周囲流体（空気）との干渉は比較的無視されてきた．特に効率化による射出速度の高速化の要求もあり，周囲流体との干渉による樹脂挙動の不安定化は無視できず，精度よい解析手法の確立が求められている．そこでDIMと金型のような複雑な流路形状に簡便に対応する方法としてIB 法（Immersed Boundary Method）を採用した解析手法の検討を行った⁽⁷⁾．

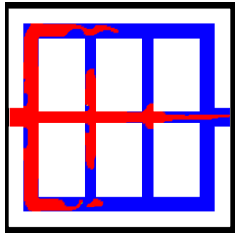図７　任意形状（円形）の流路への樹脂の注入（赤：樹脂,青：空気）	図8　微小流路への樹脂の注入（赤：樹脂,青：空気）

　図７は下から樹脂が流入し，任意物体（円形領域）を通り過ぎる流れを解析したものである．任意形状に樹脂が浸透することなく正しく解析されていることがわかる．図8は微小流路内に樹脂が充填されていく過程をシミュレーションしたものである．微小流路をつくるためにIB法を用いて流れ場に複数個の物体を配置した．入り口部の樹脂によるレイノルズ数はRe = 1.92である．微細流路のため絶対的なレイノルズ数は極めて小さいにもかかわらず，図から樹脂が蛇行し充填される様子から,気相の不安定な流れに呼応して樹脂にも不安定な流れが誘起されていることがわかる．このことからも二相流の解析は必要で,IB法とDIMを組み合わせた解析スキームが有効な手段となることがわかる．

 

3.4　相変化のシミュレーション（プール沸騰）

　沸騰，凝縮などの相変化を伴う流れは工業的に多くの分野で扱われておりシミュレーションでの解析が望まれている. しかし密度比が大きくなると相変化に伴う強い湧き出しが原因で、安定的に解析することは困難である．この課題も含め本研究では先に示したCH式に相変化モデルを導入した計算スキームを提案している⁽⁸⁾⁽⁹⁾．

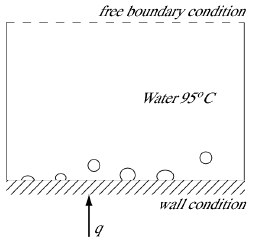
図９　計算条件（プール沸騰）	図10　瞬時の沸騰の可視化結果（白色部；蒸気,　薄青色部；水）

　図９は計算条件を示している．水平方向境界面を周期条件，下境界面を壁面条件，上境界面を自由流出条件とする．気液の物性値として密度比 ρg /ρｌ=0.001,初期条件として計算領域内の温度T=95℃，飽和温度をTsat=100℃とした.下壁面の温度Twallを一定とし,加熱度ΔT=Twall-Tsat=30[K]の場合について計算した．図10は最近行った3次元計算の可視化結果である．ここには図示しないが沸騰の様子を追跡すると,壁面において加熱され飽和温度を超えた水は相変化し,壁面上に蒸気膜を形成する．その後発生した蒸気膜は不安定になり浮力と表面張力により気泡となる．気泡となった蒸気は浮力によって壁面から離脱,上昇し,気泡のなくなった地点で再び蒸気が発生する．このような比較的密度比の大きい3次元シミュレーションにはCH式の陰的スキームの改良が重要な役割を果した^（9）．実験結果と沸騰現象の定量的な一致には壁近傍のモデリングがさらに必要となるが,比較的密度比の大きい相変化を扱える基本スキームが完成された.

 

４．おわりに

　DIMによる様々な気液二相流れの計算に挑戦し,そのたびごとにCH方程式の解法を改良することに精力を傾けてきた．この課題については,まだ充分な解決はされていないが既存の提案されるスキームを参考に,多様な用途に向けた安定なDIMに対する数値スキームの完成を目指している.

 

謝　辞

　本稿執筆に関するデータ作成は，三重大学大学院工学研究科 機械工学専攻 流動現象学研究室の学生ならびに卒業生の多大な協力によるものです.ここに記して謝意を表す．

 

参考文献

(1)	Takada, N., （http://www.jsme-fed.org/newsletters/2008_4/no4.html#ctop）
(2)	Cahn, J. W. and Hilliard, J. E., J. Chem. Phys., Vol. 28 (1958), pp. 258-267.
(3)	Hohenberg, P.C. and Halperin, B.I., Rev. Mod. Phys, Vol. 49 (1977), pp. 435-479.
(4)	Lowengrub, J. and Truskinovsky, L., Proc. R. Soc. Lond. A Vol. 454 (1998), pp. 2617-2654.
(5)	Maesoba, Y., Tsujimoto, K., Mizutani, Y., Shakouchi, T. and Ando, T., Proceedings of the 19th Computational Fluid Dynamics Conference,CD-ROM (2005-12), CD-ROM, Paper No. B5-3.
(6)	Tsujimoto, K., Wada, T., Nagawoka, M., Shakouchi, T. and Ando, T., Proceedings of the 22th Computational Fluid Dynamics Conference, CD-ROM (2008-12), CD-ROM, Paper No. C3-2.
(7)	Tsujimoto, K., Daimon, N., Shakouchi, T. and Ando, T., Proceedings of the 21th Computational Fluid Dynamics Conference,CD-ROM (2007-12), CD-ROM, Paper No. C3-5.
(8)	Tsujimoto, K., Mizutani, Y., Shakouchi, T. and Ando, T., Proceedings of the 20th Computational Fluid Dynamics Conference,CD-ROM (2006-12), CD-ROM, Paper No. F7-4.
(9)	Tsujimoto, K., Kambayashi, Y., Shakouchi, T. and Ando, T., 6th Int. Sym.Turbulence, Heat and Mass Transfer, 2009, CD-ROM.