流れ　2009年9月号　目次

―　特集テーマ： 特集テーマ： 界面を含む流れのシミュレーション　― 分子シミュレーションで見た微小気泡 　 松本 充弘（京都大学） Cahn-Hilliard方程式を用いた界面追跡法による混相流のシミュレーション 　 辻本 公一（三重大学） 二相系格子ボルツマン法による混相流シミュレーション 　 稲室 隆二（京都大学） 界面体積追跡法の最近の進展とサブクール沸騰解析への展開 　 功刀 資彰，伊藤 啓，小瀬 裕男（京都大学） 気泡力学へのGhost Fluid法の適用 　 高比良 裕之，小林 一道（大阪府立大学） 編集後記 　 瀬田 剛（富山大学），岡森 克高（ソフトウェア クレイドル），細川 茂雄（神戸大学） 　｜　リンク一覧にもどる　｜

 

気泡力学へのGhost Fluid法の適用

大阪府立大学　高比良裕之，小林一道

1.　はじめに

　界面を含む流れをEuler的に解析する際，界面または衝撃波における接触不連続面での大きな打ち切り誤差が問題となる．一般的なEuler的手法による数値計算では，界面での物理量の不連続に起因する分散誤差を取り除くことに重点を置いていたため，散逸誤差の影響が容認されていた．Ghost Fluid法⁽¹⁾では，Level Set関数等で界面を捕獲し二流体を区別した上で，界面での境界条件を考慮して，別の流体の領域に仮想流体(Ghost Fluid)を定義することにより，界面を有する二流体の運動を，全領域に定義された二種類の単相流の支配方程式から決定する．この方法には，散逸誤差の影響が排除され，界面での不連続を鋭く捉えられるという利点がある．しかし，気液二相流のように一方の流体が他方に比べて非常に硬い流体の場合，界面での数値振動が起こりやすいなどの問題がある．本稿では，入射衝撃波と気泡との干渉問題を取り上げて，気泡崩壊問題へのGhost Fluid法の適用について概説する．

 

2.　Ghost Fluid法

2.1 概念

　Ghost Fluid法⁽¹⁾では，界面での境界条件を陽的に当てはめる代わりに，Ghost Fluidと呼ばれる仮想的な流体を定義し，陰的に界面での境界条件を捕らえる．その結果，界面の両側で不連続な分布となる物理量による誤差を解消する．界面の捕獲には，Level Set関数⁽²⁾を用いる．Level Set関数φは，界面から測った符号付きの距離関数であり，φ=0の集合が界面を表し，φ<0の領域が一方の流体を，φ>0の領域がもう一方の流体を表す．それぞれの流体は別のEuler方程式と状態方程式を満たしている．Level Set関数は，以下に示すLevel Set方程式により，時間発展される．

ここで，t は時間，u は流体の速度ベクトルである．いったん，Level Set関数の値が決まると，二種類の流体によって二つに分けられた計算領域が定義される．各々の格子点には，それぞれの流体についての各物理量(質量，運動量，エネルギー)が定義されているが，同時に，別の流体の領域に，一方の流体に対する仮想的な流体(Ghost Fluid)とその物理量を定義する．例えば， φ<0の領域に流体1，φ>0の領域に流体2が存在するものとすると，φ<0の領域にφ>0の領域の流体に相当する仮想的な流体(Ghost Fluid 2)を定義する．同様に，φ>0の領域にφ<0の領域の流体に相当する仮想的な流体(Ghost Fluid 1)を定義する．これにより，流体1とGhost Fluid 1を合わせて一つの流体が計算領域全体に定義され，同様に，流体2とGhost Fluid 2を合わせてもう一つの流体が計算領域全体に定義されたことになる．全計算領域で二種類の流体が定義されたことにより，それぞれの流体について独立に単相流の問題として支配方程式を解くことができ，各格子点で次の時間ステップでの二種類の物理量を求めることができる．一方，次の時間ステップでの界面位置を求めるためにLevel Set方程式を時間発展する．そして，次の時間ステップでのLevel Set関数の符号に基づき， φ<0の領域では流体1の物理量を採用して流体2の物理量を捨てる．同様に，φ>0の領域では流体2の物理量を採用し流体1の物理量を捨てる．これにより，次の時間ステップでの物理量が各格子点でただ一つに決定される．この手順を繰り返して任意の時間での各物理量を求める．

2.2 Ghost Fluidの定義

　 Ghost Fluid法は，二流体の問題を単相流の解法を用いて計算できることが大きな特徴であり，仮想流体の値の定義方法が重要となる．仮想流体は，境界条件を陰的に満たすように定義される．すなわち，法線速度，圧力のように界面をまたいで連続な物理量に関しては，実際の流体の値をそのままGhost Fluidの値として採用する．一方，接線速度やエンタルピーのように界面をまたいで不連続な物理量に関しては，界面を挟んだ一方の流体の物理量を法線方向に補間することによりGhost Fluidの値を定め，界面をまたいで物理量が連続になるようする．なお，多次元問題では，法線方向の補間にFast Marching Method ⁽³⁾を用いている．

　 圧縮性の気液二相流の数値解析では，気相と液相の音響インピーダンスが大きく異なるため，気液界面近傍で数値振動が非常に起こりやすい．そのため，Ghost Fluid法と合わせて，一次元のRiemann厳密解⁽⁴⁾を用いて気液界面近傍の物理量を補正し，数値振動を抑制する方法⁽⁵⁾が有効である．

2.3 界面捕獲の問題点

　 さて，式(1)の時間発展に伴い，Level Set関数φは流れにより歪められ，距離関数としての性質を失ってしまう．そのため，各時間ステップに，Level Set関数を再構築する必要がある．この処理は，「再初期化」と呼ばれるが，その際，数値誤差等により，界面位置が動いてしまい，質量保存性が悪くなるという問題がある．この問題の解決策には様々な方法が考案されているが，本稿では，Hybrid Particle Level Set法⁽⁶⁾を用いて，この問題に対処する．Hybrid Particle Level Set法では，界面近傍にLevel Set関数の正負に応じた符号の異なるマーカー粒子を配置し，それらを追跡することにより，界面が大きく変形する場合や，分裂，合体する場合にも精度よく界面を追跡できる特徴がある．

 

3.　ガラス壁近傍での水銀中の気泡と衝撃波との干渉問題

　上述のGhost Fluid法を用いた解析の一例として，ガラス壁近傍における水銀中の気泡と衝撃波との干渉問題^(7),(8)について概説する．さて，高出力の核破砕中性子源の開発において，大強度のパルス陽子ビームが水銀ターゲット中に入射すると，液体水銀内部では熱膨張により圧力波が生じ，この圧力波が液体水銀中を伝播する過程でキャビテーション気泡が発生する．キャビテーション気泡の崩壊は，容器壁面の損傷を引き起こし，容器の寿命低下の原因となる⁽⁹⁾．本数値計算の目的は，こうした壁面損傷の機構を解明することにある．本解析では，Futakawaら⁽⁹⁾の実験と関連して，気泡崩壊によるガラス壁面の損傷を扱った．

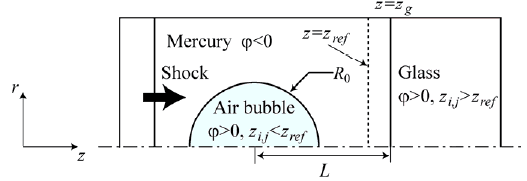
Fig. 1: Computational domain.

　図1に本計算のモデル図を示す．図1のように，最初，ガラス壁面から距離Lの位置に初期半径R₀の気泡が置かれている．気泡の左から伝播する入射衝撃波は，気泡と干渉の後，気泡の崩壊を引き起こす．本問題は空気，水銀，およびガラスの三相から成り，二種類の界面を有している．これら三相をStiffened Gas状態方程式⁽¹⁰⁾を用いてモデル化し，三相すべてに対して仮想流体を設定し，それらの運動をGhost Fluid法を用いて解析する．各相の支配方程式は軸対称二次元Euler方程式とする．なお，以下の計算では，衝撃波背後の圧力p_sを１GPa，その前方の圧力p₀を0.1013 MPaと設定した．本解析においては，三相の判別および二種類の界面の判別に注意が必要である．判別には，二種類のLevel Set法を用いるなど，いくつかの方法が考えられるが，ここでは，一つのLevel Set 関数を用いて判別した．すなわち，φ<0の値を持つ流体を水銀と定義し，φ>0の値を持つ流体を気泡内気体(空気)もしくはガラスと定義する．空気とガラスを区別するためには，ガラス壁の変形を考慮して，それぞれの流体の領域を決定しなければならない．いま，水銀－ガラス界面を挟んでLevel Set 関数の符号が変化することに着目すると，界面が格子点(k, j)と(k+1, j)の間にあるならば，φ_k,j×φ_k+1,j<0となる．すべてのr方向のj に対して，φ_k,j×φ_k+1,j<0となるkを探すことにより， (k, j)点のz座標z_k,jを求め，それをz_ref (j) = z_k,jと定義する．z_ref (j)を用いると，φ>0でかつz_i,j>z_ref (j)の領域にある流体がガラスと判別され，φ>0でかつz_i,j < z_ref(j)の領域にある流体が空気と判別される^(7),(8)．

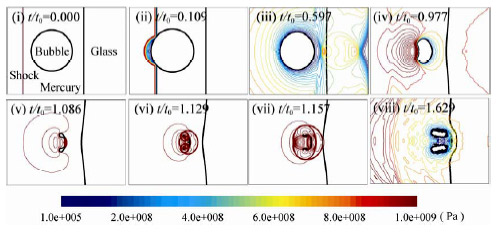
Fig. 2: Pressure contours for bubble collapse near a glass wall (L/R₀=1.56) ⁽⁸⁾.

　図2にガラス壁近傍における気泡崩壊時の圧力分布図の時間変化を示す⁽⁸⁾．気泡中心とガラス壁面との距離はL/R₀=1.56である．ここで図中のt/t₀は無次元時間を示しており， (は衝撃波背後の密度)である．図2 (ii)より，衝撃波が気泡に衝突すると，空気と水銀の音響インピーダンスの違いから，膨張波が水銀中に反射している様子がわかる．同様に，水銀とガラスの音響インピーダンスが異なるために，ガラス壁表面で，入射衝撃波の一部は透過し，残りは水銀中に反射する(図2(iii))．その後，気泡は上流側界面に液体ジェットを形成しながら収縮する(図2(iv))．このとき，気泡の収縮の際に生じる吸い込み流れにより，ガラス壁面は変形し気泡の方に引き寄せられる．そして，気泡界面に生じた液体ジェットは下流側気泡界面に衝突し，その際，衝突部から強い衝撃波が発生する(図2(v))．液体ジェットが貫通し，トロイダル状になった気泡は，最小体積に達した後再膨張する．気泡再膨張時に，トロイダル状の気泡から強い衝撃波が形成される．これら液体ジェット衝突時および気泡再膨張時に形成された二種類の衝撃波はガラス壁面に作用する(図2(vii))．図2(viii)より，衝撃波の高い圧力によりガラス界面はくぼみ，そのくぼみの中に気泡が進入していく様子が確認できる．このように，気泡崩壊時に形成される二種類の衝撃波が材料損傷の原因となる．

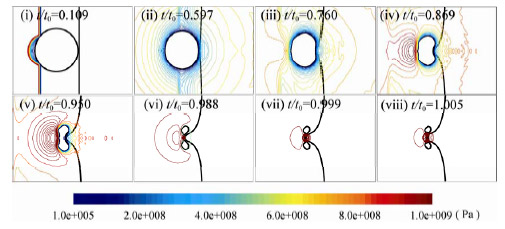
Fig. 3: Pressure contours for bubble collapse near a glass wall (L/R₀=1.06) ⁽⁸⁾.

　 図3は気泡中心とガラス壁面との距離がL/R₀=1.06の場合の計算結果である⁽⁸⁾．図2の場合と同様に，入射衝撃波との干渉により気泡は収縮するが，その際，気泡とガラス壁面との距離が近いときには，ガラス表面が気泡により引き寄せられることがわかる．その結果，気泡の並進運動は抑制され，上流側および下流側の両方の気泡表面から液体ジェットが形成され，気泡はリング状になる．このような気泡の挙動は，弾性壁近傍での気泡崩壊時に観測されるものであり，中立崩壊と呼ばれる^(11),(12)．

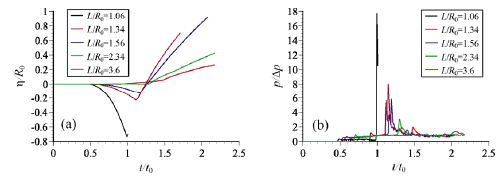
Fig. 4: Time histories of (a) displacement of the center of the glass surface and (b) pressure at the center of the glass surface ⁽⁸⁾.

　 図4に様々な気泡初期位置におけるガラス壁面の変位ηとガラス壁面中心での圧力の時間変化を示す⁽⁸⁾．なお，η<0の場合は，壁面はz 軸の負の方向に変位していることを示し，η>0場合はz 軸の正の方向に変位していることを示している．図4(a)より，初期気泡位置が壁面に近づくにつれて(L/R0が小さくなるにつれて)，壁面が気泡側に引き寄せられていることがわかる．また，図4(b)のL/R₀=1.34, 1.56のように，ガラス壁面圧力には，二つの圧力のピークが観測される．これらは，それぞれ，液体ジェットが下流側の気泡表面に衝突する際に形成される衝撃波ならびに気泡再膨張時の衝撃波を表している．こうした衝撃波が壁面に衝突するとガラス壁面は急速にz 軸の正の方向に変位する．その際，壁面に作用する衝撃圧力はL/R₀が小さくなるにつれ大きくなるため，壁面変形速度はL/R₀が小さくなるほど速くなる．

 

4.　おわりに

　本稿では，衝撃波と気泡との干渉問題を取り上げて，圧縮性気液二相流におけるGhost Fluid法について概説した．従来のGhost Fluid法に対して，気液界面近傍の物理量を，Riemann解を用いて補正することにより，非常に激しい気泡の崩壊に対して本手法が有効であることを示した．また，本手法を用いて，気体・液体・固体の三相の力学も扱える可能性が示された．本稿では，本手法を軸対称問題に対して適用したが，三次元問題への拡張も可能である ⁽¹³⁾．また，本手法は，生体組織と気泡との相互干渉問題等にも適用可能である⁽¹⁴⁾．本研究で用いたHybrid Particle Level Set法には，サブグリッド解像度の解析が行えるという利点があるが，より微細な界面構造を解析するには，微細格子が必要である．微細格子を用いた効率的な計算を行うために，本手法を拡張し，多重格子を用いたマルチグリッドGhost Fluid法の開発も行われている ⁽¹⁵⁾．本稿では界面での相変化を考慮せずに気泡の崩壊問題を扱ったが，気泡崩壊の極限物理を扱うには，相変化に起因する界面での熱・物質輸送現象が解明することが不可欠である．超高速で変形しながら体積変化する気泡の熱・物質輸送現象は，非常に困難な問題ではあるが，現在，マルチグリッドGhost Fluid法を用いてその解明に向けて研究に取り組んでいるところである．

 

参考文献

(1)	Fedkiw, R., Aslam, T., Merriman, B. and Osher, S., A Non-Oscillatory Eulerian Approach to Interfaces in Multimaterial Flows (the Ghost Fluid Method), Journal of Computational Physics, Vol. 152(1999), pp. 457-492.
(2)	Sussman, M., Smereka, P. and Osher, S., A Level Set Approach for Computing Solutions to Incompressible Two-Phase Flow, Journal of Computational Physics, Vol. 114(1994), pp. 146-159.
(3)	Adalsteinsson, D. and Sethian, J. A., The Fast Construction of Extension Velocities in Level Set Methods, Journal of Computational Physics, Vol. 148(1999), pp. 2-22.
(4)	Toro, E. F., Riemann Solvers and Numerical Methods for Fluid Dynamics, (1997), Springer-Verlag.
(5)	Takahira, H. and Yuasa, S., Investigation of Numerical Methods for Compressible Two-Phase Flows with the Ghost Fluid Method (2 nd Report, Improvement for Gas-Liquid Two-Phase Flow), Transactions of the Japan Society of Mechanical Engineers, Series B, Vol.72, No.723(2006), pp.55-63.
(6)	Enright, D., Fedkiw, R., Ferzeiger, J. and Mitchell, I., A Hybrid Particle Level Set Method for Improved Interface Capturing, Journal of Computational Physics, Vol. 183(2002), pp. 83-116.
(7)	Takahira, H., Matsuno, T. and Shuto, K., Numerical Investigations of Shock-Bubble Interactions in Mercury, Fluid Dynamics Research, Vol. 40 (2008), pp. 510-520.
(8)	Takahira, H., Kobayashi, K. and Matsuno, T., Direct Numerical Simulations of Interaction of Strong Shock Waves with Nonspherical Gas Bubbles near Glass Boundaries in Mercury, International Journal of Emerging Multidisciplinary Fluid Sciences, Vol.1 (2009), pp.85-99.
(9)	Futakawa, M. et al., Cavitation Erosion by Proton Beam Bombarding Mercury Target for Spallation Neutron Source -Damage Potential Evaluation by Measuring Acoustic Vibration-, Proceedings of the 6th International Symposium on Cavitation, (2006), Total 6 Pages.
(10)	Saurel, R. and Abgrall, R., A Simple Method for Compressible Multifluid Flows, SIAM J. Sci. Comput., Vol. 21(1999), pp.1115-1145.
(11)	Shima, A. and Tomita, Y., The growth and collapse of cavitation bubbles near composite surface, Journal of Fluid Mechanics, Vol. 203 (1989), pp. 199-214.
(12)	Duncan, J. H. and Zhang, S., On the Interaction of a Collapsing Cavity and a Compliant Wall, J. Fluid Mech., Vol. 226 (1991), pp. 401-423.
(13)	Takahira, H., Numerical Analysis of Shock-Bubble Interactions with Ghost Fluid Method, RIMS Kokyuroku: Mathematical physics and applications of nonlinear wave phenomena, Vol. 1594 (2008), pp. 89-104 (in Japanese).
(14)	Kobayashi, K., Matsuno, T., Syu, S. and Takahira, H., Numerical Analysis of Shock-Bubble Interactions near Boundaries Using the Ghost Fluid Method, WIMRC 2nd Int. Cavitation Forum (Proc. Cavitation in Turbo-machinery & Medical Applications), Coventry, UK., (2008), pp. 190-196.
(15)	Kobayashi, K., Matsuno, T. and Takahira, H., Application of Multi-Grid Ghost Fluid Method to Bubble Collapse, The 14th National Symposium on Cavitation, Sendai, CD-ROM, (2009), Total 4 pages (in Japanese).