流れ 2010年9月号 目次
― 特集テーマ: 環境流体 ―
| リンク一覧にもどる | |
成層湖の流動とその数値計算
新谷哲也 |
はじめに
閉鎖性の水域である湖や貯水池では,河川と比べて移流・拡散現象が不活発であるため,富栄養化現象をはじめとした水質問題が生じやすい.その不活性化の一要因である成層化現象は水質問題のみならず,水域内の物質循環や生態系の理解を深めるために適切に把握されなければならない重要な物理現象の一つである.本稿では,湖における成層の運動と破壊現象に着目した研究とともに,筆者が開発中の環境流体モデルについて紹介を行う.
湖の成層構造とその運動について
成層化とは,外的要因によって水域内に水温や塩分濃度等の不均一が生じ,重力の作用により層状の密度構造が発達することである.水温に起因する成層は,主に太陽からの放射熱と湖・大気間の熱交換によって発達し,日本では夏から秋にかけて重力的に安定な成層構造が維持される.また,汽水湖では海から流入した塩水が底部に蓄積することで安定した塩淡成層が発達する.ここで図1に示すような湖に典型的な水温成層を考える.上層は混合層(mixed-layer)とも呼ばれ,風応力による混合が活発なため水温(密度)がほぼ均一となる.上下層の界面(躍層)付近では(負の)浮力が作用するため,界面を横切る運動量や物質の輸送が著しく抑制される.その結果として,上層部では,浅い湖のように水平方向の移流・分散性が高まり,下層部では,一般的に貧酸素化と栄養塩の蓄積による富栄養化が進行しやすい 1).
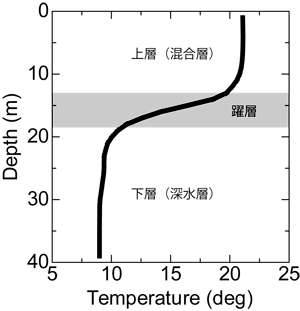
図1 典型的な温度躍層の例
成層化した湖における流動は,主に風応力で生じる吹送流と成層の固有振動現象である内部セイシュによって引き起こされる.風のエネルギーの一部は成層の傾きとして(ポテンシャルエネルギー)として蓄えられ,内部セイシュの初期エネルギーとなる(図2,実際には界面変動は水面変動より通常二桁程度大きい).吹送流は風が停止した後に短時間で減衰するが,内部セイシュによる往復振動流は風停止後も長期間継続し,水域内の物質循環に大きな影響を与える.また,台風等の強風時に風応力が成層の浮力復元力を上回ると,上述の貧酸素・富栄養の下層水が水面に達し(湧昇現象),青潮に代表される水質問題を引き起こす.これらのことから,成層の浮力復元力と風応力の関係から成層の傾きを適切に見積もることが,成層化した湖内の諸現象を理解する鍵となることがわかる.この成層の傾きを見積もるための指標として,矩形水域を仮定した無次元パラメーターWedderburn数が広く用いられてきた2).この無次元パラメーターによって,成層の傾きや湧昇限界を評価することができる.筆者らは,このWedderburn数を一般化し,地形と非線形性(有限振幅)の効果を考慮して成層の鉛直・水平変位量を見積もる修正Wedderburn数を提案している3).
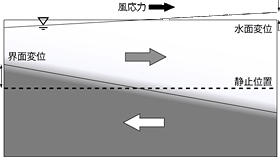
図2 風による密度界面のセットアップ(矩形水域)
上述の成層振動現象である内部セイシュは非線形性により,より短周期(高周波)の内部波に分裂することがある4).図3に矩形実験水槽内で内部セイシュから分裂する短周期内部波の数値シミュレーション結果を示す.計算は塩淡二成層の界面を傾かせた静止状態から始め,今回の条件では一周期を過ぎたあたりから明確な短周期内部波が発生する(内部セイシュの周期Tiは約94秒).この短周期内部波は,湖周辺部の斜面地形で砕波しやすく,砕波時の混合が成層水域の鉛直物質輸送に重要な役割を果たしていると考えられている.図4はその短周期内部波の砕波現象の水理実験結果を示している.砕波部先端では成層の混合現象とともにbolusと呼ばれる斜面を遡上する渦が発生し,底質の再浮上等に寄与していると考えられている5).現在も,これまで述べた風のエネルギーが最終的に成層混合へと消費されていくエネルギーカスケードプロセスについての研究が精力的に進められている6).
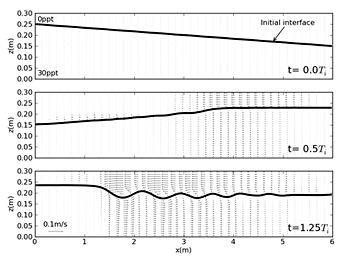
図3内部セイシュから発生する短周期内部波
(初期条件:傾斜1/60, 上層:淡水(0ppt), 下層塩水(30ppt))
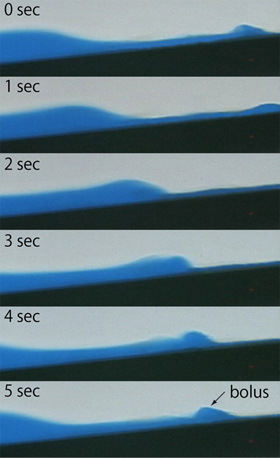
図4実験水槽内の内部波砕波現象(bolusの発生)
湖の数値計算について
はじめに湖や貯水池の流動を数値的に解析する際の主な問題点と注意点について考える.まず,湖盆地形は複雑であることが多く,合理的な水平・鉛直グリッドを作成することが難しい.そして,水域は一般的に広く浅いため,現地スケールの計算では水平方向に広い扁平な計算格子となり,計算容量・速度の関係から静水圧近似の計算を行うことが多い.そのため,短周期内部波など非静水圧・高周波現象が直接計算できず,乱流モデルにその効果を間接的に組み込まなければならない 7).また,湖の長期計算では,水温,塩分の数値拡散誤差の蓄積による成層構造の変化,運動量の数値粘性誤差による内部セイシュの数値減衰等が問題となってくる.さらに長期計算を行う際には,自由水面で発生する長波の波速によるCFL条件と鉛直方向の拡散数による時間ステップの制限回避など計算効率に関する注意も必要である.これらの問題を完全にクリアーにすることは困難であるが,高次精度スキーム,並列化,データ同化,ネスティング等の数値手法を利用し,着目する現象が合理的に再現されるように工夫を行っていく必要がある.
筆者は,上記問題の克服を目指してオブジェクト指向に基づいた流体モデルの開発を進めている8).このモデルでは,流速成分やスカラー量をはじめとした物理量,数値スキーム,計算領域など基本的な構成要素をすべてオブジェクト「モノ」として定義し,それらの詳細を気にすることはなく,積み木のように組み合わせて計算を進める.オブジェクト指向プログラミングを用いる大きな利点の一つは,動的にオブジェクトを生成・組み替えができることである.環境流体解析では,解析対象ごとに物理量の種類,数値スキーム,境界条件等が異なるため,プログラムが複雑化するか,もしくは対象ごとに専用プログラムを作ってしまうケースが多い.オブジェクト指向の機能(多態性)を用いれば,一つのプログラムが実行時に必要なオブジェクト(機能)を選択し,専用のモデルを作り上げるため,プログラムの保守性向上と無駄のない解析が同時に可能となる.
図5は本モデルの領域分割と並列化機能を用いて北海道道東に位置する汽水湖である網走湖の流動解析を行った際のスナップショットを示している.塩淡界面(白色)は風応力,地形,地球の自転の影響を受けながら周期8時間程度で振動する.次に,領域分割とネスティング(one-way)を利用した例として,内部波の砕波先端部の解析結果(上層:淡水,下層:塩水)を図6に示す.計算結果から砕波先端部に発生するbolus内の特徴的な流動と密度構造を確認することができる.
 |
 |
図5 網走湖における塩淡界面(10ppt)付近の振動流
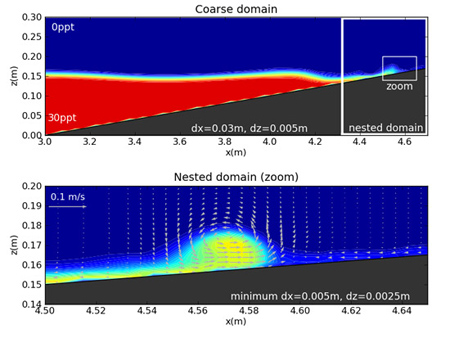
図6 斜面上における内部波砕波の数値計算
(上:大領域の密度分布,下:ネスト領域の密度・流速分布)
おわりに
本稿では湖で生じる成層化現象に関して,その運動と数値計算手法に関する研究を紹介した.内部波をはじめとした成層運動は,その様子を外から伺い知ることはできないが,水面下の物理・生物・化学過程に密接に結びついた非常に興味深い現象である.この拙稿により一人でも多くの方が,湖と成層について関心を持っていただければ幸いである.
謝辞
本稿を作成するに当たって,北見工業大学中山恵介教授にデータ提供及び助言を頂いた.また,今回の寄稿の機会を与えていただいた金沢大学木村繁男教授,長谷川雅人助教の両先生に謝意を表する.
参考文献


