流れ　2012年4月号　目次

―　特集テーマ：水素の流れ　― 巻頭言 （荻野，濱川，森本） 液体水素ピンホール漏えいと微粒化現象に関する融合型コンピュテーション 石本 淳（東北大学流体科学研究所） 水素拡散の実験的研究 井上 雅弘（九州大学） 高圧水素噴出火炎の基礎特性 武野 計二（三菱重工業） 漏洩水素ガス拡散の数値シミュレーション 松浦 一雄（愛媛大学） 　｜　リンク一覧にもどる　｜

 

液体水素ピンホール漏えいと微粒化現象に関する融合型コンピュテーション

石本淳 東北大学 流体科学研究所

１．はじめに

　 近年，液体水素(LH₂)は次世代型燃料電池自動車(FCV)の大規模な導入・普及において欠かせない極低温燃料であり，次世代型液体ロケット用推進剤，高温超電導ケーブル(HTS)用冷媒としてもその可能性を期待されている．水素を高密度に貯蔵・輸送するための要素技術の確立はこれら次世代水素応用技術開発において欠かせない重要課題である．しかし，水素の材料透過性が高く，水素接触による材料の脆化という特性により，スペースシャトル用液体水素燃料の配管材亀裂による漏えい，液体燃料貯蔵用高圧タンクからのピンホール漏えい，ボイルオフ損失や蒸発損失が問題になっている⁽¹⁾⁽²⁾．さらに，液体水素は極低温流体という性質上，蒸発速度が速いことから漏えいした場合容易に引火・大爆発を誘起する可能性を有しており，取り扱いにも注意が必要である．したがって，液体水素(LH₂)に代表される極低温流体の漏えいに伴う主要形態である，ジェット噴霧微粒化特性に関する研究は，以上に言及するような燃料電池利用型輸送機器，超伝導利用デバイス，宇宙輸送機器等の基本設計に関連して非常に重要である．ここで，水素拡散挙動に関わる実現象を予測する上でCFDを用いた解析は非常に有効な手法として期待され，ノズル入口圧・ノズル径・周囲温度等の各種流動条件をフレキシブルに変化させ，拡散挙動の数値予測をある程度の精度で行うことが可能となっている⁽²⁾．

　 水素漏えいの基本形態としては，液体状態で漏えいし蒸発した水素ガスの拡散があるが，蒸発水素ガスの挙動の最も重要な支配因子となるのが，蒸発の前段階で生じる液体水素微粒化特性と噴霧熱流動特性である⁽³⁾．最近の極低温ジェット流に関する研究としては，巨視的な液体燃料ロケットエンジンノズル流れの解析が広く行われており，また，微視的見地からの研究としては振動ノズルから噴出される単一液体水素液滴の形状と安定性について数値的な予測が行われている⁽⁴⁾．しかし，高圧タンクからのピンホール漏えいなどの水素利用安全性を評価する上で重要となる，極低温液体高速ジェット流微粒化特性に関し特に伝熱工学的影響を考慮した成果は未だ得られていないのが現状である．

　 そこで本研究では，液体水素(LH₂)の漏えい現象に関連する微小ノズルからのLH₂乱流微粒化過程，拡散挙動を解析することを目的とし，ピンホール漏えいを対象とした解析モデルを構築し，LH₂ジェット乱流微粒化特性と極低温噴霧熱流動特性に対するCFD融合数値予測を行った⁽⁵⁾．特に，LH₂液柱不安定から液膜形成と分裂を経て液滴形成に至るまで一連のプライマリブレイクアップから液滴生成に至る高速微粒化過程と噴霧温度場に及ぼす極低温熱伝達効果の影響に関して，最新のLarge Eddy Simulation - Volume of Fluid (LES-VOF) モデルを用いた詳細な融合数値解析を行ったのでその概要に関して紹介する．

 

2. 基礎方程式ならびに数値解析法

　基礎方程式のモデリングに当たっては，著者らが開発した噴霧微粒化解析用モデルに対し，混相型エネルギー式をカップリングさせ，液体水素乱流微粒化と極低温熱流動場の同時解析が可能なCFDモデルを構築するとともに，従来行われた実験条件⁽³⁾をCFD計算条件に取り入れた融合計算を行った．

　 解析対象とする流動場は液体水素(LH₂)乱流ジェット噴霧流で，基礎方程式系は一流体界面追跡型噴霧二相流を記述する方程式系を用いており，1) 質量保存の式，2) 運動方程式には表面張力項を積分項の形で含む気－液の非混合流体を統一的に扱うContinuum Surface Force (CSF)モデルに基づくNavier-Stokes方程式，3) 極低温二相流拡張型エネルギー式，さらに，4) 気相・液相を判別するインジケータ関数の移流方程式から構成される．ここで，気－液非混合のLH₂に対する微粒化流れの数値シミュレーションの実施に際しては，次の各ステップを処理する: 1)流れ場の解析，2)界面の位置を更新，3)極低温領域の温度場の解析である．1)に関しては，LES(Large Eddy Simulation)微粒化モデルによってサブグリッドスケールの微小渦領域を考慮したNavier-Stokes方程式を解く⁽⁶⁾⁽⁷⁾．2)に関しては，VOF法(Volume Of Fluid Method)を適用した解析を行う⁽⁸⁾．3)に関しては，気液ミキシングの温度場を考慮したエネルギー式を解く．

　 本融合計算においては，直径1 mmのピンホールノズルから自由噴霧領域へと高速噴出するLH₂に対し，噴霧流動特性と極低温熱流動場に関するCFD融合数値予測を行った．具体的には，LH₂ジェット流の液柱から液滴へ分裂し蒸発に至る直前まで一連の噴霧熱流動場に関し，LES-VOF法を用いた一体型非定常3次元混相乱流解析を行い，LH₂ジェット微粒化メカニズムに関する詳細な数値予測を行った．

 

3. 結果と考察

　 Fig.1は，液相体積分率Fに関する計算結果と同一実験条件下で行った可視化計測結果との比較である．ここでFig.1-(b)は，液体水素ピンホール噴霧実験⁽³⁾においてハイスピードカメラにより得られたプライマリブレイクアップから液滴形成領域におけるLH₂ジェット流微粒化の瞬間写真であり，Fig.1-(c)は，計算結果と瞬間写真を重ねて比較を行ったものである．計算結果の図と瞬間写真の縮尺は同一であり，噴孔出口位置をそろえて表示している．本融合計算結果（Fig.1-(a)）と可視化計測結果を比較するとLH₂微粒化開始からプライマリ微粒化に至る領域において，極低温流体の噴霧角が常温流体に比較して小さいという特徴が一致し，微粒化噴霧流動様式と液柱形成部の数値予測が精度よく行われていることがわかる．したがって，本数値計算の妥当性は実証されていると言える．

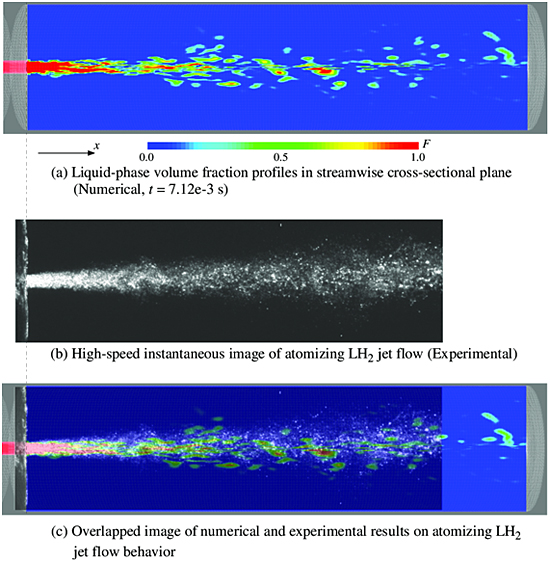
Fig.1 Comparison between numerical and experimental results for LH₂ atomizing region.

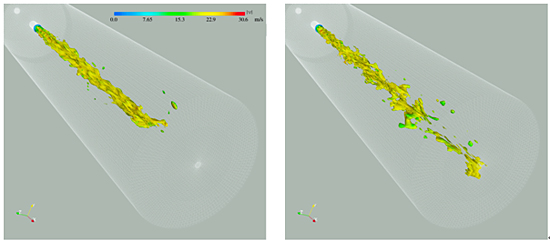
　Fig.2に，液相体積分率の瞬間等値面に関する時間発展解を示す．体積分率のしきい値はF=0.5 (気－液界面)であり，カラー階調は流速のスカラー値を表している．ノズル出口から噴出するLH₂に関し，1.) 液柱の不安定変形から分裂，2.) 液膜の形成と液膜フラグメントへの分裂・液リガメント伸張，3.) 微粒化液滴の形成までの一連の極低温流体微粒化プロセスに関する混相流動場の数値予測が効果的に達成されていることが分かる．液柱界面が波状に変形するのは，粘性の小さい極低温流体においても相間スリップに基づくKelvin-Helmholtz (K-H) 不安定が誘起されることによる．LH₂ジェット界面波の振幅は小さく波長は比較的長く現れるが，これは低粘性と小さい表面張力という極低温流体に特有の物性によると考えられる．また，LH₂ジェットの噴霧角は9.55°と，一般の常温流体ジェット流の噴霧角に比較して非常に小さい値を取ることが判明した．やがて，気液界面には界面せん断力の増大に基づく微小乱流渦が生成され，界面変形部の巻き込み現象が生じ，曲率があるしきい値を超えると液滴への分裂が生じている．微粒化が開始する領域においては渦強度が強まり，分裂後には弱まっていく．これは，渦のエネルギーが液柱の分裂と微粒化に消費されているためであり，渦強度が強まる領域においては不安定液柱の分裂が促進される．一方，LH₂液滴数密度が希薄な領域においては渦強度が減少し，微粒化促進が不活発になると考えられる．

(a) t = 1.62e-3 s	(b) t = 4.12e-3 s
Fig.2 Instantaneous iso-surface of liquid-phase volume fraction (F=0.5) with velocity scalar magnitude.

　Fig.3はノズル噴孔出口から下流側におけるLH₂ジェット噴霧流の疑似ポテンシャルコア領域（噴霧流中で流速分布がノズル出口から減衰せず一様となる領域；分裂長さ）とみなせる流体要素を示している．疑似ポテンシャルコア領域は液相体積分率が1となる領域(F =1)の等値面を抽出し全てのタイムステップ分でスーパーインポーズ（画像重ね合わせ）したものである．

　 一般に常温水のノズル噴霧においては(lp≈7d, d : nozzle diameter)程度であるが⁽⁹⁾，LH₂の場合，Fig.3に示すようにlp≈30d,であった．LH₂に代表される極低温流体は低粘性かつ表面張力が小さい物性により，ノズルスロート部通過の際に発生するせん断応力が小さく，常温流体ジェットに比較して界面不安定のスケールが小さいという特性を有するため，液柱から液滴への分裂に要する特性距離が増加し分裂長さが大きく現れるものと考えられる．

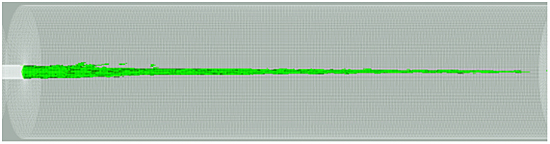
Fig.3 Potential core of liquid-phase jet flow just downstream of the nozzle aperture outlet as represented by the superimposed results of maximum liquid phase volume fraction (F=1) in all computational timesteps.

　Fig.4はLH₂噴霧流の主流方向二次元断面における温度分布Tの時間発展解である．時間進行に伴い水素液滴微粒化が活発に行われている気液界面において，LH₂ジェットから周囲流体への極低温冷却熱伝達による温度拡散が強力に促進されることがわかる．すなわち，極低温流体においては一度液柱分裂が誘起されると液柱分裂から液滴生成に至るまでの微粒化速度が速く，気液界面における接触面積が急激に増大することにより熱伝達特性が向上し，温度拡散に及ぼす噴霧微粒化の影響が大きく現れたと言える．これは，LH₂の周囲流体（気相）に対する密度比が常温流体よりも小さいため，噴霧液滴の粒子拡散効果が増大したものと考えられ，同時に温度拡散が促進されたものと考えられる．

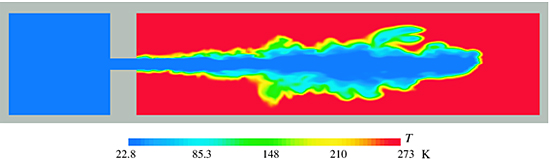(a) t = 1.62e-3 s

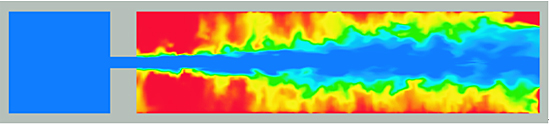(b) t = 4.12e-3 s

Fig.4 Time evolution of overall temperature T profiles in the streamwise symmetric plane.

 

まとめ

　 一連の計算結果から，常温液体とは異なる液体水素ピンホール漏えいジェットに特有の極低温噴霧微粒化特性が明らかとなった．極低温流体においては一度液柱分裂が誘起されると液柱分裂から液滴生成に至るまでの微粒化特性速度が速く，気液界面における接触面積が急激に増大することにより熱伝達特性が向上し，温度拡散に及ぼす噴霧微粒化の影響が大きく現れることを明らかにした．

　 本研究が，将来的に重要課題となり得る高圧タンク内における液体水素のピンホール漏えいに対する安全性対策に少しでも貢献することを願っている．

 

謝辞

　本稿で紹介した研究は，大平 勝秀 教授（東北大学），岡林 一木 氏（三菱重工），千歳 敬子 氏（三菱重工）との共同研究により実施した成果である．また，本研究成果に対し，Prof. Steven W. Van Sciver (NHMFL FSU, USA) より有益な助言をいただいている．ここに付記し，感謝の意を表する．

 

文献

(1)	Verfondern, K., and Dienhart, B., 1997. “Experimental and theoretical investigation of liquid hydrogen pool spreading and vaporization”. Int. J. Hydrogen Energy, 22, pp. 649–660.
(2)	Chitose, K., Okamoto, M., Takeno, K., Hayashi, H., and Hishida, M., 2002. “Analysis of a large scale liquid hydrogen dispersion using the multi-phase hydrodynamics analysis code (CHAMPAGNE)”. Trans. ASME, J. Energy Res. Tech., 124, pp. 283–289.
(3)	Nakamichi, K., Kihara, Y., and Okamura, T., 2008. “Observation of liquid hydrogen jet on flashing and evaporation characteristics”. Cryogenics, 48(1-2), pp. 26–30.
(4)	Xu, J., Celik, D., and Van Sciver, S. W., 2005. “Numerical study of liquid-hydrogen droplet generation from a vibrating orifice”. Phys. Fluids, 17, p. 082103.
(5)	Ishimoto, J., Ohira, K., Okabayashi, K., and Chitose, K., 2008. “Integrated simulation of the atomization process of a liquid hydrogen jet through a cylindrical nozzle”. Cryogenics, 48(5-6), pp. 238–247.
(6)	Apte, S. V., Gorokhovski, M., and Moin, P., 2003. “LES of atomizing spray with stochastic modeling of secondary breakup”. Int. J. Multiphase Flow,, 29(9), pp. 1503–1522.
(7)	Vinkovic, I., Aguirre, C., Simo¨ens, S., and Gorokhovski, M., 2006. “Large eddy simulation of droplet dispersion for inhomogeneous turbulent wall flow”. Int. J. Multiphase Flow,, 32(3), pp. 344–364.
(8)	Puckett, E. G., Almgren, A. S., Bell, J. B., Marcus, D. L., and Rider, W. J., 1997. “A high-order projection method for tracking fluid interfaces in variable density incompressible flows”. J. Comput. Phys., 130(2), pp. 269–282.
(9)	Lin, S. P., 2003. Breakup of liquid sheets and jets. Cambridge University Press, New York, NY.