流れ 2013年4月号 目次
― 特集テーマ:流体工学と世界No.1技術 ―
| リンク一覧にもどる | |
医療に貢献する生体力学シミュレーションに向けて
高木 周 |
1.はじめに
2012年秋より,スーパーコンピュータ「京」の共用開始が始まり,さまざまな成果が出始めている.1100億円を投じて一大国家プロジェクトとして開発された「京」コンピュータは, その演算性能が世界一となることが期待されただけでなく,当然のことながら如何にその成果が社会に還元されるかが大きく問われている.私はこれまで,生命科学の分野と関連して,2つの「京」向けのソフトウェア開発のプロジェクト(「次世代生命体統合シミュレーションに関するソフトウェアの研究開発」 http://www.csrp.riken.jp/ ,「予測する生命科学・医療および創薬基盤」http://www.scls.riken.jp/ )に関わってきた.「次世代生命体統合シミュレーションに関するソフトウェアの研究開発」では,医療応用を目指したソフトウェア開発の部分に重きが置かれ,「予測する生命科学・医療および創薬基盤」では,実際にソフトウェアを用いて大規模計算を実施し,医学・医療に対する成果を出すことを期待されている.本稿では,これらのプロジェクトの紹介を兼ね,開発してきたソフトウェアのうち,代表的なものについて紹介したい.
生体内の臓器の挙動に対するシミュレーション技術の開発は,高齢化社会においてより深刻な問題となる様々な疾患に対する高度医療を達成するため,さらには重篤な健康障害に陥らないための疾患の早期発見・早期治療にとって,重要な意味を持っている.特に,患者個々の人体の特性に合わせた個別化医療の実現に対しては,MRI, CT, 超音波などで取得された個々の人体データに基づくシミュレーションにより,病態の予測や治療の計画,治療後の経過予測などを行えるようになることが期待されている.このような背景のもと,「次世代生命体統合シミュレーションに関するソフトウェアの研究開発」のプロジェクトにおいては,医用画像データを用いた大規模流体-構造連成計算に適した計算手法(ZZ-EFSI)[1]を,また次世代型の低侵襲医療応用技術として期待が持たれている強力集束超音波シミュレータ(ZZ-HIFU)の開発などを行ってきた.以下,これらのソフトウェアについて簡単に紹介する.
2.画像データの利用に適した流体構造連成計算手法(ZZ-EFSI)
生体力学に関するシミュレーションは,筋骨格系・臓器の変形から血流まで,生体の力学に関わる動的挙動を再現し,そのメカニズムを解明すること,さらに,その結果を医療分野に応用する部分までをシミュレーションの対象としている.この際,生体力学シミュレーションに特有かつ重要となるのが,MRI,CT,超音波などの医用画像データを基にした解析である.図1に,実際に生きているヒトのMRI, CTの医用画像からコンピュータ上に再構築された全身の人体データの例を示す.全身データである必要はないが,このような医用画像データを基に病気の予測や治療の支援を行うことを考え,静的な画像データに対し,その動的挙動を表す支配方程式(質量保存式と運動量保存式など)を解くことにより,動的挙動を予測する.
生体は血流を介して細胞に酸素と栄養分を供給し,また老廃物を回収し,生命を維持している.口から入る水分や食料の移動,肺呼吸による酸素の取り込みも含め,生体を維持しているものは物質の流れである.心臓は血流を維持するポンプの役割を果たし,肺の動的挙動は酸素供給を維持する役割を果たしている.これらの例からもわかるように体内の組織・器官はいたるところで流体と接し,多くの場所で流動現象と組織・器官の形状変化が関連したものとなっている.すなわち,生体力学シミュレーションでは,血流と関連した疾患(心疾患,動脈瘤,動脈硬化・狭窄など)の再現をはじめ,様々な場面で流体構造連成の計算が必要となる.
流体構造連成問題に対して,広く用いられている数値計算手法として有限要素法がある.有限要素法では,計算の対象となる空間を有限サイズのメッシュ(要素)で埋め尽くして計算を行う.有限要素法は,数学的記述の美しさに加え,適切なメッシュ生成が行われれば,十分信頼できる結果を提供することが可能であり,実際の設計の現場でも広く用いられている.ところで,CT, MRI,超音波などにより取得された医用画像データを基にして,有限要素法による流体構造連成の問題を考えた場合には,まずは画像データのピクセル毎に与えられる輝度値などの情報から,それぞれの組織・臓器の外形の抽出さらには抽出された外形を境界に持つメッシュの生成が必要となる.このようなメッシュ生成のプロセスには,様々なノウハウが存在するため自動化が難しく,有限要素法自身の計算時間が短いものとなっても,実際に時間がかかるのは,計算を担当している人がメッシュ生成に費やす時間である場合が多い.特に,医療現場で実際に用いられる計算手法を考えた場合,メッシュ生成のノウハウを有する技術者を医療機関ごとに準備するのは困難であると考えられるため,画像データからなるべく特殊な知識を持たずにシミュレーションを行なえることが望ましい.これらのことを考慮し,医用画像データに適した流体構造連成手法の例として,界面で精度は落ちるがメッシュ生成のプロセスを必要としない固定格子を用いたオイラー型の流体構造連成の手法を開発した.図2に,物体の変形とともにメッシュ生成を行うラグランジュ型と,固定メッシュを用いながら固体の大変形を解くオイラー型の違いの説明を図示する.計算手法の詳細は,文献[1]に譲るが,ここではその手法について簡単に紹介する.

図1 コンピュータ上に構築された人体ボクセルデータ (理化学研究所より提供)
 |
 |
| (a) ラグランジュ型 | (b) オイラー型 |
| 図2 物質点に乗るラグランジュ型と,固定格子のオイラー型計算手法の違い | |
一般的に流体の運動量保存式であるNavier- Stokes方程式は,固定した格子上で計算を行うのに適しているが,大変形を伴う固体は必ずしも適した手法にならない.本研究では,臓器や細胞のように柔らかく大変形する超弾性体に対して,物質点の時間変化を,次式で表される左コーシー・グリーン変形テンソル B(=F・FT)の移流方程式を固定格子上で数値的に解くことにより追跡する新たな手法を開発した.
![]() (1)
(1)
ここで,L(=∇v) は速度勾配テンソルである.B は,対称テンソルであるため,式(1)を解くことは,6つの成分を持つ式を新たに解くことに対応する.すなわち,本手法ではメッシュ生成のプロセスを省略できる代わりに,大変形する物体の物質点の情報を維持するために,式(1)で与えられるテンソルの移流方程式を新たに解くことになる.
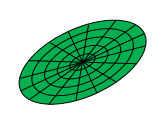
図3に計算結果の一例を示す.左上のランダムにばらまかれた超弾性体の画像データを基に,その後,流路内を左から右に変形しながら流れていく多数の弾性体を含む流れを計算した例である.本手法は固定格子を用いているため各計算ノードのロードバランスもとりやすく超大規模計算にも非常に適した手法となる.この手法は、「京」のフルノードを用いた計算で,実効速度4.5ペタフロップス(実効性能43%)の値をたたき出している.「京」がスカラー計算機であることを考慮すると,連続体の計算においてこれだけのコア数で実効性能40%以上を出しているのは,特筆すべき点である.実際に「京」を使って4.5ペタフロップのスピードを達成した計算の例を図4に示す.赤血球を模擬した300万個の超弾性体が管の中を流れていく様子が示されている.この管の中には、血小板を模擬した粒子もばらまかれており,赤血球が存在することによりその影響で血小板の拡散が誘起される様子を再現することができる(図5参照).なお,本手法の適用範囲は生体に限らず,通常の流体構造連成問題にもそのまま適用できる.画像データなどピクセルの輝度値をもとにして計算を始めるような系には特に適している.また,固い材料に対しても超弾性体の応力項を陰的に扱うことにより安定に解くことが可能となる[2].
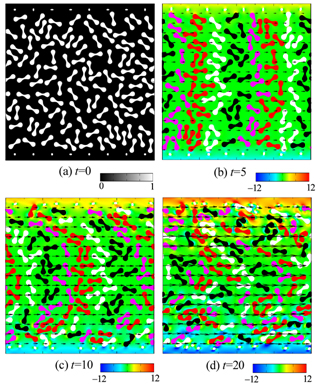
図3 ZZ-EFSIによる計算結果
(画像データから格子生成なしで計算へ)

図4 赤血球と血小板を模擬した多数の粒子を含む流れ
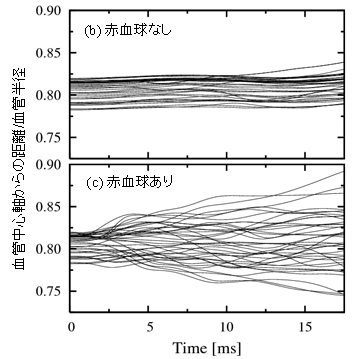
図5 赤血球の存在が血小板の拡散に与える影響
(血小板の位置の時間変化)
3.超音波治療器の開発に向けたシミュレーション(ZZ-HIFU)
高強度の超音波を患部に集束させて腫瘍の焼灼などを行うHIFU (High Intensity Focused Ultrasound) 治療が,次世代型の低侵襲治療法として期待されている.特に,欧米の企業(GE, Phillips,Siemens他)においては,脳も含めて様々な部位に対するHIFU治療機器の製品化が急速に進んでいる.これに対し日本では,従来,診断装置と比較すると治療器の開発は必ずしも積極的に推進されて来なかったが,国産初の超音波治療器開発に向け,企業と大学が連携し,日本独自の治療器の開発を進める機運にある.東京大学で進められているプロジェクト「システム失陥生命科学による先端医療技術開発拠点」TSBMI, http://www.tsbmi.m.u-tokyo.ac.jp/ においては,実際に国産初の治療器開発に向けた研究が進められており,ここで紹介するHIFUシミュレータ(ZZ-HIFU)が,治療器の性能予測のために用いられている.
HIFU治療器においては,患部(ターゲット)への超音波集束における焦点制御とターゲット以外の部位における発熱の抑制が重要となる.焦点制御の方法としては,移動する臓器等に対して画像誘導等により物理的に超音波発生部を直接動かして調整する部分と,ターゲット近傍の細かな位置制御を多数の超音波発生素子の振動の位相を制御することにより音響的な干渉を変化させ調整する部分がある.特に硬さの大きく異なる骨などが存在する場合は,軟組織との音響インピーダンスの違いにより,超音波の複雑な反射・屈折が起こり治療上の大きな障害となるため,時間反転法と呼ばれる手法を用い,アレイ状に並べた多数の超音波発生素子(トランスデューサー)の位相制御により焦点位置の制御を行う手法が考えられている.
時間反転法では,最初のステップで腫瘍の位置に仮想的に音源を起き,この音源からそれぞれの超音波素子に到達する圧力波形を記録し,この情報を用いて各素子にあたえる位相や振幅を決定する.これにより,次のステップとして,素子側から照射された超音波が,仮想的においた音源のところに集束することが期待される.しかし,実際の治療器では,有限な数の素子で有限な領域を囲み,さらに超音波伝播の非線形性の影響などにより,音源への集束は必ずしも保証されていない.実際の系でどの程度の集束が期待できるか評価するために開発されたものがHIFUシミュレータ(ZZ-HIFU)になる.このシミュレータでは,CT, MRI,超音波などで取得された医用画像と,CADデータで与えられた超音波治療器のデータを結合することにより,超音波治療における時間反転法による焦点制御の精度に関して評価することができる.
ここで紹介するZZ-HIFUは,圧力伝播に関する基礎方程式を有限差分法に基づいて空間に4次精度中心差分で離散化し,Finite Difference Time Domain(FDTD)法に準じた方法で時間積分を行っている.また,境界条件には,境界における超音波の反射を防ぐためにPerfectly Matched Layer(PML)を用いている.数値計算の詳細については,文献[4]を参照のこと.この手法を用いて,これまでも実際に生きているヒトの人体ボクセルデータを用いて,頭蓋骨越しの超音波照射や体深部にある肝臓への照射と温度上昇予測などのシミュレーションを行ってきた[4][5].ここでは,国産初の治療器の開発に向け,実際にシミュレーションを用いた評価を始めている乳がんの治療シミュレーションに関する結果を紹介する.
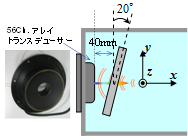
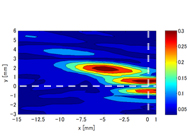
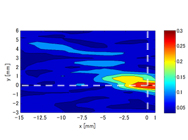
実際にどの程度,焦点制御が可能になるか評価するために行った実験について紹介する.実験は,図6(a)に示すような実験系を用いて行った.生体内の音速は,柔らかい臓器では水とほぼ同程度となり,固い骨の部分では音速が速くなる.ここでは,骨と同程度の音速を有する材料としてアクリル(音速2660m/s)を選び,図5(a)に示すように,超音波照射方向に対して,斜めに傾けた状態でアクリルの板を配置した.照射側の超音波発生装置は,56枚の素子を並べたアレイトランスデューサーとなっており,各素子の位相を別々に制御可能である.ここでは,各素子に入力する位相の情報をシミュレーションにより決定した.すなわち,まずターゲットの位置に音源を置いたシミュレーションを行い,そのシミュレーション結果から各素子に与える位相の情報を決定した.その後,その位相情報を実験側の入力シグナルとして与え,超音波照射の実験を実施し,ニードルハイドロフォンを空間的にスキャンして,3次元音場計測を行った.超音波の照射方向にターゲットを含む断面における音場の実測結果を図6(b),(c)に示す.(b)は位相制御をせずに同位相で照射した場合で,この場合には,ターゲットに集束していないだけでなく,ターゲット以外の場所に3カ所ほど圧力の高い部分が現れている.このようなことが実際の治療で起きた場合には,正常な部位を焼灼してしまうこととなる.これに対し,時間反転法のシミュレーション結果を利用して,位相制御を行った結果を図(c)に示す.位相制御を行うことにより,ターゲットのところに超音波集束が達成されているのがわかる.
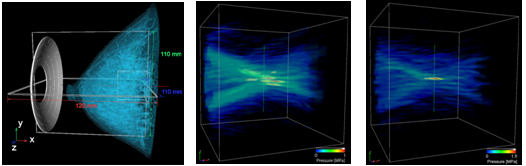
上記の例は,単純な実験系であるが,実際の人体のように複雑な形状を持つ多媒質体に対しても,このようにシミュレーション情報を利用して位相制御を行うことにより焦点制御が可能となる.実際に実用化に向けて検討を開始している乳がんの治療に関するシミュレーションの結果を図7に示す.図は,乳房の画像データをもとに脂肪と乳腺の判別を行い構築した計算系である.乳房の場合には,脂肪と乳腺組織はどちらも軟組織であり,ここでは文献値に従い音速を1547[m/s]と1465[m/s],音響インピーダンスで1597[kg/m2s],1443[kg/m2s]とそれぞれ,与えている.骨(音速3000~4000[m/s]程度)と比較すると均質な媒質とみなして良いような印象を与えるが,実際にシミュレーションを行ってみると,位相制御を行わない場合には,超音波が焦点に集束せずに3箇所のピーク値を持っているのが(b)図よりわかる.これに対して,(c)図より時間反転法による位相制御を行うことによりターゲットの位置に超音波が集束しているのがわかる.
さて,実際に治療をする場合には,超音波の集束位置,温度分布および焼灼程度のモニタリングすることが重要となる.世界的には,MRIにより温度モニタリングをしながら腫瘍の焼灼を進めるMRI-Guided HIFUによるものが主流となりつつある.これに対し,現在,我々が開発を進めている超音波治療器は,超音波でリアルタイムに観察しながら超音波で焼灼する方法である.この装置を実現させるために,腫瘍への集束および焼灼程度を判定するための診断プローブを組み込んだ診断・治療一体型のHIFU治療器の開発を行っている.すなわち,焦点位置を高精度に制御し,かつ焼灼程度を判定するのに十分な解像度を持つ装置の開発を進めており,上記のHIFUシミュレータを用いた大規模シミュレーションにより超音波素子の配置および診断プローブのための開口径の検討なども行っている.
 |
 |
 |
| (a) 実験装置概略図 | (b) 位相制御なし | (c) 位相制御あり |
| 図6 シミュレーション結果を利用した実験による検証 | ||
 |
||
| (a) 画像データから構築された シミュレーション系 |
(b) 焦点制御なしの場合 (焦点以外で高い圧力) |
(c) 焦点制御ありの場合 (焦点近傍のみで高い圧力) |
| 図7 乳ガン治療を対象としたシミュレーション | ||
4.おわりに
「京」の共用開始が始まり,いよいよ生体力学に関するペタフロップス級の超大規模計算が開始される.本稿では,「京」向けに順次公開を進めているソフトウェアの一部を紹介し,研究開発の現状と今後の展望を説明した.また,本稿で紹介したオイラー型流体構造連成を発展させ流体-膜連成問題へと適用できるようにした手法に,タンパク質分子レベルからの相互作用を考慮にいれたマルチスケール血栓シミュレータや東京大学の久田俊明らにより開発が進められているマルチスケール・マルチフィジックス心臓シミュレータ(UT-Heart),全身の血管網モデルなどについては,文献[7]にて説明を行った.興味を持たれた読者は参照されたい.開発されたソフトウェアのいくつかは,今回紹介できなかったものも含め, http://www.csrp.riken.jp/application_j.html のサイトに順次,公開されていく.ぜひ,多くの方にご利用して頂きたい.
謝辞
流体構造連成手法(ZZ-EFSI)は,杉山和靖博士(理研),超音波シミュレータZZ-HIFUは,沖田浩平博士(日大)が実際の並列計算用のソフトウェアの開発を行っている.記して感謝の意を表する.
参考文献


