流れ　2018年3月号　目次

―　特集テーマ：第9回日韓熱流体工学会議(TFEC9)　― 巻頭言 （橋本，松田，朴） 平板上の遷移境界層における乱流の始まり 福西 祐，西尾 悠，伊澤 精一郎（東北大学）吉川 穣（宮城県産業技術総合センター） E-MPS法を用いた単一溶融液滴の凝固・付着シミュレーション 近藤 真一郎，守 裕也（東京理科大学）福島 直哉（東海大学）山本 誠（東京理科大学） PM2.5の帯電状態測定のための平行平板粒子分級器の数値シミュレーション 米道 卓音，深潟 康二，藤岡 謙太郎，奥田 知明（慶應義塾大学） 粘弾性流体中における鞭毛螺旋模型の推進力特性に与える粘弾性マッハ数の影響 田島 和哉，三神 史彦（千葉大学） 可変マイクロギャップ電極を用いたイオン電流場の計測 福田 敬志，土井 謙太郎，川野 聡恭（大阪大学） 　｜　リンク一覧にもどる　｜

 

粘弾性流体中における鞭毛螺旋模型の推進力特性に与える粘弾性マッハ数の影響

田島 和哉 千葉大学大学院， 三神 史彦 千葉大学

1.　緒言

　平成29年10月に沖縄コンベンションセンターで開催された第9回日韓熱流体工学会議において優秀講演賞を頂き，大変光栄に存じます．本稿では，対象となった講演発表⁽¹⁾の概要を紹介いたします．

　遊泳能を持つ原核生物は，螺旋状の鞭毛を剛体的に回転させて鞭毛の螺旋波を後方に伝播させることで推進力を得ており（図1），螺旋波の伝播速度は数mm/sに達するものもある⁽²⁾．鞭毛による推進は，通常，ニュートン流体中のストークス流れを仮定して解析が行われるが⁽³⁾，ヒトの胃に生息する細菌Helicobacter pyloriが胃粘液の中で運動するなど⁽⁴⁾，多くの微生物はバイオフィルムや生体内の粘膜などの粘弾性やシアシニング性を示す流体中を遊泳している⁽⁵⁾．このような流体中で鞭毛螺旋が発生する推進力を調べた研究が最近増えてきているが⁽⁶⁾⁽⁷⁾，流体の粘弾性が推進力特性に与える影響については，まだよくわかっていないことが多い．

　粘弾性流体の特徴の一つに，流体中を横波のせん断波が伝播することがあげられるが⁽⁸⁾，これまで行われてきた研究⁽⁶⁾⁽⁷⁾では，せん断波の影響について考慮されることがなかった．せん断波の伝播速度は剛性率が1 Pa程度の希薄溶液中では数mm/sであり，鞭毛の螺旋波の伝播速度と同程度である．せん断波の伝播速度に対する代表速度の比は粘弾性マッハ数と呼ばれるが，一様流中におかれた物体まわりの流れの線形理論による解析では，支配方程式はM > 1のとき双曲型，M < 1のとき楕円型となることが知られており，M > 1のときには物体のまわりにせん断波マッハコーンが形成されることが示されている⁽⁸⁾．せん断波マッハコーンの形成はまた，実験的にも確認されている⁽⁹⁾．

　そこで，鞭毛の螺旋波の伝播速度を代表速度とする粘弾性マッハ数が，鞭毛の発生する推進力特性に対して重要なパラメータとなっているのかどうかについて調べたのが本研究である．図2に示すような異なるピッチや巻き径，線径をもつ7種類の鞭毛螺旋模型を用いて，回転数を変化させながら粘弾性流体中で推力測定と流れ場のPIV（Particle Image Velocimetry）計測を行い，粘弾性マッハ数が鞭毛螺旋の推力と周囲の流れ場に与える影響を明らかにした．

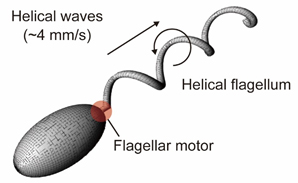
Fig.1  Flagellar propulsion by helical waves.

 

2.　実験方法

　本研究では，CTAB/NaSal系のひも状ミセル水溶液を実験に用いた．界面活性剤CTABのモル濃度30 mM，40 mM，50 mM に対して，ひも状ミセル形成のために添加する塩NaSalのモル比は4とした．また，実験流体には可視化のためのトレーサ粒子として，水性アクリル絵具（蛍光レッド）を溶液中に混入した．せん断波伝播速度の実測値は30mM，40 mM，50 mMの順に，72.9 mm/s，96.5 mm/s，114.2 mm/sであり，粘弾性マッハ数の算出に用いた．

　推力測定のための実験装置の概略を図3(a)に示す．推力測定はLiuら⁽⁶⁾ の手法に基づいている．円筒形のポリ塩化ビニル容器（直径80 mm，高さ146 mm）に実験流体を満たし，感度100 μNの電子天秤（A&D社，GF-8K2）の中央に設置した．ステッピングモータ（シナノケンシ社，CSA-US）に取り付けた鞭毛螺旋模型を鉛直に10ピッチ分流体中に浸し，角速度Ωで回転させた．それぞれの設定角速度について，電子天秤の値が定常となった10秒間の平均値を螺旋模型の推力とした．

　PIV計測のための実験装置の概略を図3(b)に示す．実験流体を透明アクリル製容器（底面100 mm×100 mm，高さ200 mm）に満たし，ステッピングモータに取り付けた鞭毛螺旋模型を鉛直に10ピッチ分液体中に浸し，角速度Ωで回転させた．照明には，Nd:YAGレーザー（532 nm, 30 mJ/pulse）のシート光を用いた．可視化した流れはシャープカットフィルタ（O56）を取り付けたCCDカメラ（Vieworks VA-4M, 2336×1752 pixel）で撮影し，相互相関法PIVを用いて速度場を算出した．

Fig.2  The helical flagellum models used for this study.

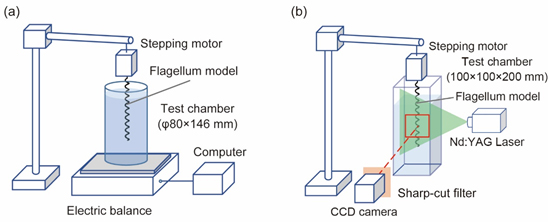
Fig.3  Experimental setups for (a) thrust measurement and (b) PIV measurement.

 

3.　結果および考察

時刻tにおける螺旋模型の中心線形状は，kを螺旋に沿う波数，Ωを回転角速度，bを螺旋半径とすれば，sを弧長パラメータとして，

のように表すことができる⁽³⁾．図4に，螺旋の接線速度Ω / kと単位弧長当たりの推力F / Lの関係を示す．ここで，Fは推力の測定値，Lは螺旋模型の液体中の弧長である．200 mm/s以上の高い接線速度では，螺旋模型の形状や溶液の濃度によらず，単位弧長当たりの推力は接線速度Ω / kのみに依存して決まることがわかった．また，単位弧長あたりの推力の回転数依存性が F / L ∝ Ω^1/2からF / L ∝Ω²へと変化する臨界値が存在し，その臨界値は螺旋模型の形状や溶液の濃度（すなわちせん断波の速度）によって異なっている．そこで我々は，螺旋回転軸方向の粘弾性マッハ数M_x = v_x/cに着目した．ここで，v_xは螺旋波の伝播速度，cはせん断波の伝播速度である．この軸方向粘弾性マッハ数M_xと単位弧長当たりの推力で図4を整理しなおしたのが図5である．ほとんど全ての条件において，M_x =1を境に軸方向粘弾性マッハ数に対する推力の増加傾向が変化しており，グラフの傾きが常に1となるニュートン流体とは全く異なった推力特性を示すことがわかった．

　次に，推力の回転数依存性の変化と流れ場の変化との関係を明らかにするため，螺旋模型周囲の流れのPIV計測を行った．図6に，螺旋模型（Model-E）をCTAB 30 mM水溶液中で回転させたときの，回転軸に沿った断面内速度の軸方向成分を示す．青色は下向きの流れを示し，赤色は上向きの流れを示している．白く抜けた部分は，速度ベクトルが算出できなかった点である．上段4枚のM_x < 1の条件では，螺旋模型を挟み左右非対称の流れが発生しているが，下段4枚のM_x > 1の条件では，左右対称の流れが発生した．このような，亜臨界流れ（M_x < 1）と超臨界流れ（M_x > 1）での流れ場の顕著な違いが，M_x = 1 での推力の回転数依存性の急変を引き起こしたと考えられる．

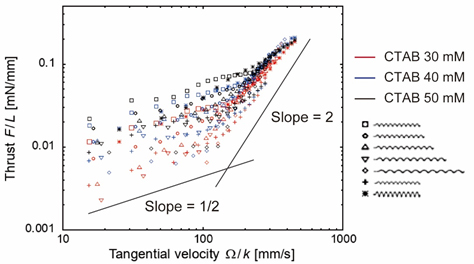
Fig.4  Thrust per unit filament length vs. tangential velocity.

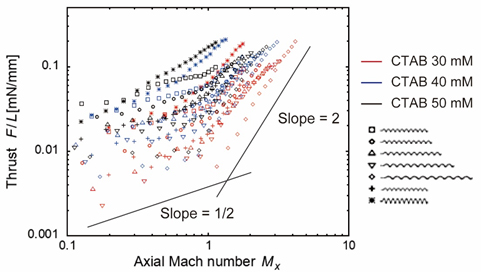
Fig.5  Thrust per unit filament length vs. axial Mach number.

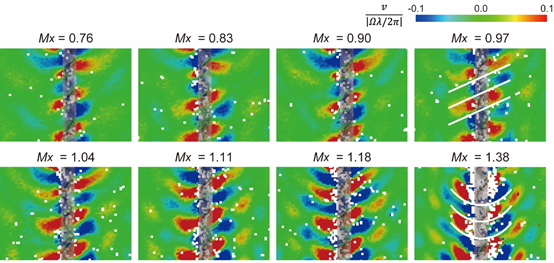
Fig.6  The axial component of fluid velocity generated by a rotating helical model (Model-E, 30mM).

 

4.　結言

　粘弾性流体中で回転する鞭毛螺旋模型が発生する推力特性を，CTAB/NaSal系のひも状ミセル水溶液を用いて実験的に測定した．その結果，推力の回転数依存性が急変する臨界値が存在することがわかり，せん断波の伝播速度に対する螺旋波の伝播速度で定義した軸方向粘弾性マッハ数M_x = 1がその臨界値であることを示した．さらにPIV計測によって，鞭毛螺旋周囲の流れ場が，亜臨界流れ（M_x < 1）と超臨界流れ（M_x > 1）で大きく変化することがわかった．これらの結果は，粘弾性流体の低レイノルズ数流れにおいても，せん断波の波動現象を考慮することの重要性を示唆している．

その後，各種高分子水溶液でも実験を行い，せん断波の減衰が小さい溶液ほど上記の特徴がよく現れるという，波動現象の重要性を裏付ける結果を得ている ⁽¹⁰⁾．

 

謝辞

　本研究は JSPS科研費JP15K065784の助成を受けました．最後に，選考委員会の皆様，ならびにニュースレター執筆の機会を与えてくださいました日本機械学会流体工学部門の関係の皆様に感謝申し上げます．

 

文献

(1)	Tajima, K., and Mikami, F., Effect of viscoelastic Mach numbers on propulsive forces of a model helical flagellum in a viscoelastic fluid, TFEC9 (Okinawa, Japan), Extended Abstracts, (2017), TFEC9-1077.
(2)	Brennen, C., and Winet, H., Fluid mechanics of propulsion by cilia and flagella, Annual Review of Fluid Mechanics, (1997), pp.354-370.
(3)	Lighthill, J., Flagellar hydrodynamics, SIAM review, 18(2), (1976), pp.161-230.
(4)	Celli, J. P., et al., Helicobacter pylori moves through mucus by reducing mucin viscoelasticity, Proceedings of the National Academy of Sciences, 106(34), (2009), pp.14321-14326.
(5)	Rodenborn, B., Chen, C., Swinney, H. L., Liu, B., Zhang, H. P., Propulsion of microorganisms by a helical flagellum, Proceedings of the National Academy of Sciences, 110(5), (2013), pp.E338-E347.
(6)	Liu, B., Powers, T. R., Breuer, K. S., Force-free swimming of a model helical flagellum in viscoelastic fluids, Proceedings of the National Academy of Sciences, 108(49), (2011), pp.19516-19520.
(7)	Spagnolie, S. E., Liu, B., Powers, T. R., Locomotion of helical bodies in viscoelastic fluids: Enhanced swimming at large helical amplitudes, Physical Review Letters, 111(6), (2013), pp.1–5.
(8)	Joseph, D. D., Fluid dynamics of viscoelastic liquids, Springer-Verlag, (1990), pp.164-176.
(9)	Mikami, F., Yagi, Y., Mach cones in a viscoelastic fluid, ICTAM2016 (Montreal, Canada), Book of Papers, (2016), pp.1272–1273.
(10)	田島和哉・三神史彦，”粘弾性を持つ各種流体中における鞭毛螺旋模型の推進力特性”, 第30回バイオエンジニアリング講演会講演論文集, (2017), 1I02.