流れ　2019年3月号　目次

―　特集テーマ：流体工学部門講演会　― 巻頭言 （橋本，松田，朴） 民間単独での観測ロケット開発と打上げとその後の超小型衛星打上げロケット開発状況 稲川 貴大（インターステラテクノロジズ株式会社） 一様吹出し制御による翼面摩擦抵抗低減効果の実験的定量評価 江藤 薫子，近藤 佑亮，深潟 康二（慶應義塾大学），徳川 直子（宇宙航空研究開発機構） 受動吹出し制御による翼面摩擦抵抗低減の風洞実験 廣川 詩歩，江藤 薫子，近藤 佑亮，深潟 康二（慶應義塾大学），徳川 直子（宇宙航空研究開発機構） 翼に渦が干渉する場合の翼周りの流れと発生する空力騒音に関する研究 小林 典彰（東京大学） 遷音速多段軸流圧縮機における静翼列流れのLES解析 齋藤 誠志朗（九州大学） WALEモデルを用いた円管内乱流のLESにおける格子解像度の影響 岩佐 大器，難波江 佑介，深潟 康二（慶應義塾大学） 流れの夢コンテストに参加して 寺田 智美（北海道大学）   水面制御装置を用いたゴミの分別 本間 俊貴（明星大学） 　｜　リンク一覧にもどる　｜

 

受動吹出し制御による翼面摩擦抵抗低減の風洞実験

廣川 詩歩 慶應義塾大学	江藤 薫子 慶應義塾大学	近藤 佑亮 慶應義塾大学	深潟 康二 慶應義塾大学	徳川 直子 宇宙航空研究開発機構

1.　はじめに

　第96期流体工学部門講演会において発表⁽¹⁾を行い，光栄にも日本機械学会流体工学部門優秀講演表彰を頂きました．この場をお借りして日本機械学会流体工学部門の皆様に御礼申し上げます．本ニュースレターでは，講演発表の内容である受動吹出し制御による翼面摩擦抵抗低減の風洞実験について紹介させていただきます．なお，本研究の先行テーマである，外部からの空気供給を用いた能動的な一様吹出し制御に関しては，本ニュースレターの別記事⁽²⁾をご覧下さい．

2.　背景および目的

　近年，航空機のエネルギー効率の向上がより一層重要な課題となっており，航空機にかかる流体抵抗のうち未だ実用的な低減手法の確立には至っていない摩擦抵抗を低減することが求められている．

　一様吹出し制御はこの摩擦抵抗を低減する手法の一つとして知られており，平板乱流境界層において壁面から微小な速度で流体を吹出すことによって摩擦抵抗が効果的に低減されることが先行研究によって報告されてきた^(3,4,5)．平板における吹出し制御以外にも，翼面における摩擦抵抗低減を目的とした吹出し制御について研究がなされている．Liu et al.⁽⁶⁾ は RANS を用いて RAE2822 翼における吸込みと吹出しを組み合わせた制御の効果を調査し，前縁で吸込みながら後縁上面で吹出す制御によって最大で16% の抵抗低減効果を報告した．また，Eto et al.⁽⁷⁾ は，翼型に対する能動的なUB 制御の摩擦抵抗低減効果の実験的評価を行い，翼上面後縁におけるUB 制御によって摩擦抵抗が低減されることを確認した．さらにこの実験では，翼面の圧力差を利用した受動的なUB 制御の実現可能性が示唆された．

　このように，数値シミュレーションと実験により能動的なUB制御の摩擦抵抗低減効果の検証がなされ，同時に，外部からのエネルギー供給を必要としない受動的な吹出し制御の実現可能性が示唆された．そこで本研究では，翼面にかかる圧力差によって駆動される受動的な吹出し制御（Fig. 1）による摩擦抵抗低減効果を，風洞実験を通じて評価することを目的とする．

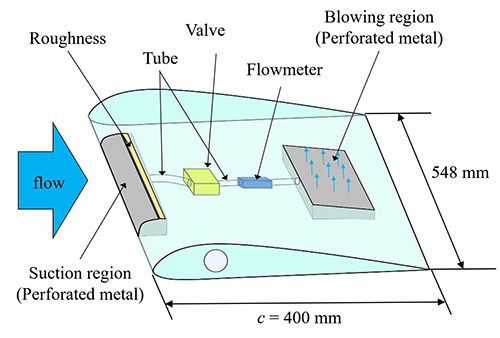
Fig. 1: Schematic of passive blowing.

Fig. 2: Clark-Y airfoil model.

3.　実験手法

　実験はJAXA航空技術部門の65 cm×55 cm小型低乱風洞で実施し，熱線流速計を用いて境界層の速度分布計測を行った．本研究の受動吹出し制御のために試作したClark-Y翼模型をFig. 2に示す．前縁に吸込み領域，上面の後縁側に吹出し領域が設置されており，これら二つの領域間の圧力差によって受動的な吹出しが実現される機構となっている．吸込み領域と吹出し領域の翼面には，ピッチ1.0 mm の60度千鳥格子状に直径0.5 mmの孔が穿孔されたパンチングメタルを用いた．また，乱流摩擦抵抗低減制御が必要なときにのみ吹出しを行うスイッチング機構⁽⁸⁾として，吸込み口と吹出し口を繋ぐチューブ間に，吹出しのon/offを切り替えるための電磁バルブを設置した．

　実験条件は迎角αを0°と6°とし，コード長cに基づくレイノルズ数Re_cを0.65 × 10⁶と1.55 × 10⁶とした．それぞれの試験条件で，スパン方向中央断面の吹出し制御領域において制御時と非制御時の境界層速度分布計測を行った．以下では，非制御時をnb，制御時をwb と表すこととする．

4.　結果および考察

　Figure 3に主流方向位置x / c = 0.70の主流方向平均速度分布を示す．この図から，制御によって境界層速度分布が翼面から遠ざかる方向にシフトしており，翼面での速度こう配が減少していることが示唆される．先行研究^(4,5) においても，このような変化がみられる場合に壁面近傍での速度こう配が減少し，摩擦抵抗が低減されることが確認されていることから，受動的な吹出し制御による摩擦抵抗低減効果が定性的に確認された．

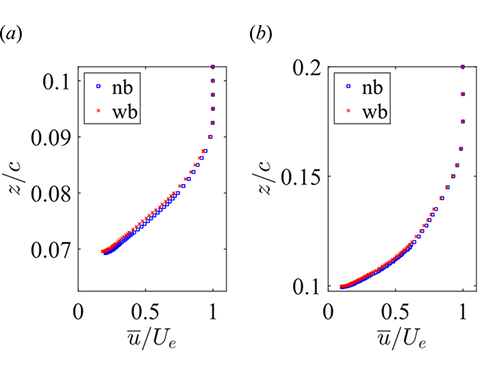
Fig. 3: Mean velocity profiles at x / c = 0.70:
(a) α = 0°, Re_c = 1.55 × 10⁶; (b) α = 6°, Re_c = 1.55 × 10⁶.

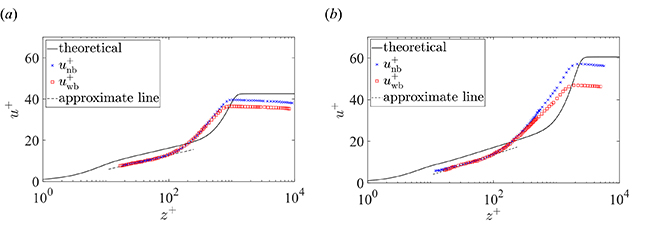
Fig. 4: Non-dimensionalized mean velocity profiles at x / c = 0.70:
(a) α = 0°, Re_c= 1.55 × 10⁶; (b) α = 6°, Re_c = 1.55×10⁶.

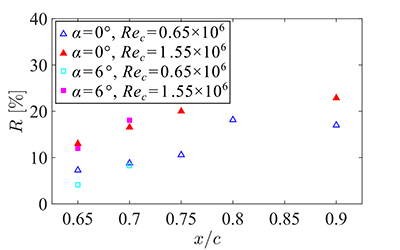
Fig. 5: Local friction drag reduction rate R.

　境界層平均速度分布の結果に基づき，摩擦抵抗低減効果を定量的に評価した．本研究では，圧力こう配に加え，壁面粗さを加味した定量評価に取り組んだ．なお，ここでの壁面粗さは，制御領域において吹出しのために使用しているパンチングメタルによるものである．乱流境界層の主流方向平均速度分布は壁面粗さの影響を受けることで，壁指標において対数則領域における傾きは滑面の速度分布に等しいまま，無次元化した速度 u⁺ が減少する方向にシフトすることが知られている⁽⁹⁾．そこで壁指標で表した速度分布の対数則領域において，Nickels⁽¹⁰⁾の圧力こう配を考慮した平均速度分布の傾きと，実験結果の平均速度分布の傾きを比較する．このとき，理論式の傾きに対し，実験結果の傾きを最も良く一致させる摩擦速度を求める．なお，吹出し制御により境界層速度分布が一般的な壁法則に従わなくなることから，Vigdorovich⁽¹¹⁾による修正Stevenson則を用いて制御時の速度分布に補正を施している．Figure 4に，以上の過程から求まった摩擦速度によって無次元化した境界層速度分布を示す．この定量評価により求まった非制御時の摩擦速度と，制御時の摩擦速度を用いて定義される局所摩擦抵抗低減率R の分布をFig. 5に示す．この定量評価の結果，制御領域における局所摩擦抵抗低減率は，4%-23%と見積もられた．

5.　おわりに

　本研究では，翼における受動的な吹出し制御による摩擦抵抗低減効果を風洞実験によって評価した．主流方向平均速度分布が吹出し制御により壁面から遠ざかる方向に変化していることから壁面における速度こう配の減少が示唆され，定性的に摩擦抵抗低減効果が確認された．また，外部からの空気供給を用いた能動的な吹出し制御⁽²⁾の場合と比べて効果は小さいものの，圧力こう配および壁面粗さを考慮した定量評価の結果，4%-23%の摩擦抵抗低減効果が確認された．

謝辞

　本研究はJAXA-慶應義塾共同研究「境界層制御による航空機の抵抗低減に関する研究」の一環として実施されました．またJSPS科研費JP16K06900の助成を受けたものです．また，末筆となりますが，ご指導頂きました慶應義塾大学　小尾晋之介教授，安藤景太専任講師ならびに当日会場にて貴重なご質問を頂きました皆様に深く感謝申し上げます．

参考文献

(1)	廣川詩歩，江藤薫子，近藤佑亮，深潟康二，徳川直子，「受動吹出し制御による翼面摩擦抵抗低減の風洞実験」，日本機械学会第96期流体工学部門講演会，室蘭，2018年11月29日-30日，Paper OS1-13 (2018).
(2)	江藤薫子，近藤佑亮，深潟康二，徳川直子，「一様吹出し制御による翼面摩擦抵抗低減の実験的定量評価」，日本機械学会流体工学部門ニュースレター「流れ」，2019年3月号，Article No. 3 (2019).
(3)	Park, J. and Choi, H., “Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer flow, Physics of Fluids,” Vol. 11, No. 10, pp. 3095-3105 (1999).
(4)	Kametani, Y. and Fukagata, K., “Direct numerical simulation of spatially developing turbulent boundary layers with uniform blowing or suction,” Journal of Fluid Mechanics, Vol. 681, pp. 154-172 (2011).
(5)	Kondo, Y. and Fukagata, K., “Friction drag reduction of a spatially developing boundary layer with pressure gradient by uniform blowing and suction,” 11th European Fluid Mechanics Conference, Seville, Spain, Sept. 12-16, 2016 (2016).
(6)	Liu, P. Q., Duan, H. S., Chen, J. Z. and He, Y. W., “Numerical study of suction-blowing flow control technology for an airfoil,” Journal of Aircraft, Vol. 47, No. 1, pp. 229-239 (2010).
(7)	Eto, K., Kondo, Y., Fukagata, K. and Tokugawa, N., “Friction drag reduction on a Clark-Y airfoil using uniform blowing,” 2018 Flow Control Conference, AIAA AVIATION Forum, Atlanta, June 25-29, 2018, AIAA Paper 2018-3374 (2018).
(8)	国立開発研究法人宇宙航空研究開発機構（徳川 直子），学校法人慶應義塾（深潟 康二，近藤 佑亮，江藤 薫子，廣川 詩歩），「気流制御装置，航空機および気流制御方法」，特願2018-029486.
(9)	White, F. M., Fluid Mechanics Seventh Edition in SI Units, McGraw-Hill (2011), pp. 377-379.
(10)	Nickels, T. B., “Inner scaling for wall-bounded flows subject to large pressure gradients,” Journal of Fluid Mechanics, Vol. 521, pp. 217-239 (2004).
(11)	Vigdorovich, I., “A law of the wall for turbulent boundary layers with suction: Stevenson's formula revisited,” Physics of Fluids, Vol. 28, 085102 (2016).