流れ 2019年3月号 目次
― 特集テーマ:流体工学部門講演会 ―
| リンク一覧にもどる | |
翼に渦が干渉する場合の翼周りの流れと発生する空力騒音に関する研究
 |
| 小林 典彰 東京大学 |
1.概要
日本機械学会第96期流体工学部門講演会において私の研究発表が優秀講演表彰に選ばれたことを大変光栄に思っております.本稿ではこれまで行ってきた研究の概要についてご紹介いたします.
空力騒音は一般には風切り音とよばれ,自動車のドアミラー,新幹線のパンタグラフ,航空機の主翼・主脚などの輸送機械や空調機器のファン,風車翼などの流体機械から発生する,空気の流れに起因する騒音で,工学的に重要な問題となっています.本研究では翼から発生する空力騒音(翼騒音)について扱っています.
翼騒音に関しては古くから研究されており,Brooks(1)らがそのメカニズムをまとめたものが知られています.ここでは,翼騒音を5種類に分類していますが,翼面境界層が大きく剥離したり,翼が失速したりしておらず,翼が揚力を発生している場合,主として問題となるのは乱流境界層・後縁騒音とよばれる広帯域騒音です.広帯域騒音は,翼表面に生じる乱流境界層内の乱れが後縁を通過するときに翼の後縁で音波が散乱されることにより発生します.
乱流境界層・後縁騒音に関しては,翼に流入する主流の乱れは小さいものと仮定し,純粋に翼自身から発生する騒音について,風洞実験や数値流体解析を用いて研究されています.一方,実際に翼が用いられる状況を考えると,たとえば,風車は地形の影響を受ける大気境界層の中に置かれたり,ウィンドファームなどでは風上側の風車の後流の影響を受けたりします.また,空調用のファンでもダクト内に置かれたさまざまな物体により乱れた気流が翼に流入する場合があります.このため,乱れた流れの中に置かれた翼から発生する騒音について考慮することも重要です.この乱れと翼騒音との関係についてはAmiet(2)が研究しており,流入する乱れから発生した音波が翼の前縁で散乱することで大きな音が放射されるとしています.しかし,主流乱れの影響を受ける翼から発生する音に関してはまだ十分には解明できていませんでした.
そこで,本研究ではまず,動的乱流発生装置を用いた風洞実験を行い,乱れ強度を10~20 %,乱れのスケール(積分長スケール)を翼弦長の2倍~10倍の範囲で変化させた場合の翼から発生する空力音と翼面静圧を計測しました.その結果,乱れにより主流の流速変動スペクトルは広周波数帯域で増大し,そのときの翼から発生する音の音圧レベルも同じ周波数帯域で増大することを示しました(3).また,翼面静圧に関しては,翼の前縁(負圧面,圧力面ともに)に強い変動があることがわかりました.また,主流の乱れ強度が境界層の乱れ強度(最大10%程度)より高い場合は,翼の後縁まで主流乱れの影響が残ることがわかりました(4).次に,発生する音や後流の特性がよく知られている円柱に着目し,直径が翼弦長の4.0~6.7 %の円柱を翼の上流に設置し,このときに生成されるカルマン渦を翼と干渉させ,単一スケールの渦が局所的(翼面近傍などに)に流入する場合において,発生する空力音と翼面静圧を計測する風洞実験を行いました.この実験では,渦の発生周波数(円柱の直径)の影響に加えて,渦の流入位置が発生する音に与える影響を調べました.その結果,翼の淀み点付近にカルマン渦が流入すると,翼負圧面の境界層がバイパス遷移するとともに,カルマン渦のピーク周波数以外の広周波数帯域で翼から発生する音が増大するのに対して,それ以外の場所に渦が流入した場合は,カルマン渦が翼面の流れと翼から発生する音に与える影響は小さいことが明らかになりました(5).
最後に,本研究ではこのような現象をより詳細に明らかにするため,Large Eddy Simulation(LES)による数値流体解析と空力音響解析を行い,乱れ(渦)が干渉するときの翼周りの流れと発生する空力騒音との関係について調べました.以下では,特に,円柱の後流と翼とを干渉させた場合の実験装置,数値解析手法,ならびに,主要な結果を示します.
2.風洞実験手法および数値解析手法
2.1.低騒音風洞および翼模型
本研究では図1に示す回流式の低騒音風洞を使用しました.吹き出し口寸法は0.5 m×0.5 m,測定部の長さは1.7 mで上下に端板を設置した,側壁のないセミオープンタイプの風洞となっており,測定部は無響室の中に設置されています.風速40 m/sにおける風速の非一様性は1.0 %以内,気流の乱れは0.5 %以内です.暗騒音レベルは同風速において,気流中心から1 mの位置で56 dB(A)です.また,使用した翼模型は2次元形状の対称翼NACA0012で,翼弦長は150 mm,翼幅長は500 mmです.翼模型は実効迎え角が9°となるように,吹き出し口から300 mm下流側にある風洞測定部のターンテーブル上に設置しています.このターンテーブルの中心から側方1 mの位置に1/2インチマイクロフォンを設置して空力騒音を計測しました.また,翼模型の負圧面・圧力面に静圧孔(平均静圧計測用)を40孔,負圧面に半導体型圧力センサを内蔵した静圧孔(静圧変動計測用)を16孔設けています.平均静圧孔はアンプ内蔵型の圧力変換器に接続され,また,変動静圧孔の圧力センサの出力はアンプに接続し,平均静圧と変動静圧を全孔同時に計測しています.風速を翼面静圧計測時は20 m/sに,また,空力音の計測時は30 m/sにそれぞれ設定しました.翼弦長を代表長さとした,それぞれの計測条件におけるレイノルズ数は,2.0×105,3.0×105となっています.

Fig. 1 Experimental set-up of test section
2.2.円柱模型とその設置位置
円柱から放出されるカルマン渦のストローハル数は約0.2であることが知られており,円柱を翼の上流に設置することで,翼に対して単一スケールの渦を流入させました.円柱模型は直径d=6 mmで,実験風速30 m/sにおけるピーク周波数は1000 Hz,渦スケールは4.77 mm(翼弦長の約3%)と推定され,円柱の直径を代表長さとしたレイノルズ数は1.2×104となります.後述するLES解析の結果(図2)から,円柱は翼前縁の中心から100 mm上流側の地点を基準として,翼の前縁から圧力面側に10 mmオフセットさせた位置に設置した場合をカルマン渦が翼の前縁に流入するものとして実験を行いました.
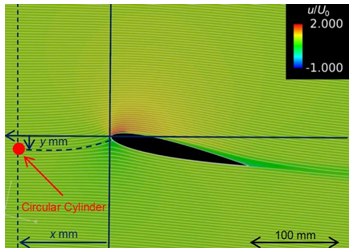
Fig. 2 Time-averaged streamlines and main velocity around airfoil computed by LES
2.3.数値流体解析および空力音響解析
本研究では,対象とする流れが低マッハ数であることから非圧縮のLarge Eddy Simulation(LES)により流体解析を行い,その結果を用いて音響解析を行う分離解法により翼周りの流れと発生する空力騒音のシミュレーションを行いました.流体解析にはFrontFlow/blue(FFB)を使用しました.FFBはフィルター平均されたNavier-Stokes方程式を時間方向にCrank-Nicolson法(2次精度)で離散化し,空間はガラーキン有限要素法(2次精度)により離散化しています.LES解析のSub-Grid Scale(SGS)のモデル化にはDynamic Smagorinsky Modelを用いています.図3に示す解析格子は6面体で作成しており,粘性長さスケールで無次元化した翼近傍の格子解像度はΔx+=20,Δy+=2,Δz+=20となっています.解析領域のスパン方向の長さは翼弦長の5%に設定し,スパン方向には周期境界条件を設定しました.また,円柱周りと翼周りの格子は独立に作成しており,オーバーセット法により接続しています.このオーバーセットによる数値的な振動が発生することを避けるために低マッハ数近似を用いています.要素数は翼部(Grid for Airfoil)が約2800万,円柱部(Grid for Cylinder)が約1500万の合計4300万要素です.
一方,音響解析には,コンパクトな物体がある場合のLighthill方程式の理論解であるCurleの式とFrontFlow/blue-Acoustics(FFB-A)を使用しました.FFB-Aは,Lighthill音源(Lighthillの応力テンソル)の内,運動量の変化量のみを音源として,周波数空間に変換されたLighthill方程式(ヘルムホルツ方程式)をガラーキン有限要素法により離散化して音場を求めます.一般にヘルムホルツ方程式の数値解析では収束性が問題となるため,FFB-Aでは収束性が高いマトリックスソルバーであるIDR法を用いています.本研究では,LES解析により求めた物体(円柱および翼)の流体力変動を用いてCurleの式により空力騒音スペクトルを求めるのとともに,FFBにより計算された瞬時の流れ場(速度)からLighthillの応力テンソルを求め,フーリエ変換したものをFFB-Aに入力し,各周波数における音響解析を実施しました.Curleの式により,円柱から発生するエオルス音など2重極音源が卓越するケースに対して,流体力から簡単に音を求めることができますが,フリースペースのグリーン関数(音場の基本解)を用いているため,翼の後縁から発生する音(後縁騒音)など,物体表面における音の散乱が問題になる場合は適用できません.また,発生する音の指向性を議論することはできません.一方,FFB-Aによる音響解析は,音源データの扱いや計算時間が課題となりますが,音の散乱の影響を取り込むことや,音場の指向性を予測することができます.そのため,本研究ではこれらの二つの方法を併用しました.音響解析の格子は図3のように流体解析格子(Grid for CFD)の外側にさらに拡大した領域をオーバーセットして作成しました.この拡大した領域(Grid for CAA)の要素数は約3300万であり,流体解析部分の格子と合わせて,音響解析の要素数は約7600万要素となります.格子解像度は4 kHzの音波に対して1波長(85 mm)あたり20点(Point per Wave;PPW=20)を満たしています.代表長さは流体解析と同様に翼弦長c=150 mmを1,代表流速は風洞実験と同じく30 m/sを1としており,このときのレイノルズ数は3.0×105,音速340 m/sにおけるマッハ数は0.09となります.
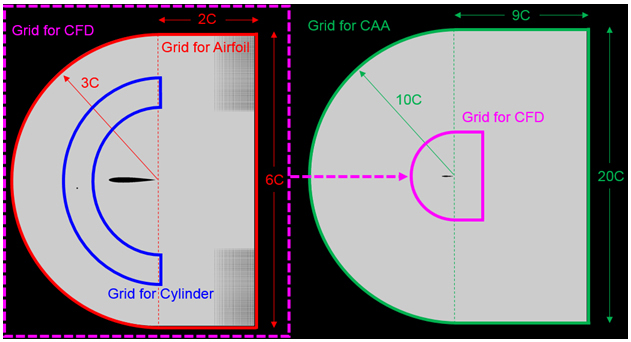
Fig. 3 Computational grids for CFD (left) and CAA (right)
3.結果および考察
3.1.壁面静圧分布と翼騒音スペクトル
直径6 mmの円柱模型を基準点に設置した場合の,翼面の平均静圧と静圧変動,および発生する音をそれぞれ図4, 図5に示します.図5に示した音の周波数スペクトル(音圧レベル)の予測値は,円柱と翼に作用する流体力(合力)からCurleの式により求めたものです.また,静圧変動の実験値は翼模型の片面にのみセンサが内蔵されているため,翼の迎え角と円柱の設置位置を反転させた状態でも計測を行い,2回の計測結果を合わせることで負圧面・圧力面の結果としています.負圧面の静圧変動を正の値,圧力面の静圧変動を負の値として図示しています.
図4の翼面平均静圧を見ると,乱れがある場合は,最大負圧点からの圧力回復が早く,バイパス遷移を起こしていることが確認されますが,乱れの影響は前縁部に限られ,翼全体の流れを大きく変えてはいないといえます.負圧面の境界層がバイパス遷移を起こしていることは,乱れがない場合には,x/c=0.1付近に現れていた,短いはく離泡を伴った遷移に見られる静圧変動のピークが,乱れがある場合には現れていないことからも確認されます.実験結果と流体解析結果は定性的同じ傾向を示しており,本数値解析により現象(風洞実験)が再現されているといえます.図5に示した音のスペクトルでは無次元周波数Stc=5.0付近にピークを見られますが,円柱のエオルス音によるピークです.円柱の後流の渦が流入することで,発生する音が広帯域で増大し,単独の円柱から発生するエオルス音や単独の翼から発生する音よりもはるかに大きくなっています.Curleの式による予測結果は,渦が流入することにより音が顕著に増大するStc<10の周波数帯域においては実験結果を良く再現しています.これらの結果から,単一スケールの変動を持つカルマン渦を流入させても,前縁から徐々に散逸する過程で渦が変形し,それより広帯域で翼騒音が増大すると考えられます.
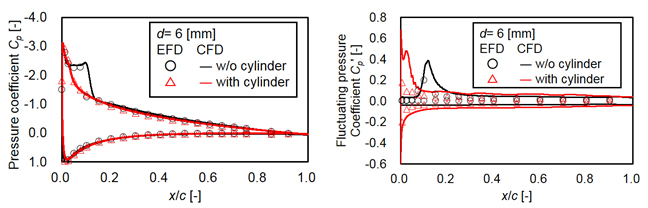
Fig. 4 Mean (left) and fluctuating (right) pressure distributions on airfoil surface
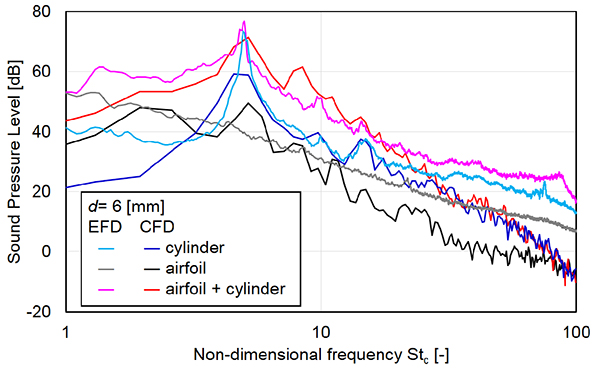
Fig. 5 Frequency spectra of sound radiated from airfoil and/or cylinder
3.2.渦が流入するときの翼周りの流れと音場
図6に瞬時の主流速度uと翼面静圧(Cp)のコンターと∇2p=2000の等値面を可視化した結果を示します.この図から,円柱がない場合は翼面に乱流境界層が発達している様子が現れています.一方,円柱が設置されるとカルマン渦が流入し,淀み点で翼と干渉し,流入した渦が翼面に沿って圧力面と負圧面に分かれる様子が現れています.また,翼との干渉前ではカルマン渦特有の周期的な渦の構造が現れていますが,干渉後は渦が変形し,特に淀み点から負圧面に沿って流れる渦は大きく引き伸ばされている様子が見られます.この際に翼面静圧は淀み点(最大圧力点)から最大負圧点を経由して圧力回復をしています.その後は乱流境界層が発達し,前縁以外では渦との干渉の有無による明確な差異がありません.したがって,淀み点で翼と干渉した渦は,翼の前縁近くの,圧力が急変する部分で大きく変形し,これが翼から発生する音を増大させることが明らかになりました.つまり,流入した渦が翼の淀み点から負圧面にかけての翼まわりの流れの加速により引き延ばされ,その過程で大きな音が発生していることがわかりました.
最後,カルマン渦のピーク周波数Stc=5.0おける,翼と円柱から音が伝播する様子を図7に示します.翼と渦が干渉しない場合は,翼の後縁から音が発生しています.一方,翼と渦が干渉する場合は翼の前縁からも音が発生しています.この結果は,前述した渦が翼の前縁で引き延ばされたために大きな音が発生するということを裏付けているものであると考えられます.

Fig. 6 Static pressure and vertical structures with (right) and without (left) cylinder
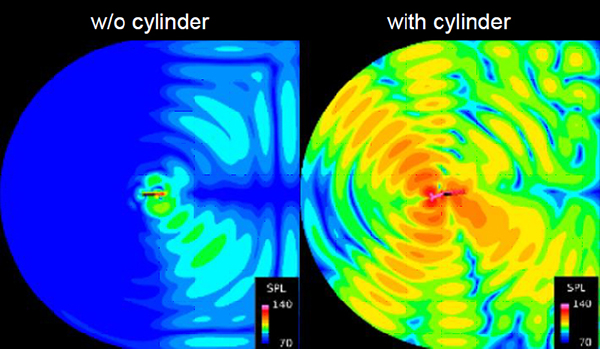
Fig. 7 Sound-pressure level with (right) and without (left) cylinder
4.まとめ
本研究では,2次元形状の対称翼NACA0012(翼弦長150 mm,翼幅長500 mm)の上流側に円柱(直径6 mm)を設置し,円柱から放出されるカルマン渦を翼と干渉させる風洞実験,LESによる数値流体解析および空力音響解析を行いました.
その結果,淀み点で翼と渦が干渉すると広帯域の翼騒音の増大に影響することがわかりました.このとき,翼前縁の静圧変動は負圧面・圧力面ともに増大し,淀み点から負圧面での流れの加速域において流入した渦が引き延ばされていることがわかりました.したがって,干渉した渦が翼の前縁での速度の変化により変形することで翼から発生する音が大幅に大きくなることが明らかになりました.
謝辞
豊橋技術科学大学機械工学系の飯田明由教授には音響解析の実施に際して多大なご助言を頂きました.ここに深く感謝の意を表します.

