油膜貼り付きによる圧縮機弁の開き遅れ挙動のシミュレーション
 吉住文太 豊田中央研究所 |
 近藤靖裕 豊田中央研究所 |
 諸井隆宏 豊田自動織機 |
 玉野真司 名古屋工業大学 |
 森西洋平 名古屋工業大学 |
|
Fumitaka YOSHIZUMI*1, Yasuhiro KONDOH*1, Takahiro MOROI*2, *1Toyota Central R&D Labs., Inc., System & Electronics Engineering Dept. I, 41-1, Yokomichi, Nagakute, Aichi, 480-1192 Japan |
||
1. はじめに
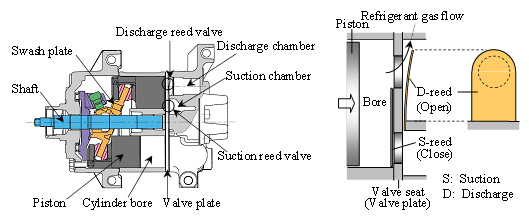
圧縮機(1)の吐出機構として多用されるリード弁は,薄板状のリード(弁体)と弁座から構成され,弁上下流の差圧に応じてリードが弾性変形して開閉する自動弁である(図1).リード弁では,差圧変化に対する開き遅れが問題となることがある.開き遅れは,主として,リードと弁座の間に形成される潤滑油の油膜の貼り付き力,すなわち油膜の「負のスクイズ作用」(二面が離れる際のスクイズ作用)に起因する.負のスクイズ作用では,二面が近付く「正のスクイズ作用」と異なり,油膜内にキャビテーションが発生し得る.今回の対象である弁の貼り付きの挙動でも,油膜の可視化実験において開弁前にキャビテーションの発生が観察された(2).従って,キャビテーションの模擬が,実験の開弁挙動を再現する上での要点となる.
 |
|
| (a) 容積型圧縮機 | (b) 吐出用リード弁 |
図1 容積型圧縮機と吐出用リード弁
油膜のキャビテーションモデルとしては,従来,油膜圧力の下限値を設定するモデル(最低でも真空圧付近を設定)がよく用いられ,弁の貼り付きや二平板間の負のスクイズ作用についても計算例(3)-(11)がある.これに対し,真空圧以下の絶対負圧域(液体内張力)(12)を含む油膜圧力を表現するモデルとして,少数ながら,キャビテーション気泡の成長を直接模擬した例(13)-(15)がある.一方,スクイズ膜の実験(16)(17)でも,負のスクイズ作用によりキャビテーション気泡が急成長する前の油膜圧力として,絶対負圧が計測されている.このため,キャビテーションが観察された弁の貼り付き挙動でも,油膜圧力が絶対負圧域まで低下することが予想され,その計算には気泡成長を直接模擬するモデルが必要と考えられた.
そこで,著者らは,気泡の成長を直接模擬するキャビテーションモデル(以下,「動的キャビテーションモデル」とよぶ),および開弁時の油膜吹き飛び(油膜破壊)モデルを組み込んだ弁の開き遅れ計算モデルを提案した(18).そして,これまで計算との比較例がほとんどなかった実験における貼り付き力(すなわち開き遅れ時間),および油膜挙動を再現することを試みた(19).本稿では,その概要について紹介する.
2.計算モデル
図2に示す弁単体の実験(2)を対象として,リード変形,ガス流れ,油膜の3フェーズをそれぞれモデル化して連成させた.このうち,リード変形を有限要素法のシェル要素で表現し,ガス流れを熱力学モデル(集中定数モデル)で表現した.
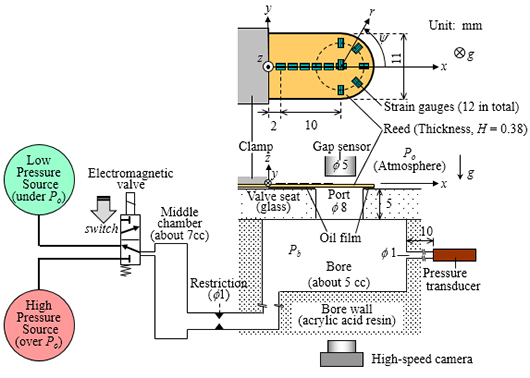
図2 弁の開き遅れ挙動計測装置
2.1 動的キャビテーションモデル
油膜のモデル化に関して,過去の検討結果(13)-(15)も踏まえながら,気泡成長を直接模擬する「動的キャビテーションモデル」を考案した.「動的キャビテーションモデル」を用いた油膜のモデルを図3に示す.図に示すように,気泡形状を球形に仮定し,気泡成長の方程式と油膜の基礎方程式であるレイノルズ方程式(有限体積法で離散化)を連成させて,油膜圧力を求める.ただし,レイノルズ方程式は気泡成長の影響を考慮して以下のように修正される.
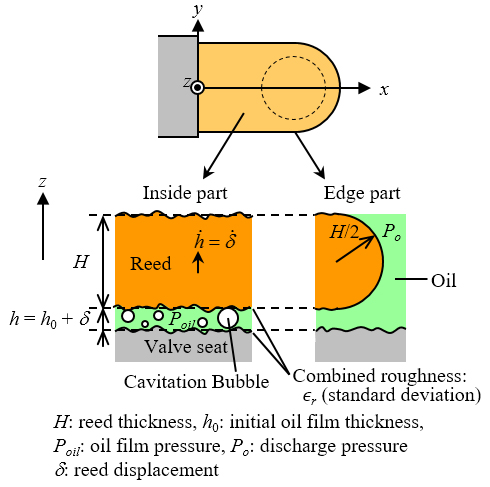
図3 「動的キャビテーションモデル」を用いた油膜モデル(18)
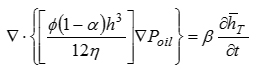 |
(1) |
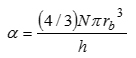 |
(2) |
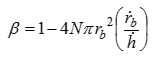 |
(3) |
気泡半径の成長方程式は,オーダー比較により慣性項を無視して,以下の式(4)で表される.この式(4)のほか,油中溶存ガスの気泡内への拡散の方程式,および気泡内ガス圧力(Pg )の方程式を連立して気泡成長を模擬する.
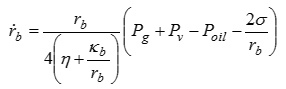 |
(4) |
ここで,式(1)~(4)において,∇はナブラ記号,hは油膜厚さ,hTは粗さを考慮した局所油膜厚さ,Nは油膜を介した接触面の単位面積当たりの気泡個数(不変とする),Pgは気泡内ガス圧力,Poilは油膜圧力,Pvは油の飽和蒸気圧,rbは気泡半径,α は油膜のボイド率,β は油膜体積変化の液体分率,η は油の粘度,κbは気泡の表面膨張粘性係数,ϕ は粗さを考慮した油膜の圧力流量係数である.気泡は,油膜圧力がPcav onset(本稿では,0 MPa-absと仮定)まで低下すると成長するものとする.このPcav onsetのほか,油中の溶存ガス量(体積比で一般に数%~10%程度)を参考にrbの初期値(1µmオーダー)とN(1×1010 m-2)を仮定して与える.
「動的キャビテーションモデル」の特徴と機能を以下にまとめる.
・指標β による気泡成長の影響の定量化:気泡成長が負のスクイズ作用を阻害する程度を表す指標β を新たに定義する.すなわち,β = 1は油膜(隙間)の体積変化がすべて油の流出入で占められている状態,β = 0が油膜(隙間)の体積変化がすべて気泡成長で占められスクイズ作用による圧力低下が阻害されている状態に対応する.
・気泡の表面膨張粘性係数κbの考慮:以下の知見を基にκbを考慮する.まず,直径1 mm以下の気泡の膨張ではκbの影響が大きいことが指摘されている(20).また,計算で得られる絶対負圧の持続時間は κb に依存し,κbを考慮すると実験の貼り付き時間と同じ10 msオーダー(13)であり,考慮しないとµsオーダー(14)である.κbの値は,過去の検討例(13)(20)を基に設定する.なお,本稿の弁挙動計算は,κbを考慮しないと発散する.
・絶対負圧(張力)を生じる油膜とリード変形の連成:気泡成長と連成させた油膜圧力を,油膜厚さhを介してさらにリード変形と連成させる.絶対負圧域を含む油膜の最低圧は,この連成計算の中で結果的に求められる.なお,Pcav onset > 0 MPa-abs(例えば,Pcav onset = 0.05 MPa-abs)に仮定しても,気泡半径rbの初期値やκb次第で油膜に絶対負圧が生じる.
2.2 油膜吹き飛びモデル
弁は,貼り付きののち,最終的にはポート周りの油膜が吹き飛んで開弁に至る.そこで,開弁時の油膜の吹き飛びを表現する以下のモデルを導入する.まず,有限体積法のセルごとに,ポート周り半径方向の流量の時間積分値を求める.その積分値を閾値と比較することで吹き飛びの発生を判定する.閾値は,実験の可視化画像を基に,初期状態でポート縁に付着した油の体積を推定して与える.
3. 実験との比較
3.1 開き遅れ挙動の比較
ポート中心上の弁変位δpとボア(圧縮室)圧力Pbの時間変化を図4に示す.実験(図中「experiment」)では,ボア圧力Pbが吐出圧Poに到達(この時点をt = 0 msとする)した後もリードが弁座に貼り付いて17 msの開き遅れ時間が生じ,その間Pbが上昇を続ける(過圧縮に相当).
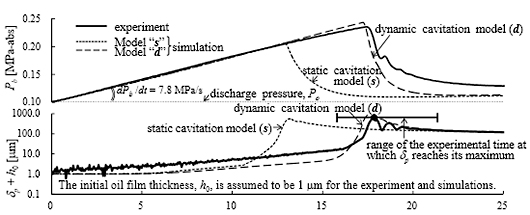
図4 弁変位(δp)とボア圧力(Pb)の時間変化
実験の開き遅れ時間は,rbの初期値やκbの調節が必要であるが,「動的キャビテーションモデル」を用いた計算で再現できる(図中「Model “d”」).図には,油膜圧力の下限値(Pcav)を設定する従来のキャビテーションモデル(以下,「従来モデル」)を用いて,Pcav = 0 MPa-abs(油の蒸気圧付近)としたときの結果も示している(図中「Model “s”」).従来モデルでは実験より早く開弁し,開き遅れ時間を再現できない.両モデルの開き遅れ時間の違いは,4節に示すように,油膜の最低圧力の違いに起因している.
3.2 油膜挙動の比較
開弁(油膜の吹き飛び)直前における実験の可視化画像と「動的キャビテーションモデル」によるボイド率を比較して図5に示す.キャビテーションの発生状況について,実験では,ポート周りシール部の先端側で発生したのち,シール上を先端側から根本側に移動して(先端側では消滅),根本側接触面全体に拡がる.計算でも,ボイド率の高い領域が同様の挙動を示しており,キャビテーションの発生と移動のパターンを再現している.
 |
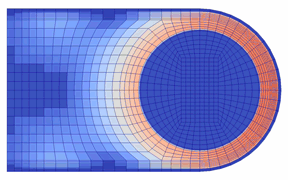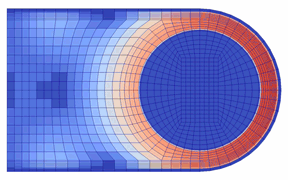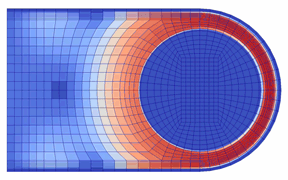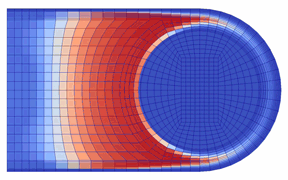 |
図5 キャビテーション発生状況の比較
(左:可視化画像,右:計算によるボイド率,ともに油膜吹き飛び開始直前1.4 ms間)
その後の油膜の吹き飛び(開弁)状況について,実験の可視化画像と計算を比較して図6に示す.油膜の吹き飛び挙動についても,時間ステップごとの吹き飛び領域が実験と計算でほぼ対応している.
 |
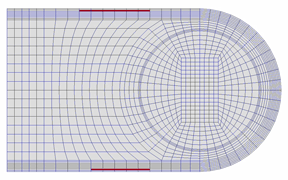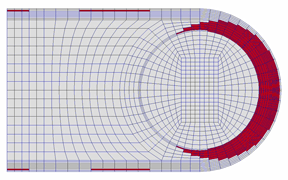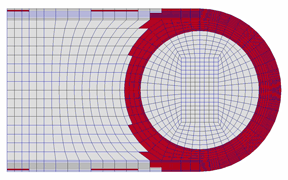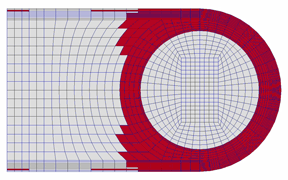 |
図6 開弁時の油膜の吹き飛び状況の比較
[左:可視化画像,右:計算による吹き飛び領域(赤色), ともに0.6 ms間]
4. 計算における油膜諸量の考察
「動的キャビテーションモデル」の計算で得られた油膜諸量(Poil,α,β )を図7に示す.「動的キャビテーションモデル」では,ボア圧力の上昇とともに油膜圧力Poilが絶対負圧(張力)まで低下する領域が拡がる.一方の従来モデルでは,Poilの下限値がPcav = 0 MPa-absに制限されPoil = Pcavの領域が拡がる(19).この最低圧力の違いが貼り付き力の違いとなり,両モデルの開き遅れ時間に差異(図4)をもたらしている.これより,開き遅れ時間を定量的に再現するには,油膜の絶対負圧を考慮できるキャビテーションモデルが必要といえる.
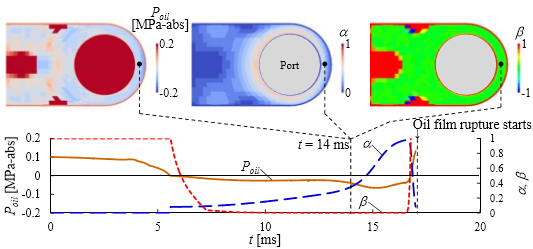
図7 「動的キャビテーションモデル」の計算で得られる油膜諸量
(Poil:油膜圧力,α:油膜のボイド率,β:油膜体積変化の液体分率)
油膜体積変化の液体分率β に着目すると,キャビテーションの発生が油膜圧力分布に及ぼす影響を考察できる.シール先端を含め,キャビテーションが生じている領域(Poil < Pcav onset = 0 MPa-abs)の大部分でβ ≒ 0となっている.β ≒ 0の領域では油膜(隙間)の体積変化がほとんど気泡成長で占められている.すなわち,キャビテーションにより油膜の圧力低下が阻害され,絶対負圧(張力)の大きさが制限されていることが分かる.
5. おわりに
本稿で紹介したシミュレーション計算は,気泡に関する入力諸元(初期径,数密度,表面膨張粘性係数)の決め方に課題があるが,実験におけるパラメータ(リードと弁座間の接触面積,開弁前のボア圧力上昇速度等)の影響を概ね再現する(19)(21).本計算により,各パラメータと開き遅れ時間の関係,およびそのメカニズムの理解が可能となる.
文 献
| (1) | 株式会社 豊田自動織機,“コンプレッサーの種類とその構造 片側斜板式(可変容量型)”, https://www.toyota-shokki.co.jp/about_us/business/automobile/compressor/kind_4/index.html (参照日2016年11月2日). |
| (2) | 吉住文太,近藤靖裕,吉田一徳,諸井隆宏,玉野真司,森西洋平,“圧縮機の冷媒ガス吐出用リード弁における開き遅れ現象(開弁過程における油膜挙動の可視化と弁変形計測)”,日本機械学会論文集C 編, Vol. 78, No. 795 (2012), pp. 3787-3802. |
| (3) | Bauer, F., “The Influence of Liquids on Compressor Valves”, Proceedings of the 1990 International Compressor Engineering Conference at Purdue (1990), pp. 647-653. |
| (4) | Khalifa, H. E., and Liu, X., “Analysis of Stiction Effect on the Dynamics of Compressor Suction Valve”, Proceedings of the 1998 International Compressor Engineering Conference at Purdue (1998), pp. 87-92. |
| (5) | Bukac, H., “Understanding Valve Dynamics”, Sixteenth International Compressor Engineering Conference at Purdue (2002), C15-3. |
| (6) | Courtois, S., Arnoult, E., Wagstaff, P., and Gavric, L., “On Finite Element Modeling of Valve Dynamics: Impacts, Oil Stiction, Gas Flow, …”, Sixteenth International Compressor Engineering Conference at Purdue (2002), C13-2. |
| (7) | Hays, D. F., and Feiten, J. B., “Cavitation between Moving Parallel Plates”, In Proceedings of the Symposium on Cavitation in Real Liquids (GM Research Labs, Warren, Michigan; Elsevier Publishing Co., New York) (1962),pp. 122-138. |
| (8) | Haber, S., and Etsion, I., “Analysis of an Oscillatory Oil Squeeze Film Containing a Central Gas Bubble”, ASLE Transactions, Vol. 28, No. 2 (1985), pp. 253-260. |
| (9) | Boedo, S., and Booker, J. F., “Cavitation in Normal Separation of Square and Circular Plates”, Transactions of the ASME, Journal of Tribology, Vol. 117, No. 3 (1995), pp. 403-410. |
| (10) | Optasanu, V., and Bonneau, D., “Finite Element Mass-Conserving Cavitation Algorithm in Pure Squeeze Motion. Validation/Application to a Connecting-Rod Small End Bearing”, Transactions of the ASME, Journal of Tribology, Vol. 122, No. 1 (2000), pp. 162-169. |
| (11) | Sun, D. C., Wang, W., Zhang, Z., Chen, X., and Sun, M., “Theory of Cavitation in an Oscillatory Oil Squeeze Film”, Tribology Transactions, Vol. 51, Issue 3 (2008), pp. 332-340. |
| (12) | Temperley,H. N. V., “The Tensile Strength of Liquids”, In Cavitation and Related Phenomena in Lubrication, Proceedings of the 1st Leeds-Lyon Symposium on Tribology, University of Leeds, Leeds, UK (Mechanical Engineering Publications Ltd, London, UK) (1974), pp. 11-13. |
| (13) | Natsumeda, S., and Someya, T., “The Effect of the Surface Dilational Viscosity to the Negative Pressure in the Oil Film of Journal Bearing”, Proceedings of the Japan International Tribology Conference (1990), pp. 1617-1622. |
| (14) | Geike, T., and Popov, V. L., “A Bubble Dynamics Based Approach to the Simulation of Cavitation in Lubricated Contacts”, Transactions of the ASME, Journal of Tribology, Vol. 131, No. 1 (2009), 011704. |
| (15) | Gehannin, J., Arghir, M., and Bonneau, O., “Evaluation of Rayleigh-Plesset Equation Based Cavitation Models for Squeeze Film Dampers”, Transactions of the ASME, Journal of Tribology, Vol. 131, No. 2 (2009), 024501. |
| (16) | 黒田成昭,堀幸夫,“スクイズフィルムの研究-負のスクイズにおけるキャビテーションと流体内張力について-”,潤滑, Vol. 23, No. 6 (1978), pp. 436-442. |
| (17) | Sun, M., Zhang, Z., Chen, X., Wang, W., Meng, K., and Sun, D. C., “Experimental Study of Cavitation in an Oscillatory Oil Squeeze Film”, Tribology Transactions, Vol. 51, Issue 3 (2008), pp. 341-350. |
| (18) | 吉住文太,近藤靖裕,諸井隆宏,玉野真司,森西洋平,“圧縮機の吐出用リード弁における開き遅れ挙動の計算(弁変形-ガス流れ-油膜流れ連成計算のためのモデル化)”,日本機械学会論文集B 編,Vol. 79, No. 806 (2013), pp. 1985-2002,およびVol. 79, No. 808 (2013), p. 2885. |
| (19) | 吉住文太,近藤靖裕,諸井隆宏,玉野真司,森西洋平,“圧縮機の吐出用リード弁における開き遅れ挙動の計算(弁変形-ガス流れ-油膜流れ連成挙動と開弁メカニズム)”,日本機械学会論文集B編, Vol. 79, No. 806 (2013), pp. 2003-2018. |
| (20) | 井田富夫,杉谷恒也,“圧力変化を受ける油中の気ほうの運動:第1報,単一気ほうの実験解析”,日本機械学会論文集B編, Vol. 45, No. 399 (1979), pp. 1650-1658. |
| (21) | 吉住文太,諸井隆宏,玉野真司,森西洋平,“圧縮機の吐出用リード弁の開き遅れ挙動における作動条件と弁剛性の影響”,日本機械学会論文集, Vol. 80, No. 812 (2014), FE0091, pp. 1-15. |

