インバータロータリ圧縮機の吸込配管系における過給効果の予測手法
1. はじめに
空調機では、幅広い運転範囲での省エネが求められており,モータ回転数をインバータで可変するロータリ圧縮機が用いられている.圧縮機を設計する上で,冷媒の循環量が大きい高負荷条件が重要であるが,この条件では吸込配管系の気柱共鳴により,特定の回転数で循環量が増大する過給効果が知られている(1)(2).
著者らは過給を有効に活用するために,二段圧縮機を含めたインバータロータリ圧縮機の寸法や回転数等の設計因子が体積効率に及ぼす影響を実験と解析で考察し,簡便かつ高精度に予測する手法を提案した.
2. 実 験
実験は,二種類の冷媒を用いた単段圧縮機3種類,二段圧縮機1種類を対象とした.これらはルームエアコン用で,定格出力が1 kW級である.単段圧縮機の吸込配管系を,図1に示す.各圧縮機の理論吸込体積Vは8.7~22.7 cm3である.次に二段圧縮機の構造を,図2に示す.二段圧縮機は,一段目シリンダを下部に,二段目を上部に配置し,一段目吐出室を介して両者を連通した構造である.ただし一段目の吸込配管系は,単段圧縮機と同じ構造である.
次に各圧縮機の性能を,ガス流量計測式カロリーメータで測定した.冷媒の循環量Gと圧縮機モータ入力W,吸込sと中間mでの圧力Pと温度T,および吐出圧力Pdを測定した(図2).実験条件は,低外気温度での暖房運転に合わせ,モータ回転数fはインバータ設定した.
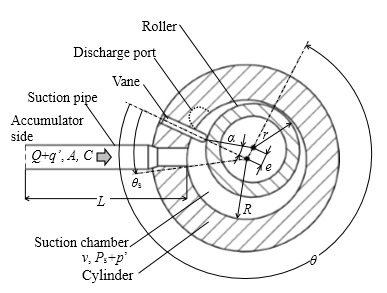
図1 吸込配管系の構造
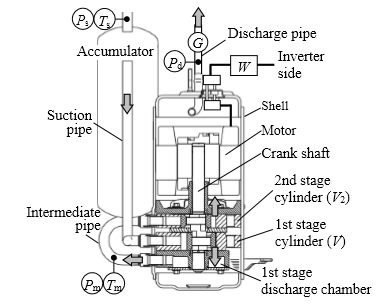
図2 実験装置(二段圧縮機)
体積効率ηvの結果を,図3に示す.単段圧縮機S1では,回転数fが55 s-1から増大するに伴いηvが指数関数的に増大した.共振回転数fnは157 s-1で,共振点nの体積効率ηv,nが基準特性ηv,0に対して14%増加した.同様に,単段圧縮機S2や二段圧縮機Tでも過給効果が確認された.過給によるηv,nの増加量が12~14%でほぼ一致していることから,次章で支配因子を適切に選定してηvの増加量を整理することとした.
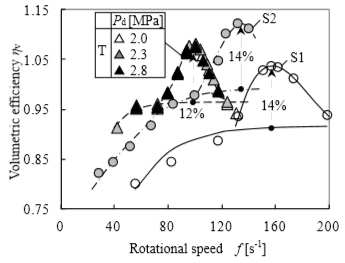
図3 体積効率の実験結果
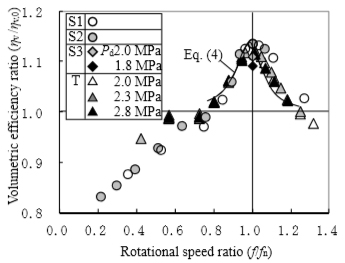
図4 体積効率の無次元整理
3. 無次元整理
支配因子を特定するため,冷媒流れを一次元非圧縮性流体でモデル化した(図1).体積流量を(Q+q’),吸込室の圧力を(Ps+p’)で表す.ここで大文字は過給に依存しない定常成分,添え字(’)は変動成分である.音響理論を適用すると,吸込配管における運動量の保存則は,
| (1) |
となる.ここでtは時間,μは減衰抵抗係数,Aは配管の流路断面積,ρは吸込密度である.さらに吸込室での等エントロピ変を仮定して整理すると,
| (2) |
を得る.さらに式(2)の吸込体積vをフーリエ級数展開すれば厳密解が得られるが,取り扱いがやや複雑となる.そのため,過給特性を再現しながら式(2)を線形化することとした.ここで共振現象はクランク角度θ=π周辺で最大となることが知られており,θ=π周辺のvと(dv/dθ)を次式で近似した.
| (3) |
式(3)を式(2)に代入して整理すると,強制振動における線形方程式を得る.その定常解q’は直ちに求まり,過給に伴う体積流量の増加量を次式で表すことができる.ここでaは比例定数,fnは共振回転数,ζは減衰比である.
| (4) |
| (5) |
2章の実験データから共振回転数fnと基準特性ηv,0を求め,体積効率ηvを無次元整理した.効率比(ηv/ηv,0)と回転数比(f/fn)の関係を,図4に示す.図4より,(f/fn)が約0.8~1.2の範囲で,圧縮機寸法や冷媒種類等に関係なく,過給効果(ηv/ηv,0)を(f/fn)で整理できることが分かった.なお,3章では,吸込室の圧力変動が最大となるクランク角度θ=π周辺のみを近似した.そのため過給の位相すなわち共振回転数fnについては,次章で定式化することとした.
4. 共振回転数の予測式
4・1 基礎式
共振における吸込室の圧力変動p’の物理モデルを,図5に示す.p’が周期関数であると仮定し,クランク角度θ,回転数f,時間tの関係を示した.ここで吸込体積vに起因する圧力波を,矩形波-Δpとして単純にモデル化した.
| (a) t =0, θ=θs: | 正の圧力変動+p’(θs)がローラにより同位相で反射され,後進波がアキュムレータ側の開放端へ伝播する. |
| (b) t =L/C, θ=θs+ 2πf L/C : | 後進波が粘性により減衰して開放端に至り,逆位相で反射され負の進行波が伝播する.ここで,開放端の圧力変動を0とした. |
| (c) t =2L/C,θ=θs+ 4πf L/C : | 減衰した進行波が,吸込室端に至る. |
| (d) t =2L/C,θ=θs+ 4πf L/C : | (c)と同時に,進行波がローラやシリンダにより同位相で反射され,負の反射波が生じる.一方,吸込体積vの時間変化により,負の圧力波-Δpが新たに供給される.反射波と圧力波を合わせた負の合成波が,伝播する. |
| (e) t =3L/C,θ=θs+ 6πf L/C : | 減衰した負の後進波が開放端で反射され,正の前進波が伝播する. |
| (f) t =4L/C,θ=θs: | 減衰した前進波が吸込室端に至り,(a)の状態が形成される. |
ここで粘性減衰がある程度大きく,Δpが反射波よりも十分大きければ,p’(θs) ≈Δpと近似でき,さらにΔp は音響理論における運動量の保存則から(dv/dθ)に比例する.すなわちΔpが,(dv/dθ)が極大となるθ=πで供給されれば,p’(θs)が極大すなわち共振状態となる.
(dv/dθ)は幾何学的にθ=πで極大だから,図5(d)におけるθ=πが共振条件と考えられる.したがってπ=θs+4πfn L/Cの関係が成り立ち,これを整理すると,
| (6) |
の基礎式を得る.式(6)は, Helmholtzの式(1) fn=C/(4L)に圧縮機寸法θsの影響を補正したものである.
fnの実験meaと式(6)の計算calの関係を,図6に示す.図より,式(6)は実験に対して1~18%低く,fnの増大に伴い誤差が小さくなることが分かった.
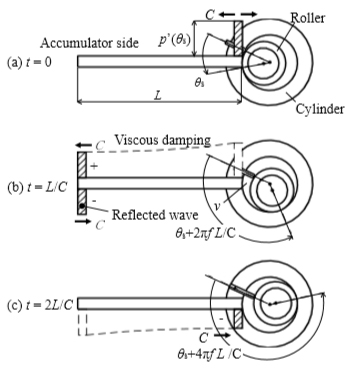
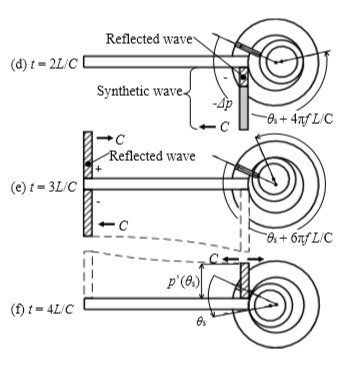
図5 共振回転数fn付近の圧力変動のモデル
4・2 吸込室寸法の補正
式(6)の誤差がfnの低下に伴い拡大する要因として,圧力変動を矩形波でモデル化した影響が考えられる.波長と吸込室の寸法の影響を考慮して,補正を試みた.クランク角度0~θsの吸込室の代表寸法として,シリンダ半径Rとθsの円弧(Rθs)をとる.圧力変動の波長は配管長Lのオーダであるから,波長に対する吸込室の寸法を表すパラメータは(Rθs/L)となる.(Rθs/L)をパラメータとした補正係数βを定義し,fnの基礎式(6)を次式のように補正した.
| (7) |
式(7)は,βが0ならばθsの影響を省略したHelmholtzの式に,βが1ならば式(6)に一致することを想定している.式(7)を変形して,実験値fn,meaから求めたβを,図7に示す.
図より,実験結果からもβが0~1の範囲で変化することを確認できたので,(Rθs/L)→0でβ→0,(Rθs/L)→1でβ→1となるようにβを双曲関数で近似し,最小自乗法で係数を計算した結果,以下の実験式を得た.
| (8) |
以上より,圧縮機の寸法R,L,θsと,冷媒種類と運転条件を代表する音速Cから,過給の共振回転数fnを予測する式を得た.式(7)の予測誤差は,本実験範囲において-3~+1%であり,圧縮機設計に供しうる精度と考える.
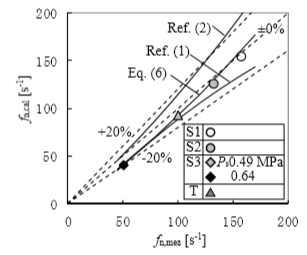
図6 共振周波数fnの実験と計算の比較
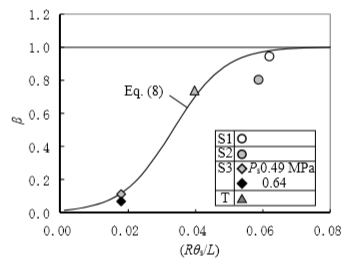
図7 寸法因子(Rθs/L)と補正係数βの関係
5. おわりに
二段圧縮機を含めたインバータロータリ圧縮機の過給効果を予測するため,圧縮機寸法と冷媒種類,運転条件が異なる実験を行い,過給に伴う体積効率の増加量と共振回転数を,それぞれ単純な理論解析に基づきデータを整理した結果,以下の結論を得た.
| (1) | 単段圧縮機・二段圧縮機の一段目に関して,過給による体積効率の増加量(ηv/ηv,0)を,回転数比(f/fn)をパラメータとした相関式で表した |
| (2) | 共振回転数fnが高い場合,fnを,配管長Lと冷媒の音速Cに加え,吸込終了時のクランク角度θsを考慮した基礎式(6)で表した. |
| (3) | fnが低い場合,波長に対する吸込室寸法の影響を補正する係数βを定義し,実験式(7)(8)を得た. |
文 献
| (1) | 伊藤茂, 大谷巌, 橘久, 山本嘉巳, 容積形圧縮機 (1970), pp.82-85, 産業図書. |
| (2) | 伊藤毅, 音響工学原論, Vol.1 (1955), pp.171-175, コロナ社. |




