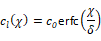上昇気泡からの高シュミット数条件下における物質輸送の数値解析手法の開発

足立 理人 大阪大学 (現 三菱電機(株))	大森 健史 大阪大学	梶島 岳夫 大阪大学

1.　はじめに

　液中の上昇気泡から気体成分を溶解させる操作は，多くの工業的分野において用いられ，例えば，水質浄化装置，反応装置や二酸化炭素の海洋隔離装置などの性能を決定づける．これらの装置において高い気体溶解効率を達成するためには，多数の気泡の相互干渉によって生じる複雑な流れおよび物質輸送に対する深い理解が必要となる．数値計算による解析は領域全体で流れ場および濃度場の詳細な情報の取得を可能とし，種々の因子の効果を個別に調査可能であるため，そのような理解を助ける手段として大変有効であるといえる．多くの工業プロセスにおいて用いられる酸素や二酸化炭素といった難溶性気体では，気体の液相側における拡散係数と液体の動粘性係数の比であるシュミット数が大きく，液相側界面近傍に形成される濃度境界層は速度境界層と比較して薄くなる．数値解析においては，気体成分の移流に加えて溶解および薄い濃度境界層内での拡散過程を正しく再現することが要請され，従来の計算手法（例えばFigueroa-Espinoza and Legendre, 2010およびBothe and Fleckenstein, 2013）では，計算コストが膨大になることが問題であった．

　 本研究では，高シュミット数条件下における濃度境界層の相似性に着目し，液相側界面近傍の気相成分の物質量を保存するように濃度境界層を相補誤差関数で「再構成」することにより，濃度境界層厚さが計算セル幅に満たないような場合においても気体成分の溶解・拡散量を精度良く計算できる合理的な手法を提案した．ここでいう「再構成」とは，各計算セルの代表点のみで離散的に定義される濃度からサブグリッドの濃度分布を構成することを指す．本計算手法においては，物質量や運動量の保存性が考慮されている点と単調な相補誤差関数を用いたことにより計算の安定性が損なわれていない点が重要である．

　 なお，本計算手法は任意のVOF（Volume-of-Fluid）法と組み合わせて使用することが可能であり，拡張性が高い点も利点といえる．計算手法の詳細については著者らによる論文（足立ら, 2016）を参照していただくとして，ここでは計算手法の概要と計算精度の検証結果を紹介する．

2.　 計算手法の概要

2・1　基礎方程式
液相および気相は非圧縮ニュートン流体とし，各相における流体の運動は連続の式および運動量保存式にしたがうものとする．また，液相内における気体成分濃度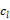は以下の移流拡散方程式にしたがうものとする．

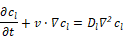( 1 )

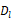は液相内における気体成分の物質拡散係数である．本研究では薄い濃度境界層を伴う物質輸送の解析手法の開発が主眼であり，これとは独立に考慮することができる気体成分の溶解に伴う気相の体積変化については取り上げず，物質量の保存は液相内においてのみ考えることとする．また，液相側の濃度分布の解析に対しては気液界面上で常に飽和濃度であるという境界条件を与える．
気液界面の捕獲にはVOF法を用いる．提案する物質輸送モデルにおいては気液界面位置が幾何学的に一意に定まっている必要があるので，界面の再構成にはmixed Youngs-centered method (Aulisa et al., 2007) を，移流にはsplit Lagrangian-explicit scheme (Gueyffier et al., 1999) (LE法) を採用しており，本研究においては，計算格子は直交等間隔であることを前提としている．

2・2　物質輸送モデル
式(1)の時間発展は，得津ら (2011) と同様に溶解・拡散ステップと移流ステップに分離することによっておこなう．提案する物質輸送モデルは，高シュミット数条件下における境界層近似（Stewart et al., 1970; Bird et al., 2002）に基づいており，各計算セルで切り取られた微小気液界面要素ごとに，要素法線方向に対して境界層近似解と相似な濃度分布を用いて，気体成分の溶解量および気液界面近傍における拡散量を計算する．すなわち，Fig. 1に示すように気液界面付近の計算セルにおいて気相から液相へ向かう界面法線方向の座標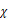をとすると，以下の式のように 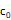を飽和濃度として溶解気体濃度分布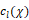を仮定する．

( 2 )

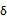ただしおよびは気液界面を有する計算セルごとに定義し，界面法線方向は界面の幾何学的再構成を行う際に与えられる．濃度境界層厚さを表す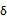は，気液界面付近の液相内への気体成分溶解量と式(2)のに関する積分値が整合するように与える．
気液界面から離れた計算セルにおける気体成分拡散量の計算には標準的な差分法を用いる一方で，気液界面からの気体成分溶解量および気液界面近傍の計算セルにおける気体成分拡散量の計算には式(2)の解析的な微分を用いる．気体成分移流量の計算には，気液界面近傍ではLE法を応用した手法 (得津ら，2011) を，その他の領域では三次精度のMUSCL法を用いる．

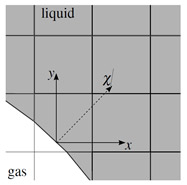
Fig. 1 気液界面要素における局所座標の定義

3.　物質輸送モデルの検証

3・1　二次元静止気泡周囲の物質拡散
　提案手法を二次元静止気泡周囲の物質拡散問題に対して適用した計算の結果を解析解と比較する．計算領域をFig. 2に，計算結果をFig. 3からFig. 4に示す．提案手法による結果が気液界面と計算セルの位置関係に依存しないことを検証するため，静止気泡の中心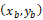は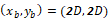， (Case 1)および 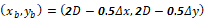(Case 2)の2種類について計算を行った．

　 Fig. 3では，(a)および(b)がCase 1，(c)および(d)がCase 2の場合の計算結果を示しており，解析解を曲線で，溶解気体成分の各計算セルでの積分値を棒グラフで表している．また、同図(a)および(c)では濃度境界層厚さが1セル程度の時間における結果を、(b)および(d)では濃度境界層厚さが3セル程度の時間における結果を示している。同図からわかるように計算結果と解析解は高い精度で一致しており，溶解気体成分が液相内で保存されていることが確認できる．また，(a)および(c)では濃度境界層厚さが1セル程度の時間においても各セルで積分した溶解気体成分が解析解と良好に一致している．

　 Fig. 4は液相内への気体成分総溶解量の時間変化を示している．解析解と計算結果との間の相対誤差はすべての時間において3%以内である．このように，濃度境界層厚さが1セルに満たない条件下においても溶解・拡散量を良好に計算できることが提案手法の利点である．

Fig.2 拡散問題における計算領域

Fig. 3水平方向濃度分布の解析解と提案手法の計算結果の比較

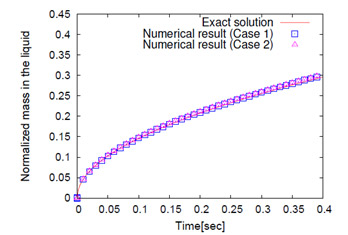
Fig. 4 液相内への気体成分総溶解量の時間変化

3・2　二次元上昇気泡からの物質輸送
　シュミット数100の条件下において，提案手法を二次元上昇気泡周囲の濃度場解析に適用した結果を直接差分計算による高格子解像度の計算結果と比較する．計算条件をTab. 1 に，計算領域をFig. 5に，計算結果をFig. 6からFig. 8に示す．初期気泡径Dに対する格子数を20mとして，m=1から12の間で解像度を変化させた．気泡の終端速度に対するレイノルズ数は各解像度において約29である．

　 Fig. 6は，気泡の上昇速度が一定となった時間0.18sec における溶解気体濃度分布をカラーマップで示している．同図(a)では，(b)および(c)と比較して気泡の後流領域の濃度分布に相違が見られる．この相違はバルク領域における濃度の移流計算に対する解像度不足によって生じている．Fig. 7は，y=5.5mmの気泡後流領域における水平方向の時間0.18secでの濃度分布を示している．同図においてm=2の解像度でバルク部の濃度分布は良好な結果が得られていることから，提案手法では差分ベースの手法に対してはるかに少ない格子分割数で精度の高い解析が可能であることがわかる．

　 Fig. 8は，液相内への気体成分総溶解量の時間変化を示している．縦軸は初期の気泡内に存在する気体量で規格化した溶解気体量である．提案手法を用いた計算における0.11sec以降の平均溶解速度（Fig. 8の実線の傾き）はm=12で予測された平均溶解速度と3%以内の相対誤差で一致している． 計算開始直後にはグラフが上に凸，すなわち溶解速度の大きいことがわかる．気泡上昇の初期に見られるような濃度境界層が薄い状況であっても提案手法は溶解・拡散量を精度良く計算可能である．

Tab. 1 計算条件

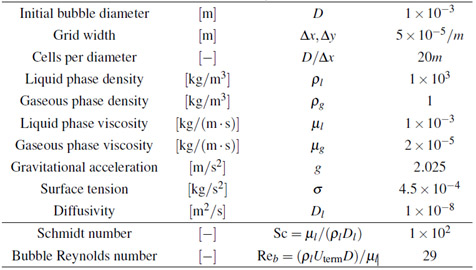
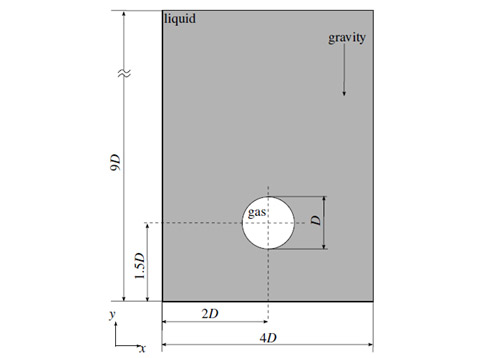
Fig. 5 計算領域と初期気泡形状および配置

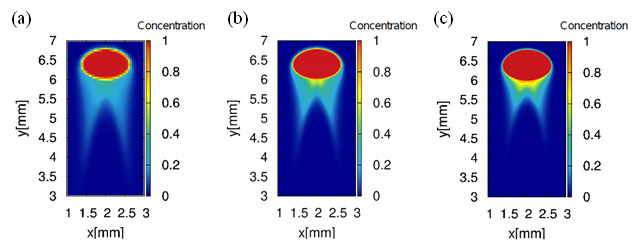
Fig. 6 溶解気体成分の濃度分布 ((a)m=1での提案手法，(b)m=2での提案手法，(c)m=12での従来手法)

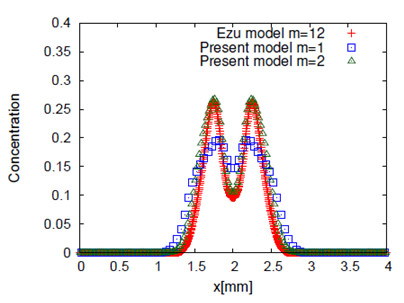
Fig. 7 気泡後流領域における水平方向濃度分布

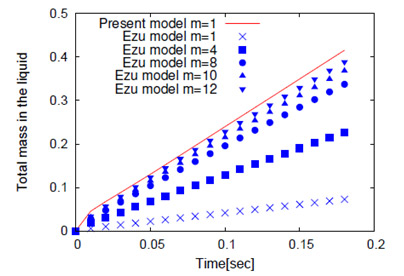
Fig. 8 上昇気泡からの気体成分総溶解量の時間変化

4.　おわりに

　 本記事では，著者らが開発した，高シュミット数条件下における物質輸送の解析手法（足立ら, 2016）について紹介した．本手法により，高シュミット数条件下においても速度場の解析に必要な程度の格子解像度で，流体運動を伴う物質輸送を高精度に解析することが可能である．

　 本計算手法は，濃度境界層の直接差分計算と比較して計算コストを大幅に削減することが可能であり，気泡集団によるマルチスケール性が顕在化するような大規模系における物質輸送の予測への応用が期待される．

文　　　献

足立理人，大森健史，梶島岳夫，上昇気泡からの高シュミット数条件下における物質輸送の数値解析手法の開発，日本機械学会論文集，Vol. 82, No. 839 (2016) .
得津裕太郎, 大森健史, 梶島岳夫, 上昇する気泡周りの流れと物質移動に関する数値シミュレーション, 混相流,Vol. 24, No. 5 (2011), pp. 539-547.
Aboulhasanzadeh, B., Thomas, S., Taeibi-Rahni, M. and Tryggvason, G., Multiscale computations of mass transfer from buoyant bubbles, Chemical Engineering Science Vol. 75 (2012), pp. 456–567.
Aulisa, E., Manservisi, S., Scardovelli, R. and Zaleski, S., Interface reconstruction with least-square fit and split advection in three-dimensional Cartesian geometry, Jounal of Computational Physics, Vol. 225, No. 2 (2007), pp. 2301–2319.
Bird, R., Stewart, W. E. and Lightfoot, E. N., Transport Phenomena, 2nd edition, John Wiley and Sons, Inc (2002).
Bothe, D. and Fleckenstein, S., A Volume-of-Fluid-based method for mass transfer processes at fluid particles, Chemical Engineering Science Vol. 101 (2013), pp. 283–302.
Figueroa-Espinoza, B. and Legendre, D., Mass or heat transfer from spheroidal gas bubbles rising through a stationary liquid, Chemical Engineering Science Vol. 65 (2010), pp 6296 - 6309.
Gueyffier, D., Li, J., Nadim, A., Scardvelli, R. and Zaleski, S., Volume-of-Fluid interface tracking with smoothed surface stress method for three-dimensional flows, Journal of Computational Physics, Vol. 152, No. 2 (1999), pp. 423–456..
Stewart,W. E., Angero, J. B. and Lightfoot, E. N., Forced convection in three-dimensional flows: II. Asymptotic solutions for mobile interfaces, Journal of American Institute of Chemical Engineers, Vol. 16, No. 5 (1970), pp. 771–786.