台風はどちら向きに回転?
まずは見てみよう!
どんな実験?
実験手順と種あかし
- たらいの中心からずれた位置に水の入ったトレイを固定しています。トレイの中心には穴があいていて、そこに鉛筆をさして栓にしています。
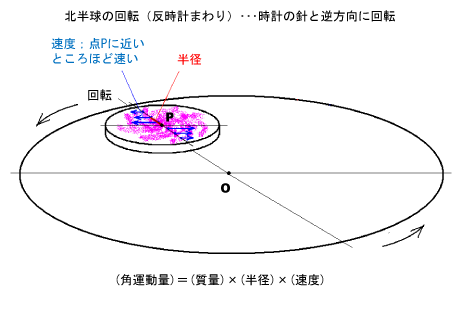
- まず、ターンテーブルを反時計まわり(時計の針と逆の向き)に回転させ、ここにコーヒーに入れるクリームの粉をふりかけて水の流れを見えるようにします。このときの回転方向は地球の北半球と同じ向きです。
- 鉛筆を抜くと穴から水が排水されて、トレイの中の水は回転しながら少しずつ穴(点P)に向かって流れていきます。「内向き流れが回転を速める」の実験と同じように、水は穴(点P)からの半径(距離)が小さくなるにつれて速度を速めていきます。その結果、点Pに近い所ほど半径(OP)に反比例して速く回転します。回転の方向はたらいの回転方向と同じで反時計まわりです。
(以下の説明は大学1、2年生で習う物理の知識が必要です。)
- トレイの中の水が回転する原理は台風や低気圧と同じで、「コリオリの力」によって説明することができます。コリオリの力とは、回転している物体(メリーゴーランドや地球)に乗っている(回転系で)別の物体がその回転体の上で相対運動するときにはたらく見かけの力であり、相対速度に垂直な方向にはたらくものです。
(コリオリの力の大きさ)=2×(質量)×(角速度)×(相対速度の大きさ)
このコリオリの力によって点Pに近づくほど回転が大きくなることが説明できます。ただし、コリオリの力は見かけ上の力であり、実在はしません(回転系で考えるときに作用する見かけ上の力で、この点は遠心力と同様です)。 - トレイの中の水の回転は「角運動量保存則」で説明することもできます。トレイの中の水が持っている角運動量は、①トレイの中心(点P)が点Oのまわりに公転する角運動量(質量はトレイ内の水の全質量、半径はOP、速度は点Pの速度とする角運動量)と②点Pまわりに自転する角運動量(質量は各半径位置の水の質量、半径は点Pからその水までの距離、速度は点Pに対する相対速度とする角運動量)の合計①+②になります。たらいの上に乗って観察すると(回転系)、鉛筆を抜く前はトレイ内の水は回転していないように見えますが、静止した外側で観察すると(慣性系あるいは静止系)たらいの回転数と同じ回転数で点Pまわりに自転しています。つまり、②の角運動量は0ではないのです。水が点Pに近づくと②の角運動量が一定の条件の下、点Pまでの距離に反比例して回転速度が大きくなります。そのため、たらいの回転と同じ向きに渦(自由渦)ができるのです。
- この説明はコリオリの力で説明することと本質的に同じものとなります。つまり、本実験においてコリオリの力は点P(質量中心)まわりの角運動量に関する角運動量保存則によって誘導されるものとなり、回転系で見たときの見かけ上の力となります。遠心力が回転系における見かけの力であり、本質は「慣性の法則」(直線運動を維持しようとする性質)に基づくことと同様です。
- 台風、竜巻、低気圧は中心付近に上昇気流が発生してできます。上昇気流で抜けた分の空気を補うためまわりから空気が集まってきて、実験のトレイの中と同じように内向き流れができます。本実験と同様に中心付近に強い渦ができます。
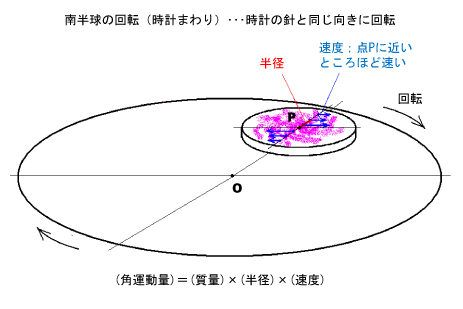
- 南半球では回転方向は北半球と逆になり、台風や竜巻は時計まわりに回転します。
- 高気圧の場合はどのように回転するのでしょうか? 高気圧では中心付近で下降気流が発生し、地上では放射状に拡がる流れができます。点P(質量中心)まわりの角運動量②は保存され、外に拡がるほど回転速度が小さくなります。自転している地球に乗って見ると、自転による回転速度よりも小さくなるため自転とは逆に回っているように観察されます。つまり、低気圧とは逆向きに回転して見えます。北半球では時計まわり、南半球では反時計まわりに回転して見えます。
| 【キーワード】 | 角運動量保存則、自由渦、コリオリの力 |
| 【関連項目】 | 糸を短くすると速く回る、内向き流れが回転を速める、自由渦と強制渦 |
| 【参考】 | 日本機械学会編「流れのふしぎ」講談社ブルーバックス、P52-61. |
更新日:2013.4.4

