流れ 2006年12月号 目次
― 特集: CFDを用いた流体機械最適設計の最前線 ―
| リンク一覧にもどる | |
最適化手法を用いた空調機用熱交換器の開発(熱交換器フィン形状の最適化)
(Optimization of slit shape for heat exchanger)
|
1. はじめに
近年の数値流体力学の普及に伴い,流体問題における最適化についても多くの取組みが行われるようになってきた (1) ~ (3) .特にオフラインで行える形状最適化は,最近では設計開発現場にも適用され始めているが,設計変数が多く,応答が極めて複雑な場合には,最適解を得るために多くの計算回数が必要となるだけではなく, GA ( Genetic Algorithm )などの確率論的な手法を使わざるを得ないため,最適解そのものに対する信頼性が低下することがある.また,最適化プロセスにより得られた膨大なサンプリングデータを吟味し,有効に利用する方法が少ないため,現在のところ定着するまでには至っていないと言える.
本稿は,上記のような現状を踏まえ,多くの設計変数から成る多峰性解空間を有する熱流体問題に対して,大域な解空間から複数の小域な解空間を抽出した後,それぞれの解空間にて最適化を行う新たな最適化のアプローチを提案,空調機用熱交換器フィンの開発に適用し,その有効性を検証した結果を報告する.
2. 提案する最適化プロセス
最適解の探索をより早く行う,また,確率論的な最適化手法において最適解の信頼性を向上させる単純な方法として,対象とする解空間の範囲を限定する方法が考えられる.対象とする解空間が限定されれば,探索に多様性を持たせる必要性が低下し,また,場合によっては数理的な最適化手法を使うことが可能となる.本稿では,対象とする解空間を人為的に限定するのではなく,応答局面( Response Surface Model )を利用したデータマイニングを行うことにより,大域な解空間から複数の小域な解空間を抽出する方法を提案する(図 1 ).
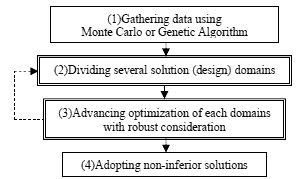
Fig.1 Outline of optimization procedure .
なお,熱流体数値解析には汎用熱流体解析ソフト STAR-CD ( CD-Adapco Korea )を,プロセスの統合化には Unix シェルプログラムを,データのサンプリングと最適化エンジンには汎用最適化ソフト modeFRONTIER ( CD-Adapco Japan )および iSIGHT ( Engineous Japan )を用いた.
2.1 データのサンプリング
解(設計)空間を分割するためには多数,かつ空間に一様なデータが必要となる.本稿では, 2 次の応答局面を利用して解空間を分割するため,応答局面の精度を考慮した場合,設計変数の数を ![]() ,解空間の分割数を
,解空間の分割数を![]() とすると,サンプリング数
とすると,サンプリング数 ![]() は
は
(1)
ここで,![]() は
は![]() から 2 個の組み合わせを選ぶコンビネーション関数を示している. 例えば,設計変数が 24 ,解空間の分割数を 6 とした場合,サンプリング数
から 2 個の組み合わせを選ぶコンビネーション関数を示している. 例えば,設計変数が 24 ,解空間の分割数を 6 とした場合,サンプリング数![]() は 3900 個以上となる.
は 3900 個以上となる.
2.2 解空間の分割(抽出)
本稿で用いた解空間の分割(抽出)方法の概要を図 2 に示す.
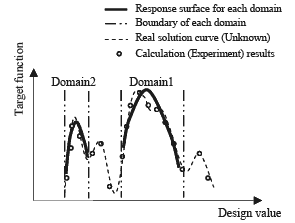
Fig.2 Concept of dividing-domain method.
解空間を任意に分割した後,それぞれの領域について応答局面を作成する.例えば , 応答関数として 2 次多項式を用いた場合,応答局面は次のようになる.
(2)
ここで,相関式と解空間に実際に存在するデータとの整合性を評価する指標として,次式に示す自由度調整済み決定係数を用いる.これは 0 から 1 の間の値を取り, 1 に近いほど良い相関であることを示している.
(3)
ここで,
応答
の平均値まわりの変動:
(4)
決定係数:
(5)
残差平方和:
回帰二乗和:
(6)
それぞれの領域における上記応答局面の誤差を最小化するように解空間の分割(抽出)を繰り返して行う.その際,各データと領域の中心との距離を次式で算出し( 2 次元の場合),境界近傍にあり,かつ中心からの距離が設定以上のデータに関しては,複数の領域に存在するように分割(抽出)を行う (4) .
(7)
2.3 各領域における最適化検討
応答局面の誤差が小さい領域に対しては非線形計画法などの数理的な手法を,誤差が大きい領域に対しては SA ( Simulated Annealing )などの確率論的な手法を用いて最適化を進める.ここでの最適化は,影響因子を考慮した設計変数の絞込みや比較的優先度の低い目的関数の追加,あるいはロバスト性の評価など,実際の適用を意識した検討を行う.
2.4 非劣解の採択と設計への反映
各領域における最適化プロセスによって得られたデータ群を用いて,解空間の更新と領域の再分割(抽出)を行い,各領域における非劣解を採択する.なお,各領域において影響因子を考慮した高精度な近似式を設計式としてまとめることにより , 設計データベースとして活用することが可能となる.
3. 空調機用熱交換器フィン開発への適用
次に,上述の最適化プロセスを空調機用熱交換器フィン開発に適用した事例を説明する .
3.1 最適化問題の設定
対象とする熱交換器フィンは,熱伝達性能が高く,圧力損失(通風抵抗)が低いものが高性能化の最優先次項となる.本稿では伝熱管(パイプ)間に切り起こし(スリット)を設け,この形状を最適化することでこのトレードオフ問題に対応する.
3.2 設計変数
フィンの切り起こしを構成する設計変数を 図 3 に示す.本稿では,フィンカラー部の外径 DcA ,段ピッチ Dp ,列ピッチ Lp ,フィン厚さ tf ,フィンピッチ fp は変更せず,前面風速を 1.5 ( m/s )に設定した場合の切り起こしの形状,即ち,切り起こしの位置 Ds ,長さ Ls ,幅 Ws ,高さ Hs ,角度θ1 ,θ2 を最適化した . 例えば , 切り起こしの数が 3 個の場合 , 設計変数の数は 18 個となる.
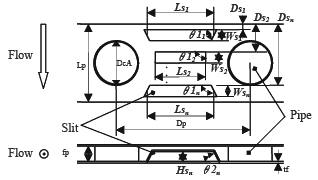
Fig.3 Design variables for fin shape.
3.3 解析自動実行システム
図 4 に本解析を自動実行するために構築したシステムのフローチャートを示す.前項で示した設計変数を無作為に設定した場合,幾何学的に成立しない組み合わせが多数発生することが予想される.そこで,設計変数を直接的に設定するのではなく,幾何形状エラーが発生しない設計変数の組み合わせを任意に定義することが可能なパラメトリックプログラムを作成し,そのプログラムの入力変数を最適化のパラメータとした.解析モデルの作成とポスト処理は Prostar のマクロ機能を利用し,解析の収束判定には Star-CD の残渣と出入口 境界における圧力差と温度差をモニタすることにより行った.
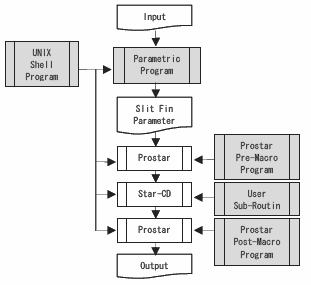
Fig. 4 Flow chart of integrated analysis process.
図 5 に,本検討で開発した上述のマクロプログラムを用いて作成した解析モデルの一例を,図 6 に同一形状におけるメッシュサイズと解の関係を示す.
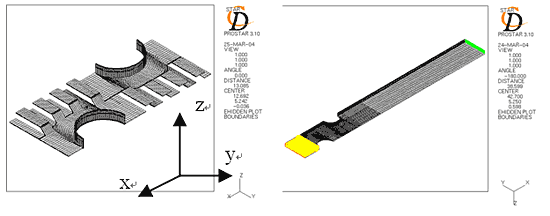
Fig.5 Example of an analysis model.
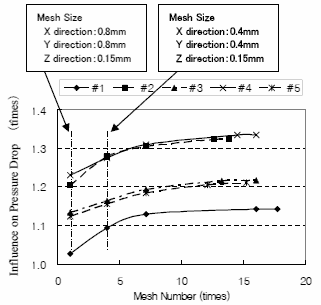
Fig.6 Influence of mesh size
次式( 8 )で求めたレイノルズ数は,前面風速が 1.0 ( m/s )から 2.0 ( m/s )の場合, 約 160 から 330 の値となる.従って,本解析は層流として取り扱うため,格子サイズを小さくする,即ち,格子数を多くすることにより解析精度が向上することは自明であるが,それに伴う計算時間の増加は多くの解析を必要とする最適化検討において深刻な問題となる.そこで,解析結果が相対的に安定する x 方向サイズ 0.4mm,y 方向サイズ 0.4mm,z 方向サイズ 0.15mm の格子サイズを選択することにした .
(8)
ここで, U はフィン前面風速,νは動粘性係数, Dec は次式より算出するプレートフィン&チューブの等価直径を示している (5) .
(9)
ここで, S1 , S2 はそれぞれ列ピッチ(流れ方向)と段ピッチ(流れに垂直な方向)を示している.
3.4 データのサンプリング
図 7 に Monte Carlo 法,および Genetic Algorithm を用いてサンプリングしたデータ群( 8000 点)を,本稿で提案した手法を用いて 6 つの解空間に分割した結果を示す.なお,本データはパイプ径,段ピッチ,列ピッチ,フィン厚さが同じ構成で,フィンピッチのみ異なる( 1.2mm )切り起こしの無いフィン(プレートタイプ)の性能を基準とした場合のフィンピッチ 1.5 ( mm )の切り起こしを有するフィンの性能(熱伝達率,圧力損失)を示している.なお,切り起こしの数は 3 本と 4 本の場合についてのみ検討を行った.
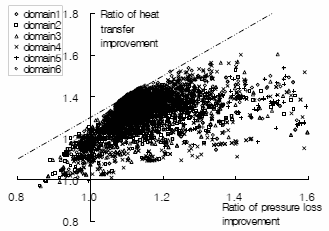
Fig.7 Sampled dataset applied data-mining.
4. 騒音評価方法の提案
一方,実際の空調機,特に室内機に熱交換器を実装する際には,基本性能(圧力損失・熱伝達率)以外に騒音等を評価する必要がある.特に近年の室内機のコンパクト化により,熱交換器とファンが近接する傾向にあり,その結果,騒音が増大することが少なくない.そこで,熱交換器に起因する騒音発生メカニズムを推定し,簡易的に評価する方法を提案することにより,最適化の目的関数の一つとして扱うことを可能とした.
4.1 騒音発生原因の推定 図 8 にフィンピッチ 1.5 ( mm )の従来の切り起こし形状を有する当社フィンを示す.

Fig.8 Present fin shape (Samsung Electronics Co.).
次に,フィンピッチ 1.2 ( mm )の切り起こしの無いフィン(プレートタイプ)と 上記 切り起こし形状を有するフィンを,それぞれ当社製品に実装し, 1320 回転で運転した際の騒音測定結果を図 9 に示す.
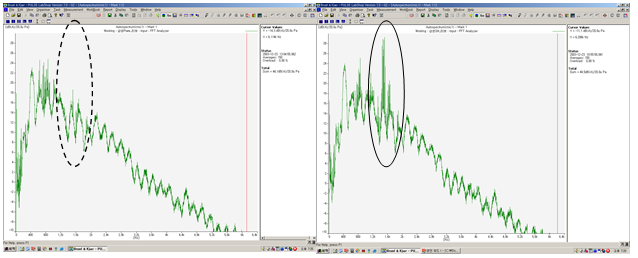 |
|
| (a)Plate fin | (b)Present slit fin |
Fig.9 Result of noise measurement (1320rpm).
従来の切り起こし形状を有するフィンでは 1.1 ( kHz )から 1.6 ( kHz )の範囲に,切り起こしの無いフィンでは確認することができないピーク(ファン干渉音)が存在することが分かる.上記の実験条件は熱交換器フィンのみが異なることから,このピークは熱交換器フィンによって作られる不均一な速度場をファンブレードが移動する際に生じる非定常な圧力変動によって発生すると推定することが出来る(図 10 ).
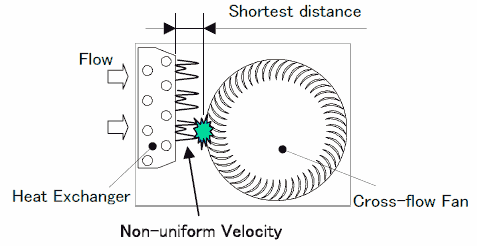
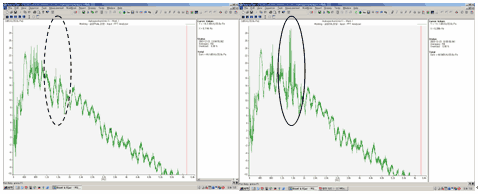
Fig.10 Conception of a mechanism which a noise generates.
4.2 定常解析による評価方法
上述の推定に基づき,まず,熱流体数値解析を行い,熱交換器下流側の速度場を求めた.解析には 汎用熱流体解析ソフト STAR-CD を用い,熱交換器パイプ段方向ピッチの半分をモデル化した.実験を行った製品において,熱交換器とファンが最も近接する距離は 15.5 ( mm )であることから,フィン端部より下流側に 15.5 ( mm )の位置における速度分布を図 11 に示す.
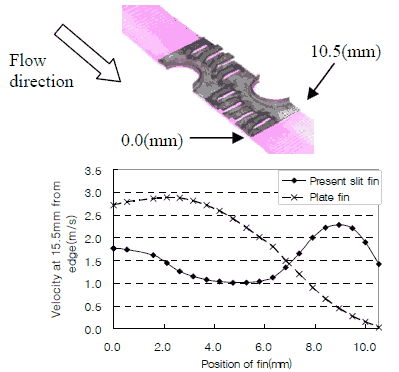
Fig.11 Velocity profiles at fin-downstream side
実際にはフィンによって作られる上記の速度場をファンブレードが移動するのであるが,上記速度場のフィン位置を示す軸を時間軸に変更するために , ここでは固定されたブレードに対して周期的に速度が変動していると考える(図 12 ).即ち,図 11 で示した位置に関する速度データを,クロスフローファン直径 86 ( mm )と回転数 1320 ( rpm )を用いて時系列データに変換する.次に,変換後の速度データに対して離散フーリエ変換を行った結果を図 13 に示す.
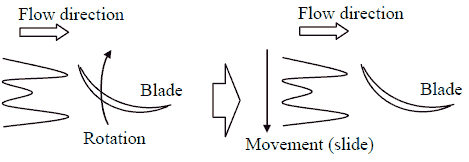
Fig.12 Relative relation between velocity distribution and blade
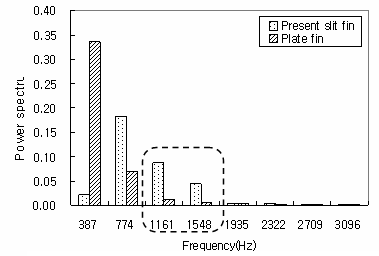
Fig.13 Number at each frequency using DFT
図 9 で示した熱交換器に起因すると考えられる騒音の周波数範囲 1.1 ( kHz )から 1.6 ( kHz )において,従来の切り起こし形状を有するフィンでは切り起こしの無いフィンの 5 倍から 10 倍の値を示しており,騒音の発生原因と密接な関係があると考えられる.
5. 最適な切り起こし形状の決定
3 章にて示した分割(抽出)後のそれぞれの領域において,非線形計画法を適用して最適化を行った結果を図 14 に示す.その際,騒音低減のために 4 章にて示した評価手法(フィン後流の速度分布の DFT 分析)を目的関数に加えた.また,凝縮水の排水性向上を目的として,切り起こし部の総エッジ長さの最小化を加えるとともに,スリット寸法に対するロバスト性も考慮し,実際の加工に対する安定した解を探索した.なお,図中のデータは既にサンプリングされたデータと重複するもの,および二点鎖線以下のデータは取り除いている.
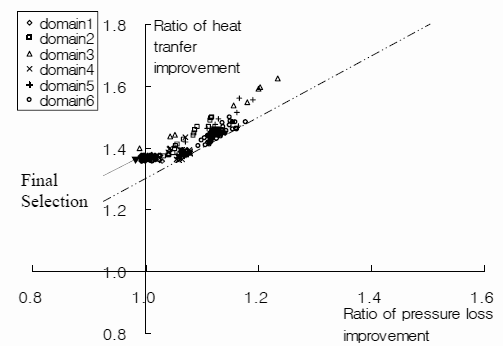
Fig.14 Result of optimization for each
図 15 に本最適化により決定した切り起こし形状を示す.このフィンの幾何的な特徴は,上流側に短く,幅の狭い切り起こしが 2 本,下流側に長く,フィンカラー径の約 1/3 に相当する幅の広い切り起こし 1 本が配置されていることである.

Fig.15 Fin shape determined by optimization
6. 実験による検証
6.1 基本性能の検証
図 16 に従来の切り起こし形状を有するフィンと最適化した切り起こし形状を有するフィンの単体性能を比較した結果を示す.実験に用いた熱交換器は, 2 列 12 段で幅 400 ( mm ),前面風速 1.5 ( m/s )の冷房条件における測定結果を フィンピッチ 1.2 ( mm )の切り起こしの無いフィン性能を基準として比較したものである.
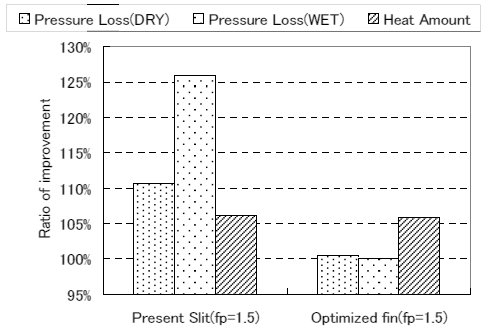
Fig.16 Element test results at cooling.
最適化した切り起こし形状を有するフィンは,従来の切り起こし形状を有するフィンと比較すると,熱交換量は同等ながら,圧力損失はドライ時で約 10 %,ウェット時で約 25 %向上することが確認できた.
また,最適化を行う際に採択した格子サイズのさらに 1/2 のサイズを用いて解析した結果( 3.3 節参照)とドライ条件における実験結果を比較すると,解析精度は圧力損失では約 +2 %,平均熱伝達率では約 +3 %であることが確認できた.
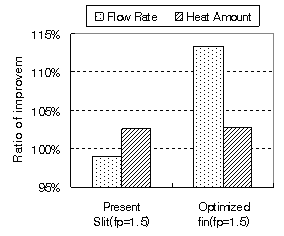
次に,図 17 に フィンピッチ 1.5 ( mm )の従来の切り起こし形状を有するフィンと最適化した切り起こし形状を有するフィンを,当社製品( 製品A , 製品B )に実装した結果を示す.
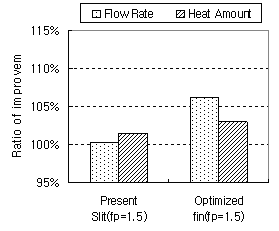 |
 |
| ( a ) Apply to Samsung air conditioner (製品A). | ( b ) Apply to Samsung air conditioner (製品B). |
Fig.17 Assembly test results at cooling
最適化した切り起こし形状を有するフィンを当社製品に実装した結果,従来の切り起こし形状を有するフィンと比較すると, 製品A の場合は風量が約 7 %, 製品B の場合は風量が約 15 %増加することが確認できた.なお,本来は風量増加に伴う熱交換量の増加が考えられるが,本実験は従来の切り起こし形状を有するフィンに対して冷凍サイクルの設定を行っていたため,熱交換量は微増に留まった.
6.2 騒音の検証
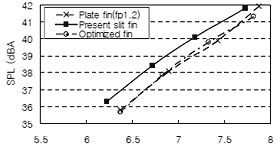
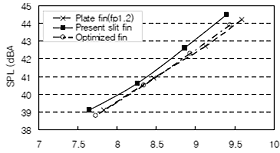
図 18 に最適化した切り起こし形状を有するフィンを当社製品に実装し, 1320 回転で運転した際の騒音測定結果を,図 19 にその周波数スペクトルを示す.
 |
 |
| ( a ) Apply to Samsung air conditioner (製品A). | ( b ) Apply to Samsung air conditioner (製品B). |
Fig.18 Assembly test results at 1320rpm.
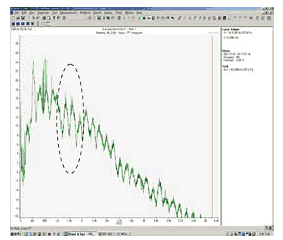
Fig.19 Result of noise measurement (1320rpm)
最適化した切り起こし形状を有するフィンを当社製品に実装した結果,従来の切り起こし形状を有するフィンと比較すると, 製品A の場合は約 1 ( dbA ), 製品B の場合は約 0.5 ( dbA )低減することが確認できた.これは,切り起こしの無いフィンと同レベルであることが分かる.また,周波数範囲 1.1 ( kHz )から 1.6 ( kHz )におけるピーク(ファン干渉音)は認められなかった.
7. 考察
7.1 一般的な切り起こしの設計方法
本章では,まず一般的な切り起こしの設計方法について言及し,最適化した切り起こし形状を有するフィンの特徴と比較することにより,その性能について詳細に分析する.
まず,一般的な切り起こし部の熱伝達率は次式のように考えることが出来る (6) .
(10)
ここで, k は熱伝導率( 0.0261W/mk ), Pr はプラントル数( 0.72 )であり, Re a は次式で示される.
今,切り起こしの幅 Ws の範囲を次式で定義し,
(11)
(10) 式に代入して整理すると,切り起こし部の熱伝達率は
(12)
一方,切り起こしがないフィンの熱伝達率は簡便に次式のように考えることが出来る (6) .
(13)
また,列ピッチ Lp 間に存在する切り起こしの個数を Ns とすると,有効熱伝達率は式 (12) と (13) の面積加重平均と考えることが出来る.
(14)
従って,切り起こしの個数によって増加する平均熱伝達率の割合は次式となる.
(15)
以上から,切り起こしの個数 Ns に比例する形で熱伝達率が増加することが分かる.ただし,熱伝達率と伝熱量そのものは比例関係にはなく,空気が下流側に進む過程において空気温度がフィン面の 温 度に近くなり, 伝熱量が一定値に漸近する.具体的には, 伝熱量は次式で 示される .
(16)
ここで,ρは密度( 1.2kg/ m 3 ), cp は比熱( 1004J/kg ・ K ), NTU は伝熱ユニット数( Number of Transfer Unit )であり次式で示される.
(17)
Np は流れ方向に設置する伝熱管の列数である. Heff は式 (14) で示したように次式で示される.
(18)
従って,伝熱量および切り起こしの個数によって増加する伝熱量の割合は
(19)
(20)
ただし, NTU0 は切り起こしの数が Ns=0 の場合の NTU である.
次に,切り起こしのないフィン間の圧力損失は次式のように考えることが出来る (7) .
(21)
ここで,γは常温常圧空気の比重量, g は重力加速度であり, Refp は次式で示される.
一方,切り起こし部分の圧力損失は,
(22)
また,全体の圧力損失は
(23)
従って,切り起こしの個数によって増加する圧力損失の割合は,
(24)
今, (11) 式で示した切り起こしの幅 Ws の範囲を, (24) 式に代入して整理すると,
(25)
即ち,切り起こしの個 数 Ns に比例する形で 圧 力損失が 増 加することが分かる.
熱交換器フィンにおける一般的な切り起こしの設計方法は, (20) 式に示した切り起こしの個数によって増加する伝熱量の割合が, (25) 式に示した切り起こしの個数によって増加する圧力損失の割合を超えるように,切り起こしの個数を決める.
7.2 熱伝達性能
図 20 に熱流体解析により求めたフィンピッチ 1.5 ( mm )の従来の切り起こし形状を有するフィンと最適化した切り起こし形状を有するフィンの各切り起こしによって生じる伝熱量の推移を示す.前縁からの切り起こしの位置が 4 番目までが伝熱管の一列目, 5 番目以降が伝熱管の二列目を示している.
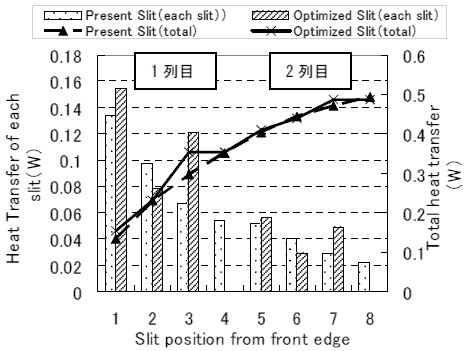
Fig.20 Trend of heat transfer made by each slit.
従来の 切り起こし形状を有するフィンは,上述したように空気が下流に進むにつれて空気温度がフィン温度に近づくため,各切り起こしでの熱交換量が漸近減少しながら,全体としての熱交換量が増加していることが分かる.一方,最適化した切り起こし形状を有するフィンは,前縁から 3 番目の切り起こしにおける熱交換量が 2 番目の切り起こしにおける熱交換量を上回っており,伝熱のパターンが異なっていることが分かる.
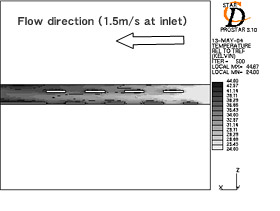
次に,伝熱現象の詳細を検討するために 従来の切り起こし形状を有するフィンと最適化した切り起こし形状を有するフィンのフィン中央断面の空気温度分布とフィン表面の熱流束分布を図 21 に示す.
 |
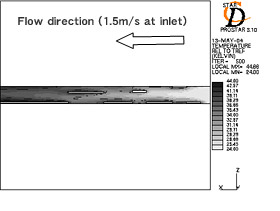 |
| (a) Temperature contour of air (present slit). | (b) Temperature contour of air (optimized slit). |
 |
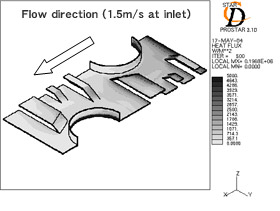 |
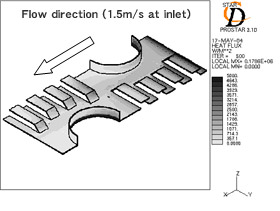
| (c) Heat flux contour on fin surface (present slit). | (d) Heat Flux contour on fin surface (optimized slit). |
Fig.21 Characteristics of heat transfer for each fin.
従来の 切り起こし形状を有するフィンでは,前縁から 2 番目以降の切り起こしは,全て上流側に位置する切り起こしの温度境界層の影響を受けているが,最適化した切り起こし形状を有するフィンはそれぞれの切り起こしで温度境界層の更新が行われていることが分かる.また,最適化した切り起こし形状を有するフィンにおいて,前縁から 3 番目の切り起こしに注目すると,切り起こしの上流部で十分な前縁効果による熱伝達性能の向上が得られているのみではなく,後流側のフィンベース部でも前縁効果による熱伝達性能の向上が得られていることが分かる.即ち,切り起こしの後流側のフィンベース部において,切り起こしと同様の効果が得られていると考えることができ,この伝熱パターンが最適化した切り起こし形状を有するフィンの性能が向上した要因であると考えることが出来る.
7.3 圧力損失性能
図 22 に熱流体解析により求めたフィンピッチ 1.5 ( mm )の従来の切り起こし形状を有するフィンと最適化した切り起こし形状を有するフィンの各切り起こしによって生じる圧力損失の推移を示す.
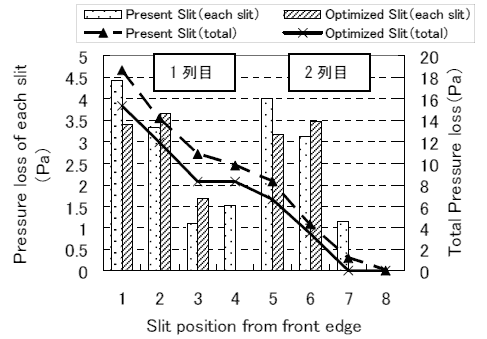
Fig.22 Trend of pressure loss made by each slit.
従来の 切り起こし形状を有するフィンと 最適化した切り起こし形状を有するフィンでは,圧力損失のパターンはほぼ同じと考えることができ,切り起こしの個数がそのまま トータルの圧力損失性能の差となっていることが分かる.
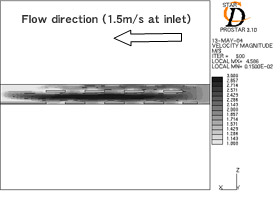
次に,圧力損失性能の詳細を見るために 従来の切り起こし形状を有するフィンと最適化した切り起こし形状を有するフィンのフィン中央断面の空気速度分布を図 23 に示す.
 |
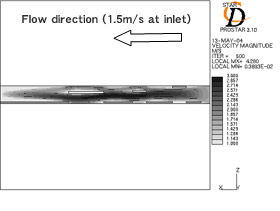 |
| (a) Temperature contour of air (present slit). | (b) Temperature contour of air (optimized slit). |
Fig.23 Characteristics of pressure loss for each fin
従来の 切り起こし形状を有するフィンのフィン間最大流速が約 4.6 ( m/s )であるのに対して,最適化した切り起こし形状を有するフィンのフィン間最大流速は約 4.1 ( m/s )であり,最適化した切り起こし形状を有するフィンの流れが一様化していることが分かる.また,切り起こしによって増速した空気流の静圧が,前縁から 3 番目の切り起こしの幅が広いために局所的に回復し,その結果,空気流が一様となり,前項で述べたように切り起こしの後流側のフィンベース部が切り起こし部と同様な流れ構造となっていることが確認できる.
前述したように,一般的なフィンの切り起こしは,切り起こしの個数による伝熱量の増加度合いが圧力損失の増加度合いを超えるように設計されるが,最適化した切り起こし形状を有するフィンは,特に前縁から 3 番目の切り起こしによる熱伝達性能を最大化するような流れ構造を, 2 番目の切り起こしで形成しており,伝熱のパターンにおいて従来の概念とは異なるフィンであることが分かる.
7.4 ファン干渉音
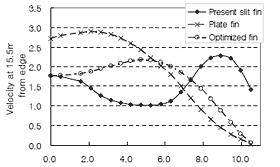
図 24 に 最適化した切り起こし形状を有するフィンの フィン端部から下流側 15.5 ( mm )における速度場を,図 25 に上記速度を 4 章で示した 方法で算出した周波数範囲 1.1 ( kHz )から 1.6 ( kHz )の数値を示す.
 |
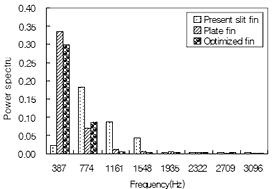 |
| Fig.24 Velocity profiles at fin-downstream side | Fig.25 Number at each frequency using DFT |
最適化した切り起こしを有するフィンのフィン端部から下流側 15.5 ( mm )における速度場は , 従来の切り起こしを有するフィンや切り起こしのないフィンとも異なるが , 4 章で示した 方法で算出したスペクトルでは , 最適化した切り起こしを有するフィンと切り起こしのないフィンでほぼ同様の傾向を示しており , ファン干渉音の有無と一致することから , 本稿で示したファン干渉音の制御方法は有効であると考えられる .
8 まとめ
多くの設計変数から成る多峰性解空間を有する熱流体問題に対して新たな最適化のアプローチを提案し,その有効性を空調機用熱交換器フィンの最適化問題において示した.その結果,最適化した切り起こし形状を有するフィンは,
(1) 熱交換器単体において,従来の切り起こし形状を有するフィンと比較すると,熱交換量は同等ながら圧力損失はドライ時で約 10 %,ウェット時で約 25 %低減した.
(2) 当社製品に実装した場合,従来の切り起こし形状を有するフィンと比較すると, 製品A では風量が約 7 %, 製品B では風量が約 15 %増加した.
また , 熱交換器に起因する騒音発生メカニズムを推定し , 簡易的な制御方法を開発し , 最適化の目的関数に加えることにより ,
(3) 当社製品に実装した場合,従来の切り起こし形状を有するフィンと比較すると, 製品A では騒音が約 1 ( dbA ), 製品B では騒音が約 0.5 ( dbA )低減し , ファン干渉音スペクトルのレベルを切り起こしのないフィンと同等レベルに低減した .
以上の結果から本提案の最適化手法は,複雑な大域な解空間から複数の小域な解空間を抽出することにより,それぞれ特徴の異なる非劣解を合理的に取得することが可能であることを,また,最適化の初期過程においては優先度の高い目的関数のみを,最終的な最適化過程では優先度の低い目的関数の考慮を行うという独立した 2 段階の最適化を行うことにより,最適解を効率的に取得することが可能であることを示し,実設計において非常に有効な手法であると考えられる.
参考文献




