流れ　2007年4月号　目次

―　特別寄稿　　― 文化功労者としての顕彰にさいして　―研究成果とその波及効果― 伊藤英覺（東北大学名誉教授） ―　特集：　自動車と流れ　　― 自動車の計算流体力学 安木 剛（トヨタ自動車） CFDによる自動車エンジンルーム内の熱環境予測 小森谷 徹（富士重工業） カーエアコン性能を最大化するためのCAE 浅野 秀夫，須藤 知宏（デンソー） 自動車用流体機械における流れの数値解析 近藤 靖裕，河上 充佳，増田 糧（豊田中央研究所） 自動車空力騒音のシミュレーション 堀之内 成明，稲垣 昌英，加藤 由博（豊田中央研究所） 自動車周りの非定常流れ 小島　成（カレッジ・マスターハンズ），亀本　喬司（横浜国立大学） 編集後記 川口清司（富山大学）、安藤俊剛（三重大学）、磯　良行（石川島播磨重工）、 宇都宮浩司（広島工業大学）、東村哲志（シーディー・アダプコ・ジャパン） 　｜　リンク一覧にもどる　｜

 

自動車の計算流体力学

安木　剛
トヨタ自動車

１． はじめに

　日本の自動車メーカーは１９８０年代に有限体積法や有限差分法による計算流体力学を自動車開発に応用する研究を開始した . 　これらの主な研究目的は，外形スタイリングもしくは室内意匠に性能が大きく依存する

　　① エンジンルーム内冷却
　　② 室内空調
　　③ 空気抵抗

の予測と改善であった . 　１９９０年代では上記の①と②はｋ－ε乱流モデルと有限体積法を組み合わせて計算コードにより自動車開発に応用された . 　③には精度確保困難かつ計算時間が①と②に較べて過大という２つの課題があった . 　２０００年代では自動車から排出されるＣＯ２低減の一つの手段として③の予測と改善のため計算流体力学への期待が高まっている .

　本稿では①，②，③の歩みと現状について述べる .

２．エンジンルーム内冷却

　１９８０年代末から自動車の開発に応用される . 　前回りの外形スタイリングと標記性能の両立のため，外形スタイリング検討段階でラジエータ・コンデンサを通過する風流を計算流体力学で予測し ( 図１ ) ，必要な場合は外形スタイリングを計算流体力学の結果を参考に修正する .

　エンジルーム内に配置された部品の温度予測にも応用されつつある .

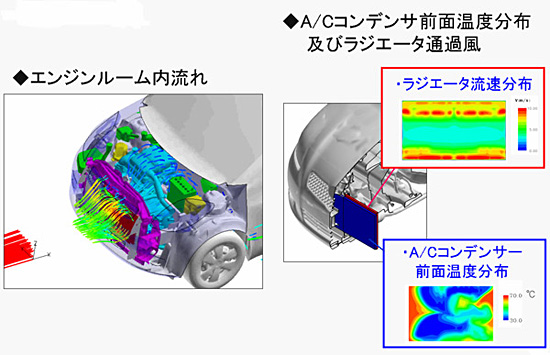
Fig. 1: Flow through radiator

３．室内空調

　１９９０年代当初にデフロスタの性能予測が自動車の開発に応用された . 　その後，室内意匠と各種空調性能（クーラーフェース，デフロスタ等）を室内意匠検討段階で予測し（図２），必要な場合は計算流体力学の結果を参考に，ダクト噴出し位置・形状を修正する .

　温度と風速などの計測可能な物理量のみならず，人が感じる「温感」も評価指標として使用する .

Fig. 2: Flow in cabin

４．　空気抵抗

(1) 空気抵抗係数の推移

　１９８０年代に計算流体力学による自動車の空気抵抗予測の研究は外形スタイリング改良から開始された . 　１９８０年では市販される乗用車の空気抵抗係数（以後， CD ）の分布は０．３２から０．４５までであったが，２０００年では０ . ２６から０．３５までに減少した . 　空気抵抗係数の減少は自動車から排出されるＣＯ２低減の一つの手段であるため，今後ますます減少する傾向にあると推定される ( 図３ ).

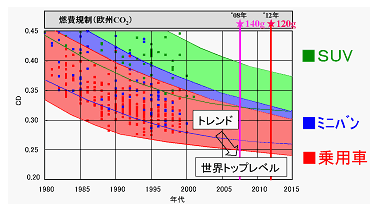
Fig. 3: Distribution of air drug coefficient of vehicle

 

　１９８０年代に比べて空気抵抗係数が減少した２０００年代の乗用車の空気抵抗発生源は大きく分けて，①外形，②エンジンルーム通気，③床下・タイヤ　である ( 図４ ). 　空気抵抗は外形スタイリングに大きく依存するとはもはや断言できす，②エンジンルーム通気と③床下・タイヤの空気抵抗発生源に対する配慮が必要である . 　このため，①のみならず，②と③を考慮できる計算流体力学の手法が必要となった . 　このため，外形だけてなく，エンジンルームと床下・タイヤの形状を詳細に再現した計算モデルを作成する（図５） .

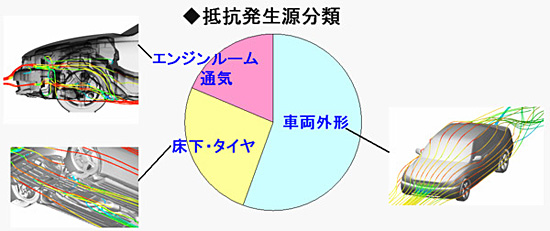
Fig. 4: Component air drug of vehicle

 

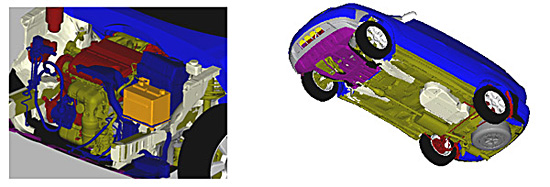
Fig. 5: Engine compartment and under-floor of CFD model

 

(2) 予測精度の課題

　空気抵抗の予測事例の大半は誤差±５％の範囲内であるが，一部の例において実験結果と乖離する場合がある . 　この場合，車両背面での圧力過少評価が主な原因である（図６） .

車両背面での圧力を過少評価する原因を解明するため

　　① 剥離部計算格子，
　　② 風洞内の圧力分布，
　　③ 非定常流れの影響

を調査した .

Fig. 6: Correlation of drug coefficient and pressure on the back door

 

(3) 剥離部計算格子の影響

　基礎研究用に作成された３次元の形状簡略化モデルを用いて，車両後部剥離位置と計算格子サイズ等の影響を確認した . 　バックドア回りの実験の流れに近づけるには剥離位置近傍の計算格子サイズの調整が必要であることが判明したが，バックドア回りの圧力予測精度の改善は小さい（図７） .

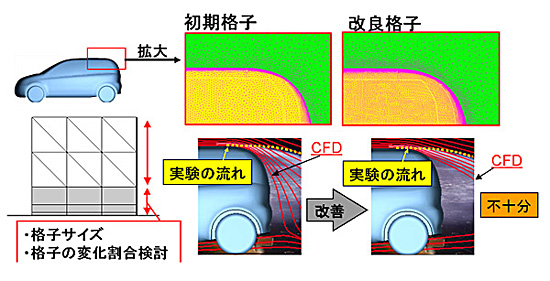
Fig. 7: Grid size and flow around back door

 

(4) 風洞内の圧力分布の影響

　風洞の細部をモデル化し計算流体力学により圧力分布を算出たところ，良好に実験と対応した（図 8 ） . この圧力分布に車両のシルエットを重ねることにより，車高と全長が大きい車両では風洞内部の圧力分布がバックドア回りの圧力に影響を与えると推定される . 　車両まわりの計算空間は計測される風洞と同一にする必要が判明した .

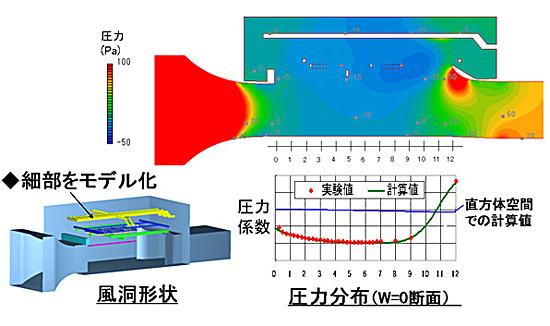
Fig. 8: Pressure distribution in the wind tunnel

 

(5) 非定常流れの影響

　図５のエンジンルームと床下・タイヤの形状を詳細に再現した計算モデルに図７と同様に計算格子サイズを調整し，図８の風洞にてｋ－εモデルで有限体積法により定常流として計算した結果，依然としてバックドア回りの圧力予測精度が不足である（図９の左） .LES による非定常流れ計算では，バックドア回りの圧力予測精度が改善され，ルーフスポイラーの形状変更の効果も再現できた（図９の右） .

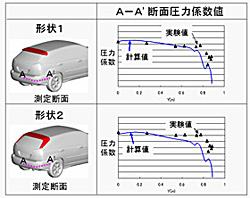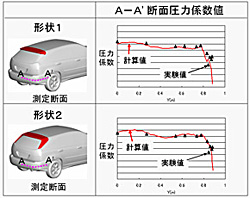by steady flow analysis	by unsteady flow analysis
Fig. 9 Correlation of pressure on the back door

 

５．今後の展望

　自動車の空気抵抗を低減するには、

　　①空気抵抗係数が目標からどれだけ乖離するか？
　　②目標から乖離の原因はどこにあるか？
　　③その原因を解消すればどれだけ目標に漸近するか？

を把握するのが一連のプロセスである。①と③は正確な計算流体力学で算出された空気抵抗係数から知ることができ、②を正確に特定するには計算流体力学から算出される速度（ U,V,W ）と圧力（ P ）だけでは困難な場合がある。例えば、図１０のなかでケース３がもっとも空気抵抗係数が小さいが、車両中央断面の圧力分布にはケース１，２との有意な差が見られない。その他の速度分布などでも同様である。

　従来は、空気抵抗が目標と乖離した場合、自動車のプロファイルを系統的に変更し、帰納的に最適なプロファイルを求めた。その後、車両表面のフィレット R などを調整することで空気抵抗を低減した。

　図１０に示したように、エンジンルームと床下・タイヤの空気抵抗を低減するには上記の従来方法の適用が困難である。自動車まわりの流れ場から自動車の空気抵抗・揚力の原因となる流れ（渦管、渦層）を選別し、その発生場所が判明すればエンジンルームと床下・タイヤでも②を正確に特定できる可能性がある。図１０のケース１を例にとると、この自動車まわりの流れ場には車両の後方のみならず，前方、下方、上方、側方に１０個以上の渦管、渦層が観察される。これらの渦管、渦層の発生場所と強さを一定の精度で特定し、自動車の空気抵抗・揚力との関係を理論的に解明するのが今後の課題と考える。

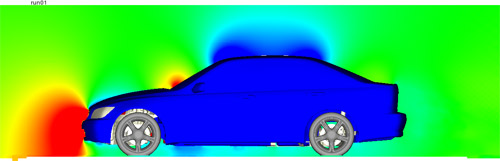
Case 1

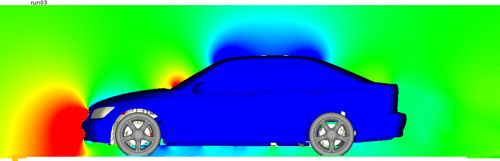
Case 2

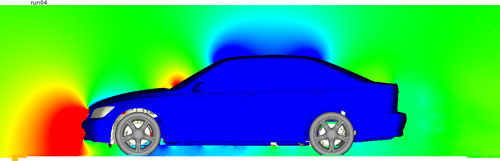
Case 3

Fig. 10 Pressure distribution at center section