乱流遷移解明から機械学習応用まで（東京理科大学，塚原研究室）

東京理科大学　創域理工学部　機械航空宇宙工学科 教授　塚原　隆裕 〒278-8510 千葉県野田市山崎2641 URL : https://www.rs.tus.ac.jp/~t2lab/ E-mail : tsuka[at]rs.tus.ac.jp　　※[at]を@に変えてお送りください．            キーワード：乱流遷移，DNS，複雑流，血流，機械学習

研究室の特色

　題目では，あたかも“乱流遷移”から“機械学習”までの一次元的で一方向的な研究の発展を思わせますが，当研究室ではあらゆる熱流体現象に関心を持って，2次元的もとい多方向に手広く基礎研究から応用研究まで研究活動を展開しています．主に数値流体力学シミュレーションをメインツールとして，また大学院生を主力メンバーとして，学術的および実学的な人類への貢献を心掛けて活動しています．．．とは言え，以下の拙文が人類に有益かは疑問ですが，当研究室を赤裸々に紹介して参ります．

研究室概要

　身近な流体である水や空気の運動は，水道や気象に限らず，あらゆる場面で重要な物理現象として扱われます．航空機や船舶の性能，各種プラント（電力・薬品・食品）の安全性，空調換気の快適性に直接絡んできます．また，血流や呼吸も重要な流体輸送です．それらの多くは，“乱流”と呼ばれる複雑な運動状態にあるか，ときには流動依存の物性を呈する非ニュートン流体や固・気・液の混相状態にある複雑流です．その流動状態を理論的（解析的）に解いたり，さらには予測や制御をしたりすることは，困難を極める挑戦的な課題です．そこで，当研究室ではスーパーコンピュータ（スパコン）を駆使した数値流体力学（CFD）シミュレーション等により，乱流と複雑流の解明にアプローチしています．例えば，発電プラント内の冷却材流れ，航空機翼周りの流れ，マイクロ界面張力駆動の流れ，冠動脈カテーテル治療後の血流解析，有害物質等の漏洩と乱流拡散の予測，等々（詳細は後述）．最近では，シミュレーション中に蓄積されるビッグデータに基づいた機械学習（AI）の応用にも挑戦しています．スパコンとAIを駆使して複雑流動・乱流物理の本質を理解し，省エネルギ・医療高度化・環境保全への寄与を目指しています．

研究室構成

　2023年10月現在は，卒研生6名，修士一年7名，修士二年6名，博士一年～三年が各1名，そしてスタッフ（教授1名，助教１名，秘書1名）含めて合計25名の体制です．助教には，大阪大学とÉcole Centrale de Lyonから博士号（ダブル・ディグリープログラム）を授与された荒木亮氏をこの10月に迎え，研究指導に加わってもらっています．博士課程学生は日本学術振興会特別研究員DC2，JST次世代研究者挑戦的研究プログラム支援学生と様々です．私立大学らしく教員数に対する学生数は多めですが，学生間交流（研究室メンバー間の議論や後輩指導）のチャンスが多いことや，様々な挑戦的研究テーマにチャレンジできることなど，メリットを活かす運営・活動を心掛けています．

　研究室内の活動として，週一で全体ミーティング，グループミーティング，輪講，学生主体の勉強会を毎週行い，年間3～4回／人の中間発表を実施しています．グループとは研究テーマ別に3～6名×5班に分けたもので，各グループ内で議論・情報共有・勉強会・後輩指導を密に行って切磋琢磨しています．研究課題は学生一人一人に与えており，基本的に先輩後輩関係なく独立して学位論文を書き上げていきますが，学生にはたとえ同期や後輩でも相談（and 雑談）できる相手が身近にいることが大事であり，ひいては研究遂行の促進にもなります．まさに大所帯研究室のメリットでもあります．ところで，当研究室は計算系のため解析自体がほぼ遠隔で行えるので，コロナ禍による支障は僅か．．．と当初は思っていました．しかし，学生間の些細な雑談（をきっかけにした大事な議論）が生まれにくく，全てリモートの研究活動ではボディブローのように悪影響が出てきたように感じます．研究遂行は個人プレーでも，仲間（peer）達が隣に座っている環境こそが“研究室”として大事な存在価値である，としみじみ思います．

産学連携の取り組み

　当研究室では，次節に紹介する基礎研究のみならず産学共同研究や技術相談にて，溶液の微粒化過程や微小液滴の飛散現象，ガス流の層流／乱流均質化，物質漏洩源推定など，産業現場で直面している複雑流の現象解明に向けた解析を行って参りました．

　当研究室も参画する東京理科大学ウォーターフロンティア研究センター（W-FSTセンター）⁽¹⁾では，物理・化学・材料・機械など幅広い分野の専門家を結集して「材料表面・界面における水の学際研究拠点」を形成し，分子から流体スケールに及ぶ材料表面・界面における水の新しい学理の創成とその工学的応用を目指した活動をしております．そもそも材料表面・界面に存在する水の吸着・濡れ・流れといった挙動は，表面の親水・撥水性や摩擦特性等の材料機能の発現を決定付けていますが，材料表面における水の挙動は原子・分子スケールの物理・化学状態や，ナノからマイクロスケールの凹凸形状等により複雑に変化します．一方，メートルオーダのバルク水挙動は乱流状態にあっても，ミクロな壁面性状・形状がマクロな乱流と相互影響します．そこから生じる現象や問題に対して，スケールの階層もしくは分野の垣根を超えた新しい水（流体）の学理に根差した研究センターです．企業から研究相談を頂くと，学内の複数異分野研究者が参画し，多面的に問題解決に取り組めるというのがW-FSTセンターの特徴ですので，お気軽にご相談いただければ幸いです．

主な研究テーマ

１．亜臨界乱流遷移

　現代の“ものづくり”において，試験機作成前にCFD解析から設計指針を立て，機器形状や運転条件の最適化をある程度まで図ることが一般的となっています．今後も益々，デジタルツインでCFD解析の担う場面は増えますが，依然として予測困難な現象の一つが「層流—乱流の亜臨界遷移」です．その解明を目標に，当研究室では乱流モデルを用いない直接数値シミュレーション（DNS: direct numerical simulation）により解析を進めています．釈迦に説法かもしれませんが，流れの状態は大別して層流と乱流があり，前者は流れの時空間的変化が規則的または緩やかなため予測も比較的容易であり，後者は運動量・熱・物質の混合が活発なため壁面摩擦・熱伝達・物質拡散が層流に比べて格段に促進されます．流れが層流と乱流のいずれであるかを予測し，乱流伝熱量などを正確に見積もることが工学的に重要です．実際，当研究テーマは冷却材循環系の安全性評価や，航空機翼面の遷移点予測に端を発します．

　流体力学の教科書では，円管内流れの臨界レイノルズ数（一解釈として“層流⇔乱流が切り替わる無次元流速の閾値”）は2000や2300と記されていますが，これは飽くまでも経験則であり，数学的または力学的な裏付けが困難でした．流動形態（例えば平行平板間や境界層）が異なれば，臨界レイノルズ数も遷移過程も有意に変わりますので，普遍則も見出したいところです．1883年のOsborne Reynoldsの先駆的実験から一世紀以上を過ぎた最近，局在乱流（円管内流れのパフなど）や大規模な層流—乱流共存パターン（平行平板間の乱流縞など）が臨界現象を特徴づけるキー構造として注目されています．例えば，パフの寿命と分裂の兼ね合いから臨界レイノルズ数が2040 ± 10と定められました⁽²⁾．さらには，パフや縞の確率的分裂減衰挙動と有向浸透現象（DP: directed percolation）との関連が議論され，1986 年の Yves Pomeau によるDP 普遍性の予言⁽³⁾が実証されつつあります．当研究室でも，図1のような多様な層流—乱流共存パターンおよびDP普遍性を様々な流動形態について調査を進めており，ダクト流⁽⁴⁾，環状流⁽⁵⁾や仮想拡張流路（空間的制約を緩和）⁽⁶⁾においてDP普遍クラスとしての特徴（時には擬DP）を発見しています．つまり，流体現象がNavier–Stokes方程式による決定論的でありながら，確率論的解釈の可能性を示唆していることが興味深いところです．

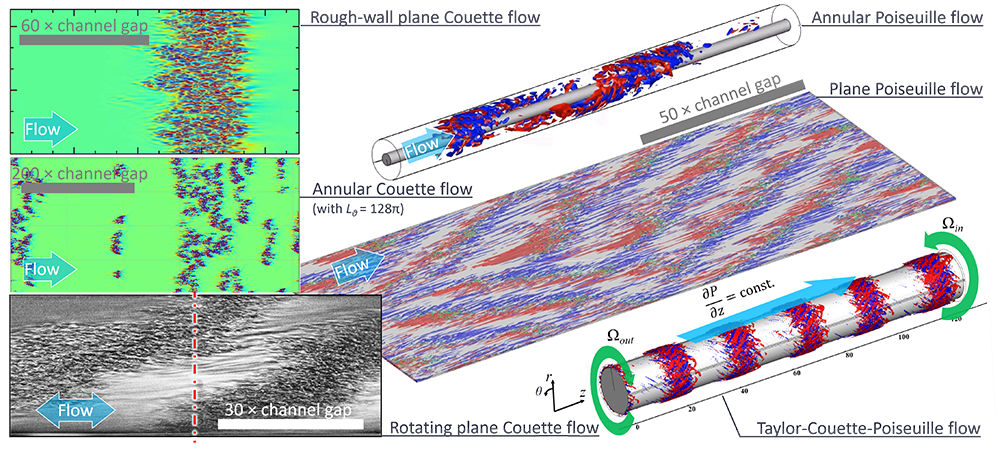
図1　層流―乱流共存パターン形成．カラーコンターおよび等値面（赤・青）は速度変動を可視化しており，緑や等値面不在は準層流域に相当．速度変動の密集した局在乱流帯が，チャネル幅の数十倍以上の間隔でパターン形成を呈している．右下図から反時計回りに，テイラー・クエット・ポアズイユ流⁽⁷⁾，平面ポアズイユ流⁽⁸⁾，環状ポアズイユ流⁽⁹⁾，片壁粗面平面クエット流⁽¹⁰⁾，仮想流路拡張した環状クエット流⁽⁶⁾，回転平面クエット流（フレーク状粒子の可視化結果）⁽¹¹⁾．

　動画1のように，高アスペクト比の矩形断面流路を流れるダクト流でも，局在乱流が側壁に衝突しながらも，時折，反射するように斜め方向へ伸びたり，分裂したりを繰り返し，時空間欠性を半永久的に維持します．これが，乱流維持限界の臨界状態の一例です．また，伝熱特性に与える影響も調査し，局在乱流パターン形成が有意な伝熱促進または非相似性をもたらすことを見出しました⁽¹²⁾．ご関心あれば，解説記事⁽¹³⁾をご覧ください．

動画1　アスペクト比48のダクト流における局在乱流パターンの時間変化⁽⁴⁾．主流(x)方向に周期境界を課した計算領域のサイズはL_x×L_y×L_z = 256×1×48で，コンターはy方向中央断面全域におけるy方向速度を可視化（赤と青は正負を示し，緑は準層流域に相当）しているが，パターンの見易さのためバルク平均速度で可視化フレームは定速移動させている．

 

　宇宙航空研究開発機構（JAXA）・石田貴大氏，芝浦工業大学・河田卓也准教授との共同で，後退平板境界層における乱流遷移の研究を行っております．詳細は省きますが，DNSに加えて非線形放物型安定方程式（NPSE）や風洞試験より，翼粗面や主流乱れが及ぼす横流れ不安定の乱流遷移過程への影響（遅延／促進）を研究しています^(14-17)．図2は研究対象とDNS結果の一部です（あくまでイメージのために，各図の寸法は一致させていません）．

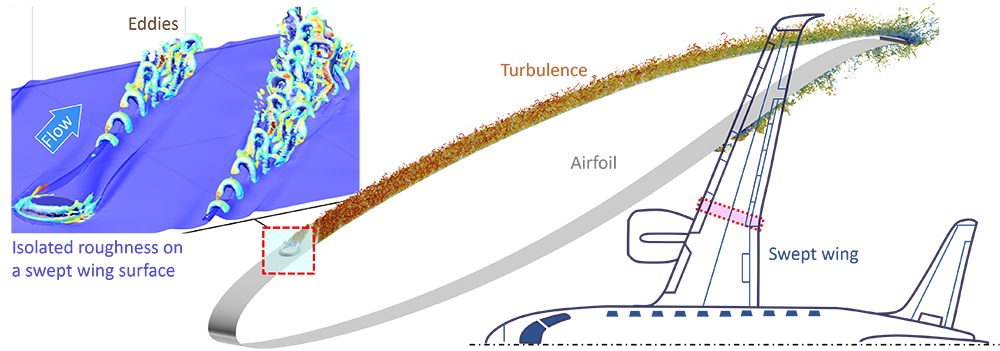
図2　後退翼面上の孤立粗度が促進させる乱流遷移．JAXA共同研究．

２．弾性慣性乱流

　ポリマーや界面活性剤の希薄水溶液は弾性的性質を持つ流体となり，条件が整えば高レイノルズ数での乱流摩擦抵抗がニュートン流体の場合に比べて大きく低減されます．これはトムズ効果とも呼ばれ，パイプライン流体輸送におけるポンプ動力節約など，省エネルギ化に貢献できる流体工学技術です．また一方，低いレイノルズ数では層流にならずに特異な変動場，いわゆる弾性慣性乱流（EIT: elasto-inertial turbulence）を呈し，マイクロ流路での混合促進にも応用が期待されます．しかし，これらトムズ効果とEITをもたらすメカニズムは未解明であり，さらには複雑流路における流動特性の予測には課題が残ります．

　そこで，層流状態でありながら定性的に異なる渦群を任意に選択可能な流れ場（回転平面クエット流⁽¹¹⁾）を対象にすることで，粘弾性流体乱流中で起きえる渦の変調・抑制・促進，または粘弾性誘起の流れ不安定性を系統的に調査しています（図3）．DNS等で粘弾性由来の様々な特徴や現象を発見し，丹念な系統的調査を通してトムズ効果とEITの更なる解明をしてきました．その成果^(18-20)により，仁村友洋氏（現・東京農工大学特任助教）が博士号を取得されました．

図3　回転平面クエット流における縦渦の蛇行（左図）が，流体の粘弾性によって抑制されて直線的な二次元定常渦になる様子（中央）⁽¹⁸⁾．より低いレイノルズ数では，粘弾性誘起のスパン方向渦が支配的となるEITが発生（右）⁽²⁰⁾．渦の可視化は，速度勾配テンソル第二不変量Qによる．

３．界面張力差対流

　最先端ものづくりの場面において，多孔質体や繊維束などの狭隘空間を流路とした液体流れは数多く，またはLab-on-a-Chipなどのマイクロ流路における細胞・薬品操作を必要とする産業場面も増えています．それらのマイクロ流動現象における液滴・気泡・粒子の挙動予測や制御は製品性能の高度化に繋がります．マイクロ流れの流体運動において支配的な要素は界面張力と濡れ性であり，これらの制御によりマイクロスケールでのバルク流の効率的輸送，伝熱特性の効率化などが望めます．近年，固気液界面を有するマイクロ流動現象についても，（乱流を対象としていないが）DNSが行われるようになり，実験では測定し難い3次元速度測定や界面張力測定が可能となりました．

　当研究室では学内プロジェクトとして，DNSを用いた界面張力駆動流現象の解明を目的に，元祐昌廣教授と共同で「マイクロ液滴の光熱マニピュレーションに関わる熱流動⁽²¹⁾」，「光異性化界面活性剤水溶液の液注駆動⁽²²⁾」，「局所加熱蒸気泡における粒子集積現象⁽²³⁾」，また上野一郎教授と共同で「動的濡れの自発的『メニスカス・クリーニング』機構⁽²⁴⁾」「温度差マランゴニ対流を伴う2自由界面液膜の基本流⁽²⁵⁾」の解析が進められてきました（動画2）．いずれの数値計算もオープンCFDツールのOpenFOAM®をプラットフォームに，Volume of Fluid法で移動界面の追跡を実現し，その界面がもたらすラプラス圧とマランゴニ効果を考慮しています．

動画2　自由界面を有するμm～mmスケール熱・流体現象の数値シミュレーション例．左上図は，UV照射で異性化する界面活性剤水溶液を模擬した液注駆動の再現⁽²²⁾．左下から右図に向かって，局所加熱蒸気泡周りの流線⁽²³⁾，温度差マランゴニ効果による液滴駆動⁽²¹⁾，矩形枠内の自由液膜における温度差マランゴニ対流の基本流⁽²⁵⁾，比重の大きい剛体球の水界面トラップの再現．

４．ステント留置した冠動脈分岐部の血流

　冠動脈血管の狭窄による虚血性心疾患は世界的にも死因第一位であり，その治療法にバルーンとステントで狭窄血管を押し広げる経皮的冠動脈インターベンション（PCI）治療があります．ステント自体の技術向上もあり，冠動脈直管部（非分岐部）に対する治療成績は十分に高くなってきています．それに比べて，分岐部病変に対するステント留置術の治療成績は低くく，様々な手技の有効性についての議論が続いています．元来，ステントは一本の筒状であり，分岐部に留置すると側枝または本幹の入口を塞ぐ（jail）ことになり，jailされた側の血流が滞ることは容易に予測できます．そのため，分岐部留置したステントに対してバルーンで側枝入口付近を空けるようにステントストラットを変形させるKBT（kissing balloon technique）や，複数ステントを留置する手技（Crush/Culotte/T-stenting等）が提案されてきました．非分岐部に対する治療と比較して，血流の血管壁に与える力学的刺激等，病変促進に関係する要因も多くあることは知られていますが，冠動脈分岐部ステント治療が具体的にどのように病変に関わるか未だ明らかにされていません．血流変化は病変促進に深く関わりますが，患者から実際に測定することは極めて困難であり，数値流体解析で血流を知ることはPCI治療成績の向上には大変有益です．

　上記の背景の下，分岐血管においてステント留置した血行状態変化の解明を目的として，ステント留置の構造解析およびCFD解析を行っています^(26,27)．動画3はCulotte stentingの再現シミュレーションで，さらにKBTの有無による血流変化（特に血管およびステントに及ぼすWSS）を調べたものです．当研究は，柏厚生総合病院循環器内科・藤野祐介医師との共同プロジェクトです．

動画3　左冠動脈分岐モデルへの2ステント留置（Culotte stenting）の構造解析シミュレーション（左図），およびCFDシミュレーションによる壁面せん断応力（wall shear stress: WSS）分布結果⁽²⁷⁾．留置したステントのストラット表面が高いWSSになっている様子が確認できる．

５．流体力学×機械学習

　従来，統計的特徴に基づいて壁乱流の本質理解や状態予測は行われてきましたが，いま，機械学習の援用により瞬時場から有意な特徴量抽出の可能性を議論できる時代となりました．例えばチャネル乱流は，瞬時・局所に捉えれば乱流生成・拡散・散逸が間欠的に生じる非平衡状態にあり，一見して無秩序に千差万別な乱れと渦にも有意な特徴を含有していると考えました．統計処理によって均される（失われる）瞬時場独自の特徴が抽出できれば，時空間的に限られた情報から内部（内在する物理）や外部（初期条件・境界条件）を予測することも可能と期待できます．チャネル乱流の直接数値計算（DNS）などにより必然的に時々刻々と瞬時場データは蓄積され，膨大な乱流ビッグデータを活用しやすい環境（時代）となった今，改めて人工ニューラルネットワークによる深層学習の可能性を追究します（図4）． ご関心あれば，解説記事⁽²⁸⁾をご覧ください．

図4　乱流ビッグデータに基づく内在物理や外部条件の推論．記事⁽²⁸⁾から再掲．

　2021年度からは科研費基盤研究(S)「機械学習を活用した革新的流れ制御パラダイムの創出と実践」（代表：慶應義塾大学・深潟康二教授）のもと，機械学習を用いた流れ制御・予測の研究を行っています⁽²⁹⁾．特に本研究室では場の推定を目指しており，速度場⇔温度場の推定，速度場⇒構成応力場の推定，局所濃度場⇒拡散源の推定について研究しています．また，東京大学生産技術研究所・長谷川洋介教授と共同で，群知能センサーロボットによる拡散源推定⁽³⁰⁾などにも挑戦中です．

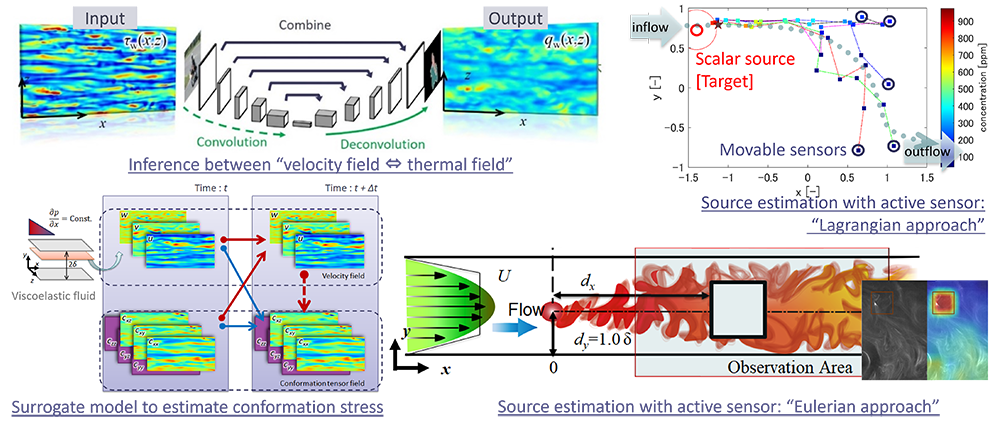
図5　機械学習や群知能を応用した乱流中の各種“場”の推定．

謝辞

　本研究の一部は科学研究費補助金（16H06066，16H00813，18H03758，19H02071，20KK0085，21H05007：分担含む）の助成により行われました．また，計算の一部は東北大学サイバーサイエンスセンターおよび大阪大学サイバーメディアセンターのスーパーコンピュータにより行われました．

参考文献

(1)	東京理科大学ウォーターフロンティア研究センター（WaTUS）．https://www.rs.tus.ac.jp/watus/jp/
(2)	K. Avila, D. Moxey, A. de Lozar, M. Avila, D. Barkley, & B. Hof (2011) “The onset of turbulence in pipe flow,” Science 333, 192–196.
(3)	Y. Pomeau (1986) “Front motion, metastability and subcritical bifurcations in hydrodynamics,” Physica D 23, 3–11.
(4)	K. Kohyama, M. Sano, & T. Tsukahara (2022) “Sidewall effect on turbulent band in subcritical transition of high-aspect-ratio duct flow,” Phys. Fluids 34, 084112.
(5)	K. Kunii, T. Ishida, Y. Duguet, & T. Tsukahara (2019) “Laminar-turbulent coexistence in annular Couette flow,” J. Fluid Mech. 879, 579–603.
(6)	K. Takeda, Y. Duguet, & T. Tsukahara (2020) “Intermittency and critical scaling in annular Couette flow,” Entropy 22, 988.
(7)	Y. Matsukawa & T. Tsukahara (2022) “Subcritical transition of Taylor-Couette-Poiseuille flow at high radius ratio,” Physics of Fluids 34, 074109.
(8)	塚原隆裕，石田貴大 (2015) “平面ポアズイユ流の亜臨界遷移における下臨界レイノルズ数”，日本流体力学会誌「ながれ」34(6)，383-386.
(9)	T. Ishida, Y. Duguet, & T. Tsukahara (2016) “Transitional structures in annular Poiseuille flow depending on radius ratio,” J. Fluid Mech. 794, R2.
(10)	T. Tsukahara, T. Tomioka, T. Ishida, Y. Duguet, & G. Brethouwer (2018) “Transverse turbulent bands in rough plane Couette flow,” J. Fluid Sci. & Tech. 13(3), JFST0019.
(11)	T. Tsukahara, N. Tillmark, & P.H. Alfredsson (2010) “Flow regimes in a plane Couette flow with system rotation,” J. Fluid Mech. 648, 5–33.
(12)	T. Fukuda & T. Tsukahara (2020) “Heat transfer of transitional regime with helical turbulence in annular flow,” Int. J. Heat & Fluid Flow 82, 108555.
(13)	塚原隆裕，福留功二 (2022) “亜臨界遷移の“局在乱流”熱伝達”，日本伝熱学会誌「伝熱」61(257)，pp. 50–56.
(14)	T. Ishida, T. Tsukahara, & N. Tokugawa (2022) “Parameter effects of spanwise-arrayed cylindrical roughness elements on transition in the Falkner-Skan-Cooke boundary layer,” Trans. Japan Soc. Aeronautical & Space Sci. 65, 84–94.
(15)	T. Ishida, K. Ohira, R. Hosoi, N. Tokugawa, & T. Tsukahara (2022) “Numerical and experimental analysis of three-dimensional boundary-layer transition induced by isolated cylindrical roughness elements,” Int. J. Aeronautical & Space Sci. 23, 649–659.
(16)	K. Nakagawa, T. Tsukahara, & T. Ishida (2023) “DNS study on turbulent transition induced by an interaction between freestream turbulence and cylindrical roughness in swept flat-plate boundary layer,” Aerospace 10, 128.
(17)	K. Nakagawa, T. Ishida, & T. Tsukahara (2023) “Effects of freestream turbulence on the secondary instability of the roughness-induced crossflow vortex in swept flat plate boundary layers,” Int. J. Heat & Fluid Flow 102, 109161.
(18)	T. Nimura, T. Kawata, & T. Tsukahara (2018) “Viscoelastic effect on steady wavy roll cells in wall-bounded shear flow,” Fluid Dyn. Res. 50, 051414.
(19)	T. Nimura, T. Kawata, & T. Tsukahara (2018) “Viscoelasticity-induced pulsatile motion of 2D roll cell in laminar wall-bounded shear flow,” Int. J. Heat & Fluid Flow 74, 65–75.
(20)	T. Nimura & T. Tsukahara (2022) “Viscoelasticity-induced instability in plane Couette flow at very low Reynolds number,” Fluids 7, 241.
(21)	N. Kazuno, T. Tsukahara, & M. Motosuke (2017) “Laplace pressure versus Marangoni convection in photothermal manipulation of micro droplet,” Euro. Phys. J. SP 226, 1337–1348.
(22)	K. Nitta & T. Tsukahara (2018) “Numerical demonstration of in-tube liquid-column migration driven by photoisomerization,” Micromachines 9, 533.
(23)	S. Fujimura, K. Yamamoto, M. Motosuke, & T. Tsukahara (2020) “Numerical study of thermocapillary-driven flow of a micro bubble on locally heated wall,” Heat Transfer Res. 51, 1087–1104.
(24)	H. Nakamura, T. Ogawa, M. Inoue, T. Hori, L. Mu, H. N. Yoshikawa, F. Zoueshtiagh, G. F. Dietze, T. Tsukahara, & I. Ueno (2020) “Enhancement of meniscus pump by multiple particles,” Langmuir 36, 4447–4453.
(25)	T. Homma, T. Yamashita, R. Wada, K. Kawazu, K. Kurose, T. Tsukahara, & I. Ueno (2023) “Multicellular structures in thin free liquid films induced by thermocapillary effect,” J. Colloid & Interface Sci. 641, 187–196.
(26)	Y. Fujino et al. (2017) “Difference in vascular response between sirolimus-eluting- and everolimus-eluting stents in ostial left circumflex artery after unprotected left main as observed by optical coherence tomography,” Int. J. Cardiology 230, 284–292.
(27)	大屋 慶季，藤野 祐介，塚原 隆裕 (2022)，“数値流体解析による血管分岐部におけるステントストラット非圧着距離が血流に与える影響調査”，第59回日本心血管インターベンション治療学会 関東甲信越地方会，東京.
(28)	慶應義塾大学 理工学部 機械工学科 深潟研究室，機械学習のページ．https://kflab.jp/ja/?21H05007
(29)	塚原隆裕 (2022) ”粘弾性流体や乱流拡散を対象とした深層学習”，日本機械学会流体工学部門ニュースレター「流れ」，2022年11月号．https://www.jsme-fed.org/newsletters/2022_11/no5.html
(30)	大西諒・他 (2023) “非一様流における移動センサを用いたスカラー源探査手法に関する研究”，第38回生研TSFDシンポジウム，東京．