様々な加速度環境における自由表面流の数値解析⁽¹⁾
（CIP法，MARS法，Level Set法を協調した解法の改良）

姫野 武洋*1 東京大学 大学院工学系研究科 航空宇宙工学専攻

Numerical Analysis of Free-surface Flows under Various Conditions in Acceleration (Improvement of CIP-LSM : CIP-based Level Set & MARS) Takehiro HIMENO*1 *1 University of Tokyo, Department of Aeronautics and Astronautics

1.　はじめに

　人類の活動領域が地球周回軌道上まで拡大するのに伴い，液体ロケットや人工衛星の推進薬タンクやエンジン，宇宙ステーションでの熱制御装置など，地上とは異なる加速度環境で液体を利用する場面が増えつつある．このような環境では，貯蔵容器内の液体を望ましい位置に保持し，思い通りに外部へ搬送するなど，自由表面流を管理することが非常に難しい．特に，地上から地球周回軌道まで機体姿勢やエンジン推力を変えながら飛行する液体ロケットや，比重差を利用した流体の駆動と安定化を期待できない微小重力環境で長期間に亘り作動する人工衛星について，開発コストと運用リスクを低減させるためには，その設計段階からタンクや配管内部における推進薬の挙動を適切に予測することが重要である．このように特殊な加速度環境における自由表面流の挙動予測と制御は，宇宙工学の分野で，”流体管理(fluid management)”，あるいは，宇宙輸送システムに限って，”推進薬管理(propellant management)”と呼ばれる⁽²⁾⁽³⁾．これら推進薬管理に関する技術課題を解決するためには，地上では再現が困難な熱流動現象に関する知見の獲得と蓄積が不可欠であり，理論と実験を補完する手段として数値解析手法の確立が期待されている．

 

2.　自由表面流の数値解析手法

　このような動機付けから，東京大学と宇宙航空研究開発機構(JAXA)は協力して，様々な加速度環境における自由表面流を予測する数値的手法として，CIP法⁽⁴⁾，MARS法⁽⁵⁾，Level Set法⁽⁶⁾を協調的に組み合わせたCIP-LSM (CIP-based Level Set & MARS) ⁽⁷⁾⁽⁸⁾を提案して改良を続けてきた。並行して、落下塔や加振機を用いて実現される微小重力環境や動的加速度環境における気液界面観察実験^(9)(10)を実施し，対応する数値解との比較により，同手法の妥当性検証にも取り組んでいる．数値解析手法の支配方程式や離散化手法については論文本編⁽¹⁾，に詳しく述べているので，ここでは解法のうち界面捕獲法の考え方を簡単に説明したい．

　界面捕獲法として採用したMARS法は、PLIC-VOF法の一種であり、二値関数の有限体積的な移流に優れている。図1に示すように、検査体積(計算セル)内部における気液存在割合(VOF関数)の分布を区分的1次関数により内挿補間し、台形積分によって流束を推定するため、VOF関数の数値的散逸を本質的に回避でき、界面を横切る物性値の跳びを1 格子幅以内で捕獲することができる。加えて、図2に示すように、独立変数であるVOF関数を用いて捕獲される気液界面に、従属変数としてLevel Set関数(距離関数)を重畳することで、法線ベクトルや曲率など、気液界面形状に関する情報を高精度に獲得し、界面張力の高精度な評価を可能にしている。

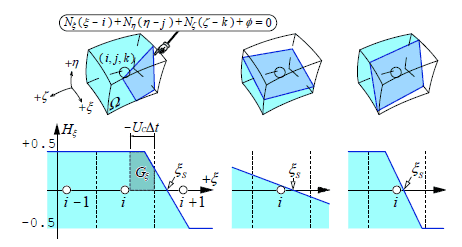
図1 : MARS法 : 区分的1次関数を用いた面積分率の内挿補間と体積分率の流束算出

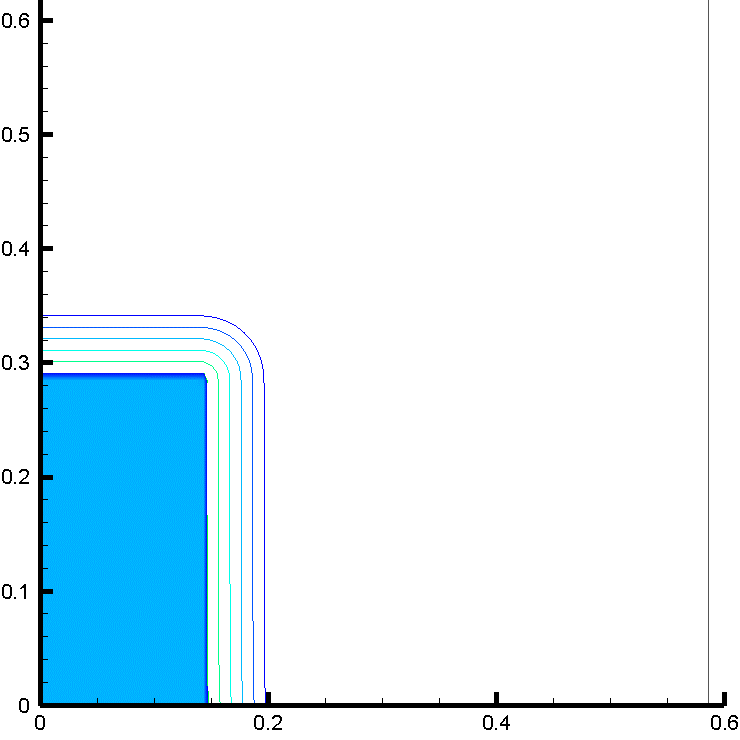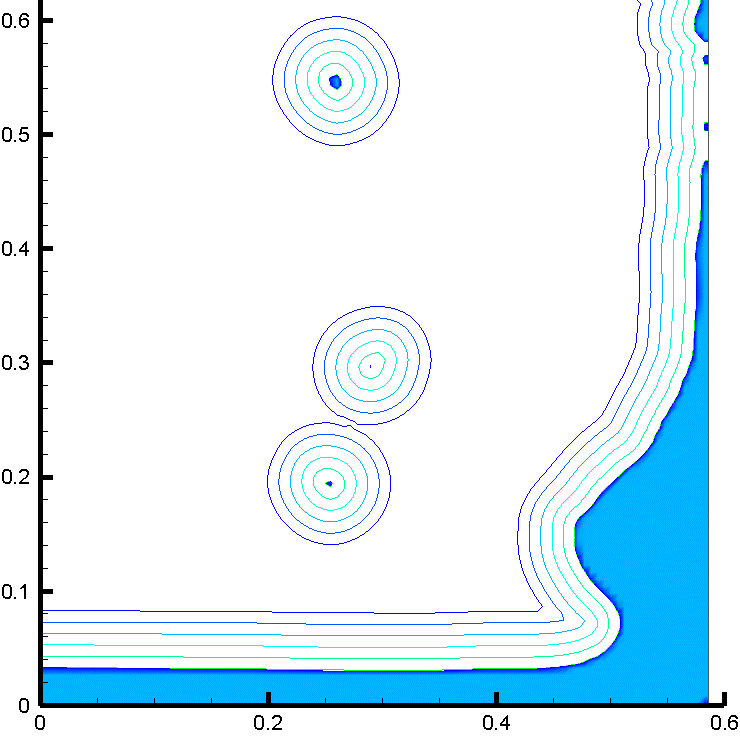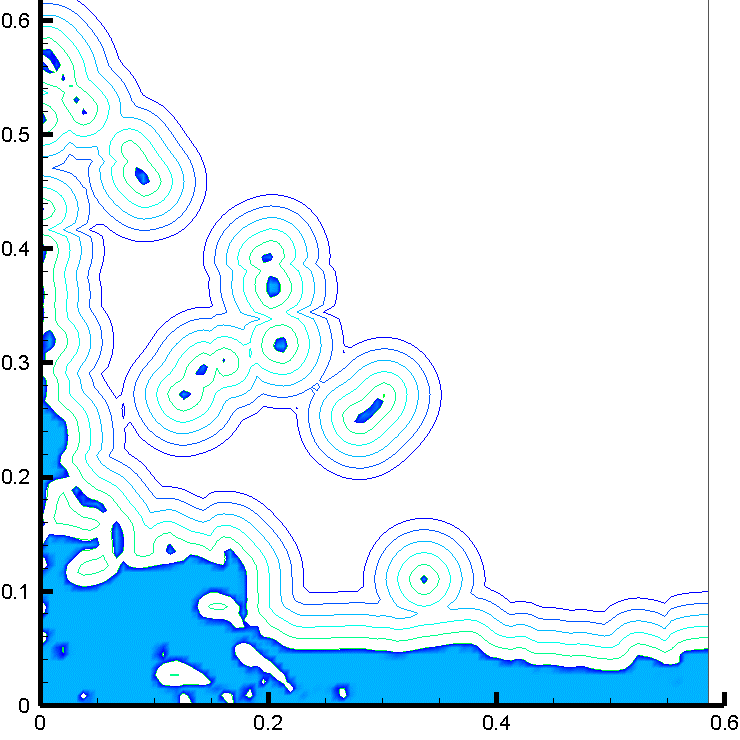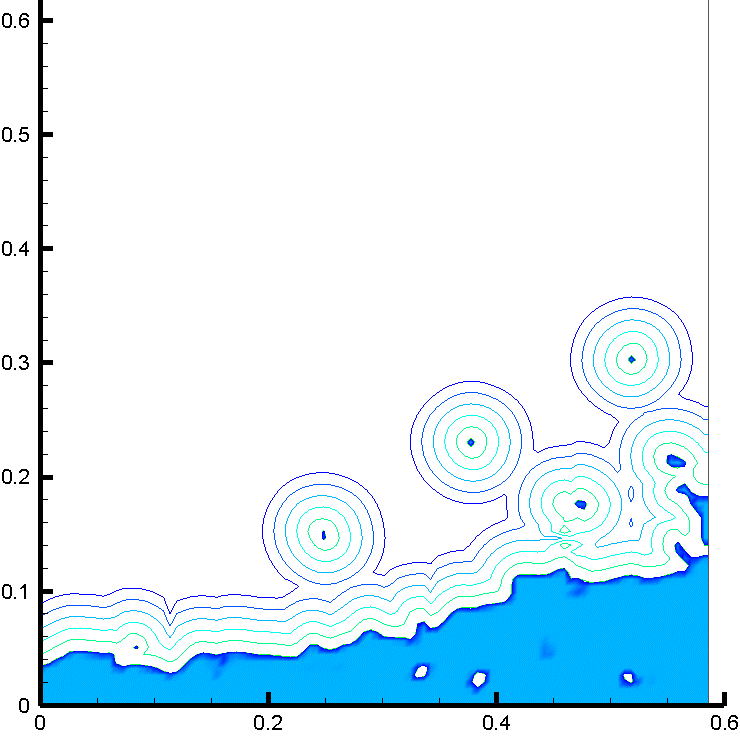
図2 : CIP-LSMにおける界面捕獲 : MARS法で捕獲された界面に時事刻々重畳される距離関数

 

3.　自由表面流の挙動に関する解析事例

　数値解析手法の適用性と妥当性を評価するために、静的あるいは動的な加速度を受けて気液間の比重差に駆動される流れと，ほぼ無重量の環境で界面張力と濡れ性に駆動される流れについて，それぞれ数値的模擬を試みた。WEB上で閲覧される特長を活かし、以下では動画を交えながら、それぞれの解析結果等を紹介する。

3・1　静的加速度環境 (ダム崩壊問題)

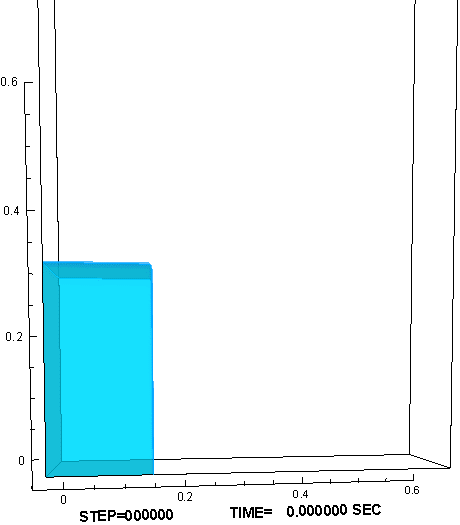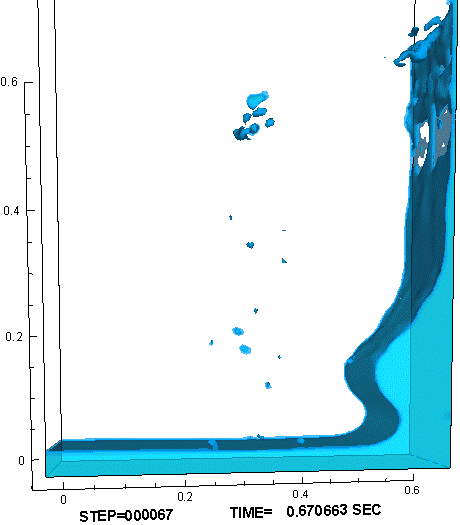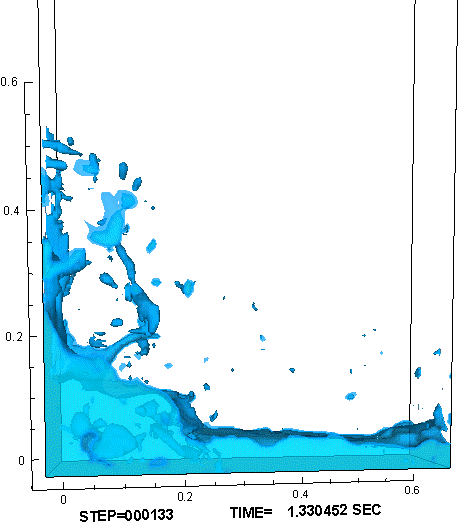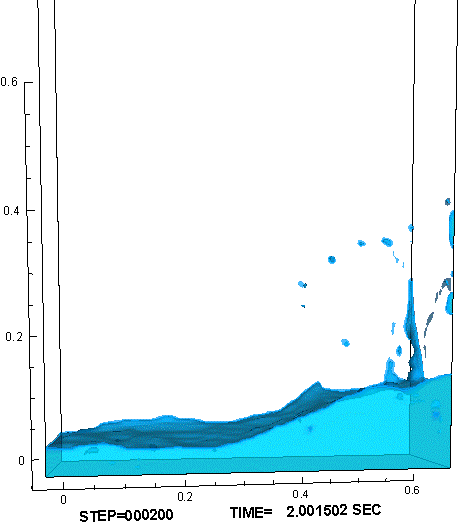
　時間的に一定の重力が加わる環境に置かれ，気体と液体の比重差に駆動されて液面が大変形する例として、水槽内部でのダム崩壊実験⁽¹¹⁾を参照し、対応する数値解析を行った。計算では、作動流体として、非圧縮流体である水と理想気体の状態方程式に従う空気を用いた。図3に示すように、水槽底面を走る水際線の位置、右壁に衝突して鉛直方向に立ち上る水柱の形状、砕波しながら再崩壊する水柱に空気が飲み込まれる様子、水槽底面で跳躍した波頭が再び左壁に到達する様子など、対応する実験で観察された液面形状の特徴的な変化が、計算でもよく再現できた。

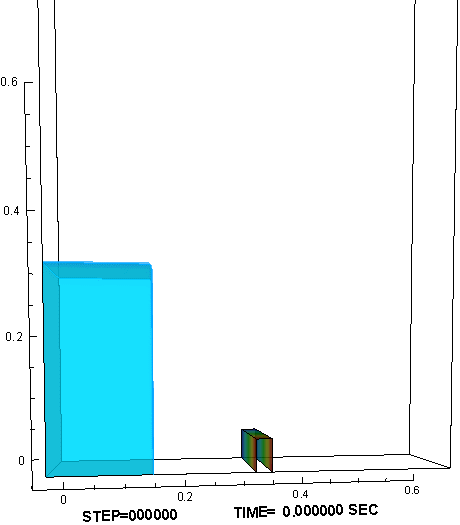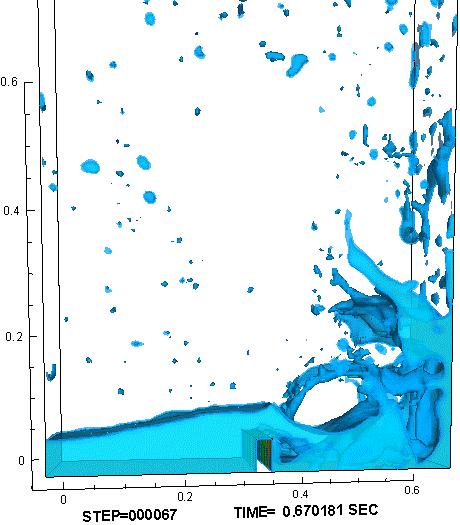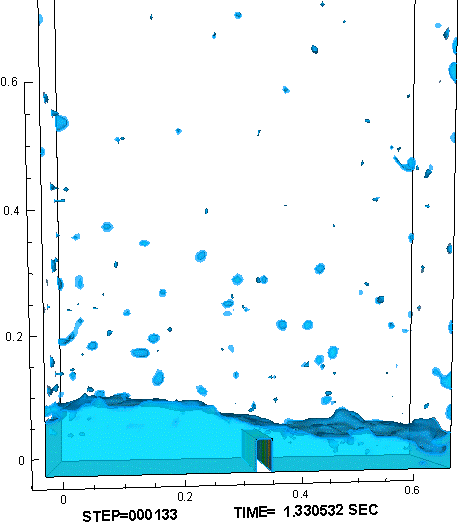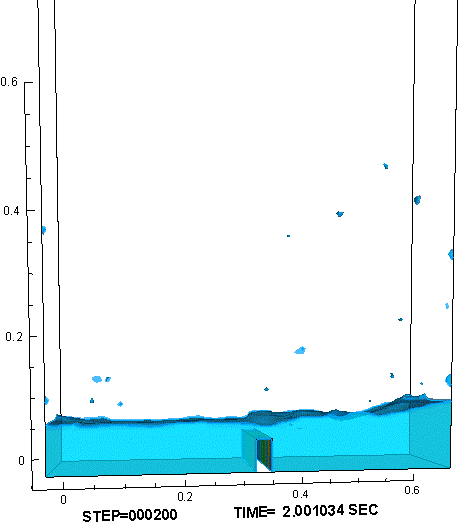図3 : ダム崩壊問題の数値解析結果。障害物が無い場合(左) と 有る場合(右)

3・2　非定常加速度 (再使用型液体ロケット推進薬タンクでのスロッシング)

　JAXA宇宙科学研究所では，再使用可能な液体ロケットの実現へ向け，図4のような，液体酸素と液体水素を推進薬とする圧力供給方式の小型エンジンを搭載したロケット実験機を用い，比較的短秒時の垂直離着陸飛行を反復する試験⁽¹²⁾に取り組んでいる．従来型の液体ロケットに比べ、再使用型の場合、地上帰還時の大気圏内飛行など、多様な飛行経路や機体姿勢を要求される。

　そのため、推進薬管理の視点からは、タンク内の液体推進薬が時間的に変化する加速度を受けて大きく揺動すること(スロッシング)が懸念される。大規模なスロッシングの発生は、機体の姿勢制御に有害なだけでなく、タンク吸引口から加圧ガスが排出されれば、ターボポンプの過回転や燃焼室での失火を誘発する危険性があるなど、エンジンにとっても有害である。スロッシングを抑制するためには、タンク内に邪魔板などの減衰器具を艤装すべきであるが、飛行中の加速度環境を地上で再現するのは難しく、スロッシングの規模や減衰器具の効果を事前評価するのは容易でない。

　そこで筆者らは、図5に示すような水平方向加振機に実機タンクの縮小模型を搭載した地上実験を行うとともに、対応する三次元数値解析を試みた。

図4 :ロケット実験機の垂直離着陸試験	図5 : スロッシング実験装置

　図6に示すのは、上下ドームを有する円筒小容器を加振し、砕波を伴うスロッシングを高速度カメラにより観察した実験結果と、三次元物体適合格子を用いて行った数値解析結果である。気液界面の変形に注目すると、波頭形状、液体がタンク頂部へ達する様子、それ以降の砕波現象など、対応する実験結果が計算でも良く再現されているのが分かる。その一方、格子スケール以下の液滴や気泡を界面捕獲法で捉えられないことも明らかであることから、計算対象に応じた格子密度の設定が重要であることも確認できる。

図6 : 模型タンク内のスロッシング観察結果(左)と対応する数値解析 (右)

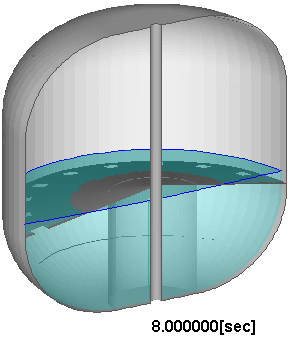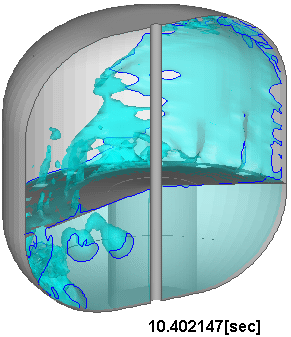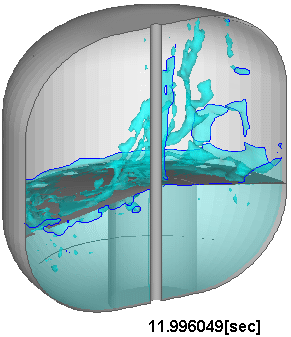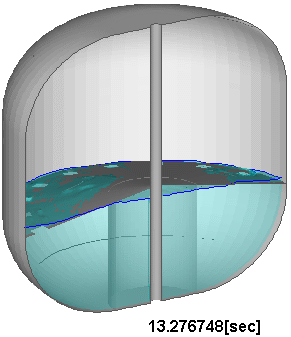
　検証計算によって数値解に対する一定の妥当性が確認されたのを受け、図7に示すように、実験機の飛行条件により近い加速度条件を課した場合や、スロッシング抑制のための邪魔板をタンク内部に装備した場合についても数値的模擬を試み、対応する実験との比較を通じて、計算の妥当性を確認している。

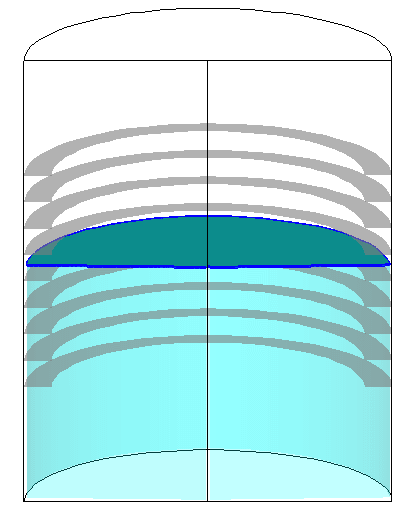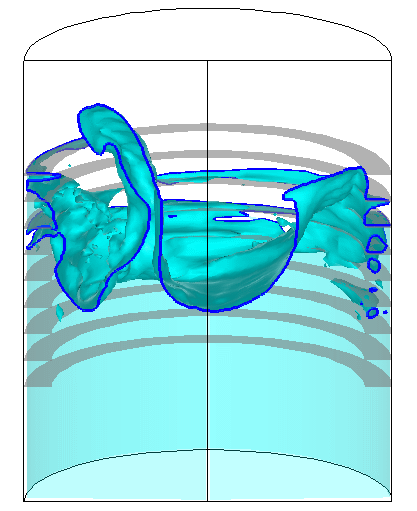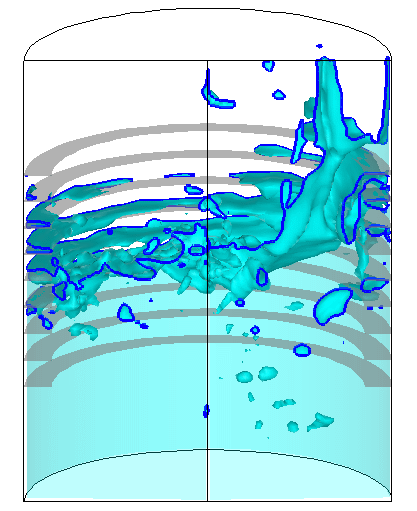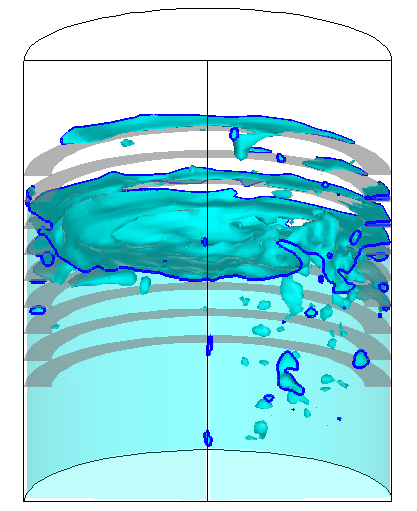図7 : 邪魔板を有する推進薬タンク内のスロッシング解析

3・3　低重力環境

　最後に，微小重力環境に置かれた円筒容器の内部で，界面張力と濡れ性に駆動されて変形する界面について，落下塔実験と数値的模擬を行った結果の一例を示す．図8に示すように、実験では高さ約10 mの落下塔を用い、1/1000G以下の加速度環境を落下筐体内部で約1秒間にわたって実現した。一連の落下塔実験では，界面張力によって駆動される自由表面流の非定常現象について基礎的な知見を獲得するとともに，初期条件と境界条件が明確に課された円筒容器内部の流れ場を観察することで，数値解法の検証に適したデータの蓄積を目的としている．

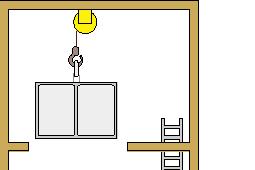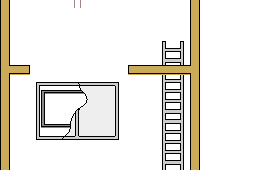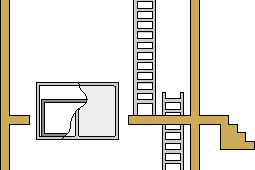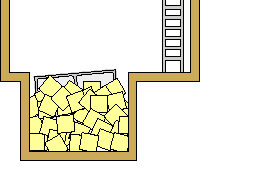図8 : 落下塔外観と落下筐体模式図 (東京大学、津江・中谷研究室より借用)

　図9に実験結果の一例(左)と共に、対応する数値解析結果(右)を示す。実験結果からは、微小重力環境で、固体壁面上の接触角を保とうとする濡れ性の効果と、液面の曲率を緩和しようとする 界面張力の効果によって液面形状が変化するのが分かる。また、落下開始の約1秒後に、落下筐体内部で、円筒容器を搭載した内箱が風除けの外箱に追突すると、液体の柱が立ち上る様子も観察された。計算結果が示す液面変形は、実験とよく一致していることから，界面厚を排除した今回の計算でも，界面張力波の伝播とそれに伴う界面変形を安定かつ精度良く模擬できると評価された．

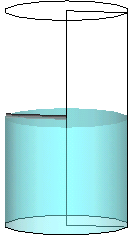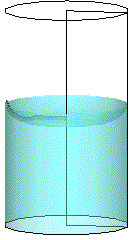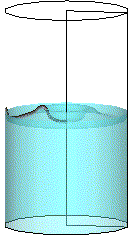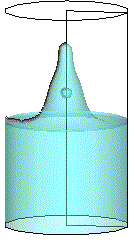図9 : 円筒内の表面張力駆動流、観察結果(左)と対応する数値解析 (右)

 

4.　おわりに

　様々な加速度環境における気液二相流動予測技術の確立へ向け、自由表面流解法 (CIP-LSM) の改良と、実験による知見の蓄積を通じた取り組みを紹介した。静的あるいは動的な加速度を受けて気液間の比重差に駆動される流れと、低重力環境で界面張力と濡れ性に駆動される流れについて、動的な液面変形に注目して計算結果と実験データを比較したところ、何れの場合でも、両者の間に良好な一致を確認できた。

　今後、直近の課題は、濡れ性モデルの高度化、乱流モデルの組み込み、相変化モデルの構築、および、混相流モデルとの融合であると認識している。これらの課題については、相変化を考慮した界面捕獲法⁽¹³⁾によるキャビテーション現象の数値解析(図10)⁽¹⁴⁾や、格子スケールより小さな液滴群のラグランジュ的な粒子追跡法と界面捕獲法を融合した微粒化現象の数値解析(図11)^(15)(16)などを通じて、新たな手法やモデルの妥当性評価を慎重に進めつつある。

図10 : 相変化を考慮した界面捕獲 によるキャビテーション現象の数値解析	図11 : 粒子追跡法と界面捕獲法のハイブリッド解法 による衝突微粒化現象の数値解析

　克服すべき課題は決して少なくないが，様々な環境に置かれた気液二相熱流動現象の理解に基づく各種機器の設計技術高度化に，本手法が役立てられることを期待したい．

 

References

(1)	T. Himeno, H. Negishi, S. Nonaka, C. Inoue, T. Watanabe and S. Uzawa, Numerical Analysis of Free-surface Flows under Various Conditions in Acceleration : Improvement of CIP-LSM : CIP-based Level Set & MARS, Trans. JSME Ser.B, Vol.76, No.765(2010), pp.778-788 (in Japanese)
(2)	Reynolds, W. C. and H. M. Statterlee, Liquid propellant behavior at low and zero g., The Dynamic Behavior of Liquids in Moving Containers, H. N. Abramson, (ed.), NASA SP-106 (1966), pp.387-449.
(3)	B. N. Antar and V. S. Nuotio-Antar, Fundamentals of Low Gravity Fluid Dynamics and Heat Transfer, (1993), CRC Press, ISBN 0-8493-8913-5.
(4)	T. Yabe and E. Takei, A new higher-order Godnov method for general hyperbolic equations, J. Phys. Soc. Japan, Vol.57 (1988), pp.2598-2601.
(5)	T. Kunugi, MARS for multiphase calculation, Computational Fluid Dynamics Journal, ,Vol.9, No.1(2000).
(6)	M. Sussman, P. Smereka, and S. Osher, A level set approach for computing solutions to incompressible two-phase flow, J. Comput. Phys., Vol.114 (1994), pp. 146-159
(7)	T. Himeno and T. Watanabe, Thermo-Fluid Management under Low-gravity Conditions : 2nd Report, Free-Surface Flows Driven by Surface Forces, Trans. JSME Ser.B, Vol.68, No.687(2003), pp.2400-2407 (in Japanese)
(8)	T. Himeno, S. Nonaka, Y. Naruo, Y. Inatani and T. Watanabe,“Numerical Analysis of Sloshing and Wave Breaking in a Small Vessel by CIP-LSM” , JSME International Journal, Series B, Vol.47, No.4(2004), pp.709-715.
(9)	T. Himeno, T. Watanabe and R. Imai, “Numerical Analysis of Free Surface Flows Driven by Interfacial Tension Effect”, Journal of the Japan Society of Microgravity Application, Vol.23, No.2(2006), pp.99-105.
(10)	T. Himeno, T. Watanabe, S.Nonaka, Y. Naruo,,Y.Inatani and H. Aoki, Numerical and Experimental Investigation on Sloshing in Rocket Tanks with Damping Devices, AIAA Paper 2007-5557(2007)
(11)	Koshizuka, S., Tamako, H., and Oka, Y, Computational Fluid Dynamics J. Vol. 4, (1995), pp.29-46.
(12)	Y. Inatani, Y. Naruo and K. Yonemoto, J. Spacecraft and Rockets, AIAA, Vol.38, No.1 (2001), pp.36-42
(13)	Y.Umemura, T. Himeno and T. Watanabe, Numerical Simulation of Bubble Growth and Departure on Heat Transfer Surface, J. Jpn. Soc. Microgravity Appl. Vol. 29 No.1 (2012), pp.2-7 (in Japanese).
(14)	K.Ishikawa, Y.Umemura, T. Himeno, T. Watanabe, N. Tani, H. Terashima and M. Koshi, Numerical Analysis on Unsteady Cavitation by Direct Interface Tracking Approach, Trans. JSASS Aerospace Tech. Japan, Vol. 11 (2013) (accepted)
(15)	Y. Miyashita, T. Himeno, C. Inoue, T. Watanabe and S. Uzawa, Numerical Study on Atomization Characteristics of Impinging Jets, Proceedings of 51st Conference on Aerospace Propulsion and Power, JSASS-2011-0058 (2011) (in Japanese)
(16)	C. Inoue, T. Watanabe, T. Himeno and S. Uzawa, Eulerian-Lagrangian Analysis on Liquid Sheet Atomization, Proceedings of 41stAnnual Conference of GTSJ, No.A-18 (2013) (in Japanese)