フォトブリーチング分子タグ法による乱れエネルギ収支の評価
 細川 茂雄*1 神戸大学 大学院 工学研究科  冨山 明男*1 神戸大学 大学院 工学研究科 |
Evaluation of Turbulence Kinetic Energy Budget in Turbulent Flows
気液二相気泡流は,化学プラントや熱交換器など多くの工業装置内でみられ,これらの装置の設計・開発に資する精度良い気泡流数値予測技術の構築が望まれている.気泡流は変動を伴うため,気泡流の数値予測の多くは液相の乱れに対する乱流モデルを導入しており,その多くは乱れエネルギ輸送方程式に基づいている(1)-(4).したがって,数値予測精度向上のためには気泡流における乱れエネルギ収支を把握するとともに乱流モデルの妥当性を検証する必要がある.乱れエネルギ収支の実験的評価には,瞬時局所流速と速度勾配の計測が必要である.しかし,既存の計測法ではコルモゴロフスケールより小さい空間スケールで速度勾配を測定することが難しく,乱れエネルギ消散率の評価が難しい.そこで,著者らは瞬時・局所流速および速度勾配の計測が可能な手法としてフォトブリーチング分子タグ法(PB-MTV)を開発し(5),(6),乱れエネルギの生成率,拡散率,消散率を評価できることを確認するとともに気泡流における乱流特性の理解に利用してきた(7)-(9).ここでは,PB-MTVの概要とその適用事例を紹介する.
|
2. フォトブリーチング分子タグ法
PB-MTVはフォトブリーチング反応を利用して流れ場中に印(タグ)を形成し,タグの並進運動から速度を,変形から速度勾配を測定する方法である.フォトブリーチング反応は蛍光色素がその蛍光能を失う光化学反応であり,蛍光顕微鏡による観察などでは一般的に忌避される現象である.このため,フォトクロミック反応(10)やフォトアクティベーション法(Caged dye)(11)に用いる色素に比べ,フォトブリーチング反応を起こしやすい蛍光色素は安価なものが多く,水中でのタグ形成法としてはコスト面,水溶性,熱的安定性に優れている.なお,気体を含む流体に対する種々のタグ形成法についてはKoochesfahani(12),Tropeaら(13)などを参照されたい.
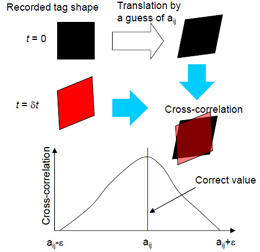
図1にPB-MTV計測装置の概略を示す.フォトブリーチング反応を呈する蛍光色素(Uranine)を混入した液体中の1点に強いレーザビーム(波長λ ~ 490 nm)を短時間(1ms程度)照射してフォトブリーチング反応を誘起した後,光束密度の低いレーザシート(λ = 450 ~ 520 nm)により反応領域を含む平面を照射すると,蛍光を発する平面内に反応領域が黒い領域(図1中の写真参照:40 ~ 100 µm)として可視化できる.レーザシートにより可視化されたタグをCCDカメラで2時刻において撮影し,タグ重心の並進運動から速度を算出する.速度勾配は図2に示す手順で評価する.まず1時刻目のタグ形状を速度勾配テンソルaijの推定値を用いて変形し,2時刻目のタグ形状との相関を算出する.その後,aijの値を変化させて各aijにおける相関値を算出し,相関値が最大となるaijを流れ場の速度勾配とする.図中では簡単のため速度勾配1成分に対して相関分布を描いているが,実際には速度勾配4成分に対する相関値分布から最大値を検索し,速度勾配を決定している.PB-MTVの詳細については,既報(5),(6)を参照されたい.なお,フォトブリーチング反応は流れ場中の任意の位置・時刻にタグを形成でき,流れの可視化にも利用できる(5).図3は水中にマトリックス状にタグを形成させた後,シリコンオイル液滴が上昇した際のタグの可視化例である.
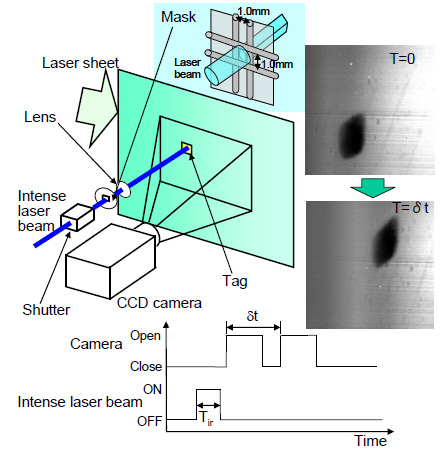
Fig. 1 Schematic of measurement system
 |
|
| Fig. 2 Schematic of cross-correlation of tag shapes | Fig. 3 Flow visualization about a drop |
3. 適用事例
3・1 単相流の乱れエネルギ収支
一辺W = 50 mmの正方形断面を有する鉛直ダクト内乱流(レイノルズ数Re = 5,000)のダクト中心断面上の壁面からダクト中心において,PB-MTVにより測定した乱れエネルギ収支とHoriuti(14)による平行平板間乱流におけるDNSの計算結果を図4に示す.乱れエネルギkの生成率P,拡散率D,消散率εは以下に示す各式にPB-MTVで測定した速度および速度勾配を代入して評価した.
| (1) | |
| (2) | |
| (3) |
ここで,Uは平均速度,u’は変動速度,νは動粘性係数を表す.ただし,拡散率中に現れる圧力拡散項は無視した.また,図4の乱れエネルギ収支はuτ4/ν(uτ:摩擦速度)で無次元化している.PB-MTVの計測結果はDNSによる計算結果と良好に一致している.ただし,PB-MTVで測定したε+の絶対値は全域でDNSよりわずかに大きくなっている.これは,εが速度勾配の2乗平均項であるため,個々の速度勾配のランダム誤差が平均値に正のバイアス誤差を生むためである.PB-MTVにおけるP+, D+, ε+の残差(P++D+-ε+)は小さく,P+の最大値のおよそ15%以内であり,乱れエネルギ評価の最大誤差も15%程度と見積もれる.なお, PB-MTVではダクト内乱流を,DNSでは平行平板間乱流を対象としていることから生じる差もこの値には含まれている.また,Horiuti(14)のDNS結果から実験において無視した圧力拡散はP+の最大値の5%以内であり,乱れエネルギ収支評価において圧力拡散項を無視した影響は小さい.このことは,D+の測定値が圧力拡散を含むDNSのD+と良好に一致していることからも確認できる.以上より,PB-MTVは圧力拡散が小さい乱流における乱れエネルギ収支を良好に測定できると結論できる.なお,PB-MTVの速度・速度勾配測定精度は画像上の0.1 pixel程度に対応することを確認しており(6),タグの画像解像度を向上することにより速度・速度勾配測定精度が向上し,乱れエネルギ収支評価精度もさらに向上すると考えられる.
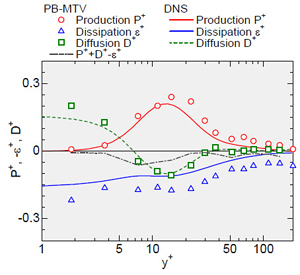
Fig. 4 Turbulence kinetic energy budget
3・2 気泡流の乱れエネルギ収支
PB-MTVを前述と同じ鉛直ダクト内乱流(液相体積流束JL = 0.06 m/s, Re = 5,000)に気泡を混入した気泡流(気相体積流束JG = 5.0 x 10-5 m/s, 気泡径d =0.3 ~ 1.5 mm)に適用し,気泡が乱れエネルギ収支に及ぼす影響を調べた.図5に気泡流と単相流における乱れエネルギ収支を示す.ε+は単相流と気泡流で大きく変化しないが,P+およびD+は気泡の存在により変調している.その結果,単相流においてP+, D+, ε+の残差(P++D+-ε+)はほぼ零であるのに対し,気泡流では残差が零にならない.流れが定常で準発達状態であることから,これらの結果は本実験で対象とした気泡流では乱れエネルギ生成率および拡散率が式(1)および(2)のみで表わさせないこと,即ち乱れエネルギ輸送方程式に基づく気泡流の数値予測においてはP,Dのモデル化が必要であることを示唆している.一方,気泡の有無によるε+の変化が小さいことから,少なくとも本実験範囲では小さいスケールで生じる乱れエネルギの消散に及ぼす気泡の影響は小さいと考えられる.
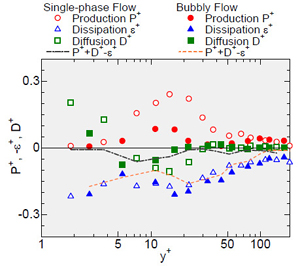
Fig. 5 TKE budgets in single-phase and bubbly flows
KataokaとSerizawa(15)は気液二相乱流における基礎方程式を導出し,気液間の運動量輸送により乱れエネルギが生成することを示した.TroshkoとHassan(3)はこの気泡が誘起する乱れの生成率PBを次式で評価し,k-εモデルを用いた数値計算を行っている.
| (4) |
ここで, URは気液間相対速度,Cdは気泡の抗力係数である.気泡流におけるP+とPB+の和をD+およびε+とともに図6に示す.前述の通り気泡流ではP+, D+, ε+の残差(P++D+-ε+)は零にならないが,PB+を加えることにより残差(P++PB++D+-ε+)は零に近づく.本結果は(1) 気泡流における乱れエネルギ生成率はTroshkoとHassan(3)が提案する式(4)と式(1)の線形和により概ね評価できること,(2) 気泡による乱れエネルギ生成率の増加は気液間の運動量輸送に起因すること,および(3) せん断流および気泡により生成された乱れエネルギはカスケード過程を経て単相流と同様に消散することを示唆している.なお,このような結果は局所平衡を仮定した乱れエネルギ収支分析では得られず,PB-MTVによる乱れエネルギ収支評価の有用性が再確認できる.
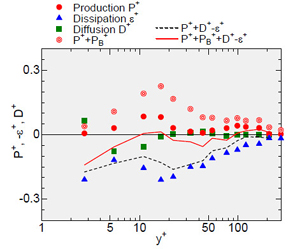
Fig. 6 TKE budget in bubbly flow
3・3 k-εモデルの検証
気泡流における生成率がPB(式(4))とP(式(1))の線形和により概ね評価できることを示したが,数値計算に当たってはせん断誘起乱れのP,D,εのモデルが必要となる.多くの場合,単相流用のk-εモデル等が用いられているが,気泡流におけるその妥当性はほとんど検証されていない.k-εモデルではPを次式でモデル化している.
| (5) |
ここで, ![]() は平均ひずみ速度テンソル,νTは渦動粘性係数であり,低レイノルズ数型k-εモデルでは次式で与えられる.
は平均ひずみ速度テンソル,νTは渦動粘性係数であり,低レイノルズ数型k-εモデルでは次式で与えられる.
| (6) |
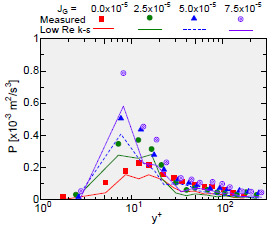
ここで,Cµは係数(= 0.09),fµは減衰関数であり,ここでは安倍ら(16)の式を用いた.PB-MTVでは,局所の速度,速度勾配,k,εが測定できるため,モデル式(式(5), (6))の右辺に測定値を代入することにより,モデル自体の成立性が調べられる.図7は前述の鉛直ダクト内気泡乱流においてJG を0.0 ~ 7.5 x 10-5 m/sの範囲で変化させたときのPの測定値およびモデル式に測定値を代入して求めた値を示している.なお,気泡径は3・2節の実験より少し小さくd = 0.2 ~ 1.0 mmである.PはJGの増加とともにy+ = 8付近で急激に増加するが,y+ > 20ではJGの影響が小さい.モデル式の値はこのような傾向を良く再現しており,単相流(JG = 0.0 m/s)での両者の値の差を踏まえれば,上記モデル式は気泡流においてもおおむね良好にせん断誘起乱れの生成率を評価できると言える.
同様にPB-MTVによる測定結果を用いて,他の項やεの方程式などに関してもモデルの妥当性を直接検討できる.図8は,PB-MTVで測定した速度・速度勾配から算出したεの生成率Pεと低レイノルズ数型k-εモデルにおけるPεのモデル式の比較である.データのばらつきはあるもののJGの増加とともにPεは増加傾向にあり,モデル式もおおむねこの傾向を捕らえていることがわかる.精緻な議論,一般的な結論を得るためには,さらに実験を重ねる必要があるが,以上の結果からPB-MTVを用いることによる乱流モデルの実験的検証の可能性が確認できる.なお,実験の詳細および他の項に関する議論については既報(9)を参照されたい.
 |
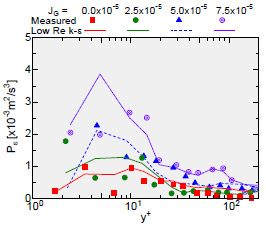 |
| Fig. 7 Production rate of k | Fig. 8 Production rate of ε |
4. おわりに
フォトブリーチング分子タグ法(PB-MTV)の概要とその適用事例の紹介を通して,(1) PB-MTVが乱れエネルギ収支評価手法として有用であること,(2) 気泡流では気液間の運動量輸送により乱れエネルギ生成率が増加し,せん断誘起乱れの生成率と拡散率,消散率のみの和は零にならないこと,および (3) PB-MTVにより乱流モデルの実験的検証の可能性が開けることを示した.
分子タグ法は任意の時刻に流れ場中の任意の位置に印を付けることが可能であり,散乱粒子のような追従性,ブラウン運動などに起因する問題も生じないため,今後さらに幅広い応用範囲が期待できる.本稿が読者の研究の参考になれば幸いである.
謝 辞
本研究の一部は科学研究費補助金 基盤研究(C)(課題番号22560167)の助成を受けて実施した.
文 献

