直交格子を用いた熱流体シミュレーションの高精度化

佐藤 範和*1

竹内 伸太郎*2 梶島 岳夫*2 稲垣 昌英*1 堀之内 成明*1 *1 (株)豊田中央研究所 *2 大阪大学

Accuracy improvement of the Cartesian grid method for numerical simulations of heat transfer and fluid flow

Norikazu SATO^*1, Shintaro TAKEUCHI^*2, Takeo KAJISHIMA^*2, Masahide INAGAKI^*3 and Nariaki HORINOUCHI^*3

^*1 Toyota Central R&D Labs., Inc., 41-1 Yokomichi, Nagakute, 480-1192 Japan, nsato[at]mosk.tytlabs.co.jp
^*2 Osaka University
^*3 Toyota Central R&D Labs., Inc.

1. はじめに

　産業界では，製品の性能予測や現象解明を目的として CFD（Computational Fluid Dynamics）が積極的に用いられている．また，環境やエネルギー問題への対応をはじめ，新規技術の創出に向けた研究開発においてもCFDは重要な役割を担っている．これらのシミュレーションでは，実機の複雑な形状を詳細に再現することが重要である．しかし，一般に用いられる境界適合型の計算格子（図1(a)，(b)）では，格子生成に多大な時間と労力が必要になる場合が多く，格子生成の簡略化とそれによるターンアラウンドタイムのさらなる短縮は，CFDを実用的に利用するうえでの技術課題の一つである．

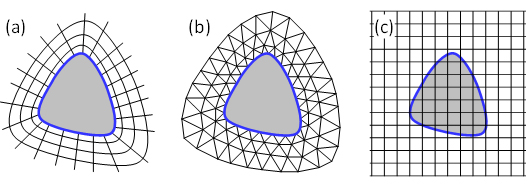図1 計算格子の種類：(a) 構造格子，(b) 非構造格子，(c) 直交格子

　 本課題を解決するための有力な計算方法として直交格子法が挙げられる．直交格子法は，図1(c)に示すように，直交の計算格子上で任意の物体形状を表現する計算方法であり，物体形状を階段状に近似したボクセル法⁽¹⁾や，より高次の計算法であるImmersed Boundary法^(2)(3)(4)(5)など様々な方法が提案されている．しかし，物体境界と計算格子の不一致に起因した形状再現性の低下と計算精度の低下が課題であり，実用問題への展開の阻害要因となっている．そこで，著者らは直交格子法の高精度化のための離散化手法を新たに提案した⁽⁶⁾⁽⁷⁾．ここでは，その概要と精度検証事例について述べるとともに，最近の取り組みを紹介する．

　なお，直交格子法は，今回注目する複雑形状流れ問題への利用以外にも，固体変形をともなう移動境界流れや混相流など様々な適用先が想定されており，現時点では計算精度や計算負荷など，それぞれの解析対象への適性に応じて使い分ける必要がある．直交格子法の系統的な解説については文献⁽⁸⁾⁽⁹⁾などを参照されたい．

 

2. 速度場に対する直交格子法の概要

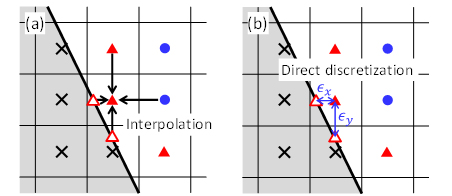図2 直交格子法の比較と計算セルの分類：(a) IB法（Direct Forcing型），(b) 提案法 ，●流体セル，×物体セル，▲境界セル

(a) 計算対象


(b) 流速分布
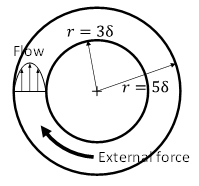
図3 同軸二重円筒間流れでの精度検証

　本研究で提案する直交格子法の離散化については，著者らの論文⁽⁶⁾⁽⁷⁾に詳しく述べているので，ここでは離散化の概略のみを説明する．

　 図2のように，計算セル中心が流体側に属する計算セルを“流体セル”，物体（固体）側に属する計算セルを“物体セル”とし，流体・固体界面に隣接する流体側の計算セルを“境界セル”と定義する．複雑形状をともなう非圧縮性流体計算で広く用いられるDirect Forcing型のImmersed Boundary（IB）法⁽⁴⁾では，境界セルの流速を周囲の流体セルでの流速と壁面上の速度（静止壁の場合はすべりなし条件）からの補間で与える（図2(a)）．これによる高い計算安定性と組み込みの容易さから幅広い対象で利用されているが，一方で，境界セルではNavier-Stokes方程式を解かないため，実用問題で想定される格子解像度の低い条件では，計算精度の大幅な低下が懸念される．また，一部の方法では，速度の補間操作と圧力方程式の離散化とが整合しておらず，速度の境界条件が満足されないことも指摘されている^(10)(11)．

　 これら二つの問題に対し，次の考えに基づく離散化手法を新たに提案した⁽⁶⁾．まず，境界近傍での補間操作に起因した精度低下を抑制するため，境界セルにおいてもセル中心と境界間の距離を用いることでNavier-Stokes方程式を直接的に離散化する（図2(b)）．その離散化式に準じ，圧力方程式に対してもセル中心と境界間の距離を利用した離散化を行うことにより，速度場と圧力場の離散化の整合性を満足させる．一般に，IB法では物体の存在を強制外力で表現するが，以上の境界セル特有の速度場と圧力場の離散化は，IB法における強制外力に相当するとみなすことができる．

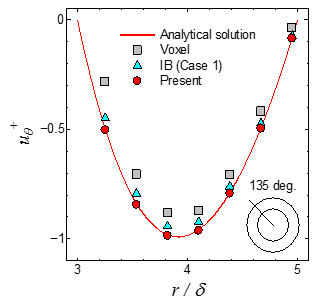
　 まず，図3(a)に示す同軸二重円筒間流れにおける精度検証の結果を示す．本問題は，解析解が存在し，なおかつ格子と境界間の位置関係の規則性が少ないことから精度検証に適している．摩擦速度と流路半幅に基づくレイノルズ数は2である．図3(b)の流路断面内の速度分布より，提案法の速度分布は，境界を階段近似したボクセル法やDirect Forcing型のIB法⁽⁴⁾（IB Case 1）に比べて解析解に良好に一致しており，壁面摩擦応力の予測誤差についても他の手法に比べて大きく低減されることを確認している（図省略） ．

　次に，円柱の周りの流れについて，非定常渦放出をともなうレイノルズ数200の場合の検証結果を示す．ここでは，境界適合（Boundary-Fitted Curvilinear Coordinate，BFC）格子の計算を別途実施し，基準解として用いた．図4(a)の円柱表面上の圧力分布より，提案法では，低格子解像度（格子間隔／円柱直径=0.05）時にθ=90°付近で解像度不足に起因した圧力振動が確認されるが，その影響は限定的であり，円柱の背圧は基準解と良好に一致している．図4(b)には，抵抗係数の時間刻み（クーラン数）に対する依存性を調べた結果を示す．速度場と圧力場の離散化の整合性を考慮したIB法⁽¹¹⁾（IB Case 2）や提案法では，これを考慮していないIB法⁽⁴⁾（IB Case 1）に比べて，時間刻みに依存せずに抵抗係数が精度良く求まる．さらに，提案法では，境界セルにおいても基礎式を直接的に離散化したことにより計算精度が向上し，基準解であるBFC格子に最も近い結果が得られる．

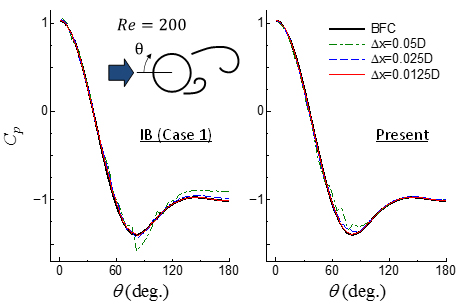
(a) 円柱表面上の圧力分布


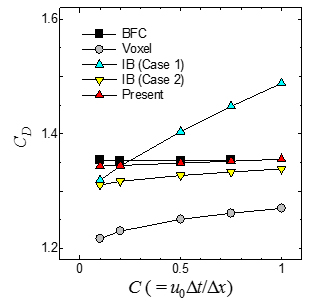
(b) 抵抗係数のクーラン数依存性
図4 円柱周りの流れでの精度検証

 

3. 温度場への拡張

　 提案法における境界セルでの離散化の考え方は，伝熱計算との親和性も高く，温度場への拡張も行っている．温度場を考慮した流体シミュレーションでは，規定された温度境界条件のもとで熱対流場のみを扱う場合に加え，流体・固体間の熱の授受を考慮し，固体内部の熱伝導との連成問題まで扱う場合もある．以下では，それぞれの問題への提案法の展開について紹介する．

3.1 対流熱伝達問題のための直交格子法⁽⁷⁾

　 温度場の基礎方程式であるエネルギー方程式に対し，速度場と同様に，境界セルでも物体の位置とそこでの温度境界条件（ディリクレ（等温）条件，ノイマン（等熱流束・断熱）条件）に基づき直接的に離散化する．直交格子上でノイマン条件を適切に扱うために必要となる，境界上の接線方向の温度勾配は，周囲の温度場からの外挿により与える．図5(a)の同軸二重円筒間流れを対象に温度場の精度検証を実施した．温度境界条件として，内壁には周方向角度に依存した温度分布をディリクレ条件で与え，外壁には断熱条件を課した．図5(a)に，基準計算であるBFC格子の温度分布と提案法の温度分布，図5(b)には外壁温の周方向分布を示す．ボクセル法や，Direct Forcing型のIB法に準じた方法（IB Case A）では，外壁上の温度分布に基準解（BFC格子の結果）との明確な差が認められるのに対し，提案法では良好な一致が得られており，ノイマン条件を課した境界上で接線方向に強い温度勾配が存在する場合にも精度が維持されることがわかる．

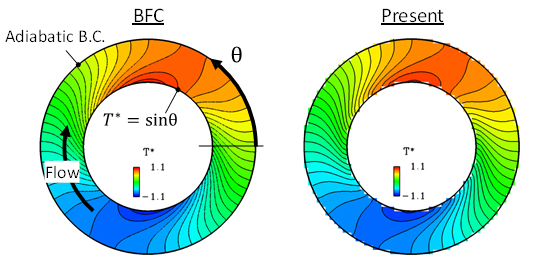
(a) 温度分布の比較


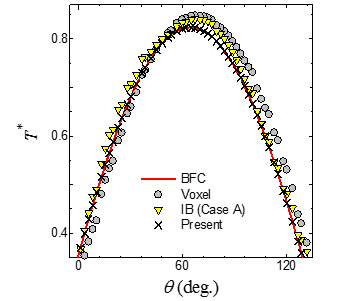
(b) 外壁上の温度分布
図5 同軸二重円筒間流れでの温度場の精度検証

3.2 流体・固体間の熱連成問題のための直交格子法⁽¹²⁾

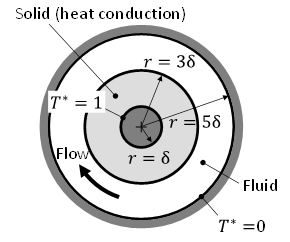
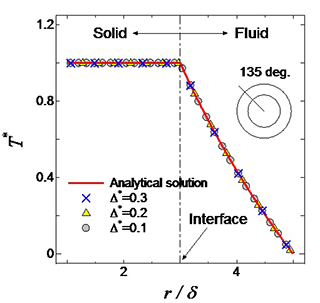
　 流体・固体間の熱の連成問題を扱う場合についても，流体・固体の各相においてエネルギー方程式を直接的に離散化する．境界セル上の熱流束については，接線方向成分と法線方向成分とに分解し，それぞれを流体・固体界面で成り立つべき温度の関係式に基づいて求める．固体熱伝導をともなう同軸二重円筒間流れ（図6(a)）で精度検証を行った結果を図6(b)に示す．提案法では，空気と銅のような高物性比の条件においても，安定かつ精度良く温度分布を予測できており，界面上の熱流束が適切に評価されていることがわかる．

(a) 計算対象


(b) 半径方向の温度分布
図6 固体熱伝導をともなう同軸二重円筒間流れでの温度場の精度検証
（銅－空気相当：λ_s/λ_f=15000，(ρc)_s/(ρc)_f=2850）

 

4. おわりに

　 熱流体シミュレーションの利便性の向上を目指した直交格子法について，その課題である精度向上のための離散化手法，ならびに熱対流や熱伝導をともなう温度場計算への展開について紹介した．提案法は伝熱問題以外にも薄板や移動境界問題への適用も検討されており⁽¹³⁾，その適用範囲は拡大しつつある．また，例えば図7に示すような，従来の格子系では計算が困難である複雑形状の熱流動場を良好な精度で再現できることも確認しており，提案法は，設計・開発現場での多様な解析ニーズに応えるシミュレーション技術として有用であると考える．

(a) 金網近傍の拡大図

(b) 流れ場
図7 応用事例（金網を通過する流れ）

 

文　献

(1)	Ono, K., Tomita, N., Fujitani, K. and Himeno, R., “An application of voxel modeling approach to prediction of engine cooling flow”, JSAE Spring Convention Proceedings, No. 984 (1998), pp. 165-168.
(2)	Peskin, C.S., “Flow patterns around heart valves: a numerical method”, Journal of Computational Physics, Vol. 10 (1972), pp. 252-271.
(3)	Mohd-Yusof, J., “Combined immersed-boundary/B-spline methods for simulations of flow in complex geometries”, Center for Turbulence Research Annual Briefs, (1997), pp. 317-327, Stanford University.
(4)	Fadlun, E.A., Verzicco, R., Orlandi, P. and Mohd-Yusof, J., “Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations”, Journal of Computational Physics, Vol. 161 (2000), pp. 35-60.
(5)	Kajishima, T. and Takiguchi, S., “Interaction between particle clusters and particle-induced turbulence”, International Journal of Heat and Fluid Flow, Vol. 23 (2002), pp. 639-646.
(6)	佐藤範和, 梶島岳夫, 竹内伸太郎, 稲垣昌英, 堀之内成明, “直交格子法における物体境界近傍の直接離散化法（速度場と圧力場の整合性を考慮した高精度化）”, 日本機械学会論文集B編, Vol. 79, No. 800 (2013), pp. 605-621.
(7)	佐藤範和, 竹内伸太郎, 梶島岳夫, 稲垣昌英, 堀之内成明, “直交格子を用いた対流熱伝達計算における物体境界近傍の直接離散化法”, 日本機械学会論文集B編, Vol. 79, No. 803 (2013), pp. 1219-1231.
(8)	梶島岳夫, 竹内伸太郎, “固気液混相流の直接数値シミュレーション”, 日本機械学会論文集B編, Vol. 76, No. 765 (2010), pp.712-719.
(9)	Mittal, R. and Iaccarino, G., “Immersed boundary methods”, Annual Review of Fluid Mechanics, Vol. 37 (2005), pp. 239-261.
(10)	Kim, J., Kim, D. and Choi, H., “An immersed-boundary finite-volume method for simulations of flow in complex geometries”, Journal of Computational Physics, Vol. 171 (2001), pp. 132-150.
(11)	Ikeno, T. and Kajishima, T., “Finite-difference immersed boundary method consistent with wall conditions for incompressible turbulent flow simulations”, Journal of Computational Physics, Vol. 226 (2007), pp. 1485-1508.
(12)	佐藤範和, 竹内伸太郎, 梶島岳夫, 稲垣昌英, 堀之内成明, “固体熱伝導をともなう対流伝熱問題のための直交格子法”, 第28回数値流体力学シンポジウム, E09-1 (2014).
(13)	Fukuoka, H., Takeuchi, S. and Kajishima, T., “Interaction between fluid and flexible membrane structures by a new fixed-grid direct forcing method”, 11th International Conference of Computational Methods in Sciences and Engineering, (2015).