半開放形プロペラファンにおける翼端渦の三次元構造に関する研究
 草野和也 九州大学大学院 (現 (株)日立製作所) |
 古川雅人 九州大学大学院 |
 山田和豊 九州大学大学院 |
Kazuya KUSANO*1, Masato FURUKAWA*2 and Kazutoyo YAMADA*2 |
||
1. はじめに
プロペラファンは空調機や電子機器などに組み込まれ,送風および冷却の用途に広く使用されている.このようなプロペラファンでは,設置スペースの制約から,図1に示すように,動翼のまわりには軸方向長さの短いシュラウドのみが装着され,翼前縁および翼先端の一部が上流に開放される半開放形の形態となる場合が多い.半開放形プロペラファンの流れ場は,翼全体がケーシングで完全に覆われた軸流ファンとは異なり,外部流れと内部流れが混在し,強い三次元性を呈する.過去の研究により,動翼先端から強い縦渦として巻き上がる翼端渦が半開放形プロペラファンの空力性能および騒音に重要な影響を及ぼすことが知られている(1),(2).これまでに,実験による研究が多数行われてきたが(3)-(8),動翼まわりの三次元流れ場を計測によって把握するのは困難であり,翼端渦の性質については十分な理解が得られてはいなかった.
そこで著者らは,エアコン室外機用の半開放形プロペラファンを対象として,DES(Detached Eddy Simulation) による大規模な数値解析を行い,得られた流れ場から後処理として渦構造を的確に抽出することによって,翼端渦の挙動を明らかにした(9).ここでは,解析手法と得られた知見について紹介する.
Fig. 1 Time-averaged vortex structures and limiting streamlines on blade surfaces |
2. 数値解析手法
2・1 Detached Eddy Simulation
流れ解析として,k - ω 二方程式モデルに基づくDES(Detached Eddy Simulation)(10)を実施した.周方向に周期境界条件を適用することにより,動翼間1ピッチのみを計算した.計算格子の総セル数は4600万程度である.翼面に垂直方向の最小格子幅はy+<1を満足し,また,翼コード中央付近における翼端渦の渦核領域内にはその直径方向に20セル程度の計算セルを配置した.以下では,解析結果として時間平均化された流れ場について示す.
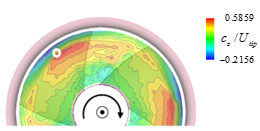
図2に動翼下流における軸方向速度分布について,DES解析結果とLDV計測結果の比較を示す.白丸で示す翼端渦中心の位置およびその周りの速度分布について両者は定量的に良い一致を示しており,DES解析の妥当性が確認できる.
|
|
(a) LDV |
(b) DES |
Fig. 2 Time-averaged axial velocity distributions downstream of rotor (ϕ=0.291) |
|
2・2 三次元渦の同定法
ターボ機械における渦中心の同定法については,著者らの一人が詳細に解説している(11).本研究では,その中の特異点理論に基づくSawadaの方法(12)を用いた.また,渦構造を画像で表示する際には,Furukawaらの渦中心の存在率の定量化(13)に従い,その等値面により表示した.図1に半開放形プロペラファンまわりの渦構造の可視化例を示す.渦構造は無次元ヘリシティで色付けされており,その絶対値によってせん断層と縦渦を識別することができる.さらに,その符号によって流れ方向に対する渦の回転方向を確認できる.動翼先端付近において,翼端渦が大規模な縦渦構造として鮮明に描画されている.その他に,負圧面の前縁はく離渦や翼根付近のコーナーはく離渦などの比較的小規模な渦構造も観察される.
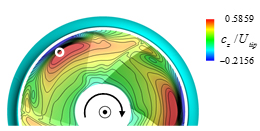
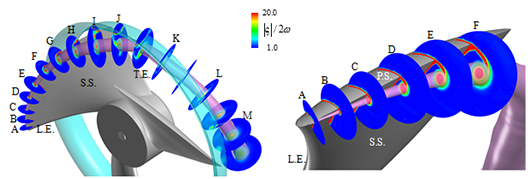
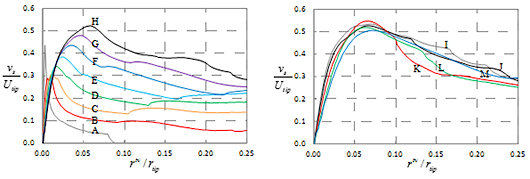
さらに本研究では,翼端渦についてその流れ方向挙動を詳細に調べた.その際,三次元曲線として同定された翼端渦中心の局所位置において,その渦軸方向に対して垂直な断面上に計算格子上の物理量をマッピングした.図3に翼端渦に垂直な断面における可視化例として,渦度の絶対値分布を示している.また,このようにして抽出した渦中心まわりの流れ場から渦核領域を同定した.具体的には,図4に示す渦軸まわりの周方向に平均化した旋回速度の半径方向分布において,その旋回速度が最大を示す半径位置より内側の領域を渦核領域とした.同定された翼端渦の渦核領域の外縁を図3中の桃色の半透明面で示している.渦核を同定することによって,循環を定量的に評価することが可能となる.
|
|
(a) Overall view |
(b) Around blade tip |
Fig. 3 Trajectory of tip vortex core and absolute vorticity distributions on cross-sections perpendicular to tip vortex |
|
|
|
(a) A-H (Opened region) |
(b) I-M (Ducted region) |
Fig. 4 Distributions of tangential velocity around tip vortex |
|
3. 翼端渦の三次元構造
3・1 翼端渦中心の軌跡
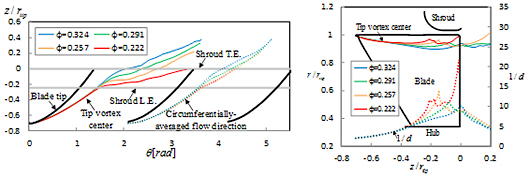
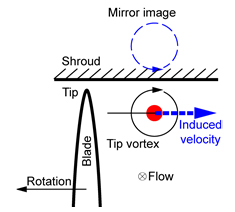
図5に同定した翼端渦中心の軌跡を翼端面および子午面に投影して示している.同図において,ϕは流量係数であり,4つの流量条件について示している.シュラウドに覆われていない開放領域では,翼端渦は点線で示す主流に沿って移流しており,その軌跡は流量により変化しない.一方,シュラウド面下では,翼端渦は周方向(隣接翼の方向)に転向している.これは,図6に模式的に示すように,翼端渦がシュラウド壁面近傍に位置している場合,その鏡像により翼端渦に周方向の速度が誘起されるためである.プロペラファンの動翼下流においては,シュラウドが存在しない上に,流れは旋回速度成分をもち,その旋回成分は流量の低下とともに増加することから,低流量作動点では大きな旋回成分に伴う遠心力の作用により動翼下流の流れは半径外向きに大きく傾く.その結果,図5(b)に示すように,流量の低下とともに翼端渦がシュラウド面に近づき,シュラウド面下における翼端渦の周方向への転向がより大きくなる.したがって,シュラウドの形状や取付け位置などにより動翼下流の半径外向き流れを抑制することで,ファン性能を向上できる可能性がある.
|
|
(a) θ-z plane |
(b) r-z plane |
Fig. 5 Trajectory of tip vortex center |
|
|
Fig. 6 Illustration of interaction mechanism between tip vortex and shroud wall |
3・2 翼端渦の流れ方向挙動
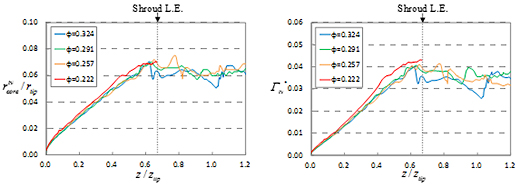
図7および図8に渦核半径および循環について流れ方向の変化をそれぞれ示す.開放領域では,翼端渦の渦核半径と循環は流れ方向に線形的に増加し,シュラウド前縁付近で最大となっている.これは,図3に見られるように,開放領域では動翼先端から渦度が供給されるためである.一方,シュラウド面下では,翼端渦の循環と渦核半径は減少傾向にあり,翼端渦は緩やかに減衰する.循環と渦核半径の流れ方向挙動に関して流量による大きな差異は見られない.また,翼端渦の最大循環量は動翼先端付近から流出する循環量の60~75%程度である.さらに,その渦核半径の最大値は翼先端半径の7%程度である.
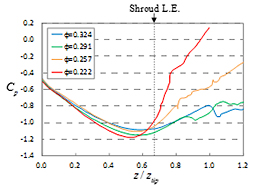
次に,翼端渦中心に沿った静圧係数の分布を図9に示す.開放領域では,翼端渦の成長に伴って翼端渦まわりの循環が流れ方向に増加する結果,翼端渦中心の静圧は流れ方向に低下する.一方,シュラウド面下では,翼端渦の減衰が始まることおよび動翼の仕事による主流の圧力上昇が顕著になることから,翼端渦中心の静圧は流れ方向に上昇する.
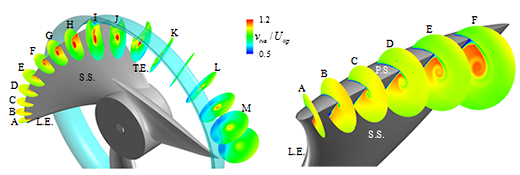
図10は翼端渦に垂直な断面における渦軸方向の速度成分の分布である.翼端渦の巻き上がり直後の断面BおよびCでは,渦中心付近の渦軸方向速度が周囲よりも小さいウェークタイプの速度分布が見られる.一方,それより下流側では,図9に示した翼端渦の急速な成長に伴う流れ方向の大きな順圧力勾配に起因して,渦中心に最大速度をもつジェットタイプの渦軸方向速度分布が形成される.したがって,翼端渦が軸方向を向いていれば,翼端渦によるブロッケージ効果が小さくなり,翼先端部での流量低下を抑制することができると考えられる.
|
|
Fig. 7 Tip vortex core radius |
Fig. 8 Tip vortex circulation |
|
Fig. 9 Distributions of static pressure coefficient along tip vortex |
|
|
(a) Overall view |
(b) Around blade tip |
Fig. 10 Distributions of velocity component along tip vortex axis direction on cross-sections perpendicular to tip vortex |
|
4. おわりに
DESおよび渦同定法を用いて,半開放形プロペラファンにおける複雑な三次元渦流れを解析した事例を紹介した.得られた知見がファン設計の一助となれば幸いである.また,紹介した渦同定法が流体機械の流動解析において広く活用されることを期待したい.
文 献