乱流境界層の平均量特性に対する粗さの影響

亀田 孝嗣 近畿大学工学部	望月 信介 山口大学工学部	大坂 英雄 山口大学名誉教授

1．はじめに

　乱流境界層に関する壁面粗さの影響は長らく携わってきた研究課題です．我々は粗さ形状が単純でかつはく離点が固定される二次元矩形粗さに限定して，粗さ要素の配置間隔(粗さピッチ比)による粗面上の流れ特性の違いを生じさせる根源は何かを出発点として研究を進めてきました．一連の研究から，流れ特性の違いは境界層厚さに対して数％程度の大きさである粗さ要素近傍周辺の流れを詳細に調査することで議論可能であると考え，実験を進めてきました．

　 以下に表記タイトル受賞論文(2017年度日本機械学会賞（論文）)の内容の一部である粗さ要素近傍流れの計測結果と解析解による表現，および対数速度分布の粗さ関数と粗さピッチ比の関係に限定して述べます．

2．実験対象の流れ場と計測装置

 
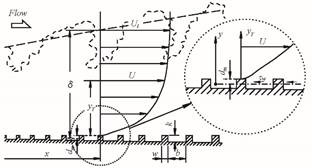
Fig. 1 Flow field, nomenclature and symbols.

　図1に実験対象とした流れ場を示します．使用した平板は，二次元矩形粗さ要素の粗さ高さが流れ方向距離に対して比例(1.25×10^-3)する粗面です．この粗面上に発達する乱流境界層の特徴は，Rotta(1962)やTalluruら(2016)によると，境界層内の平均量分布に対するレイノルズ数依存性が無視されます．粗さ要素の配置間隔は粗さピッチ比(=，は溝部幅およびは粗さ要素幅です．)=4 です．この値において，壁面抵抗に対して圧力抵抗が支配的になります(亀田他, 2007，Leonardi et al., 2003)．座標系は，平板前縁に原点を置いた流れ方向距離を，粗さ要素上面からの垂直方向距離をおよびスパン方向距離をとした直交座標系です．また，は粗さ要素後端からの流れ方向距離，(=，は排除高さで壁面抵抗のモーメント中心から粗さ要素上面高さまでの距離)は壁面抵抗のモーメント中心からの垂直方向距離です．

　 計測は=2180付近の粗さ要素一ピッチの範囲で行われ，この位置における運動量厚さに基づくレイノルズ数(=，は主流速度，は運動量厚さおよびは動粘度です．) および粗さレイノルズ数 (= ，は摩擦速度) はそれぞれ6000および149です．

　 粗さ底層内の速度計測には 2-Channel  LDV システム(TSI IMF-750，4WAr-Ion，焦点距離 350 mm)を使用しています．粗さ要素壁面近傍において壁面とレーザー光の干渉を避けるために一次元計測を採用して，速度の一次および二次モーメントを求めています．

3．結果と考察

3・1　粗さ底層内の平均速度分布
　粗さ底層内溝内部領域おいて溝部幅当たりに平均化された流れ方向のレイノルズ方程式は，

(1)

と表せます．式(1)中のは，時間平均値の溝部幅平均値を意味し，

(2)

と定義します．およびは，流れ方向および垂直方向時間平均速度およびの溝部幅平均速度およびからの偏差です．は平均流線の波打ちによる見かけのせん断応力=，レイノルズせん断応力=および粘性せん断応力=の和であり，本粗面の実験条件ではとなります．式(1)の各項を混合距離でモデル化し，分布の相似性を期待すると，式(1)の解として，

(3)

が得られます．式(3)中のは溝上部領域に形成されるはく離せん断層の流れの駆動力である方向単位幅当たりの圧力抵抗に基づき定義された速度

(4)

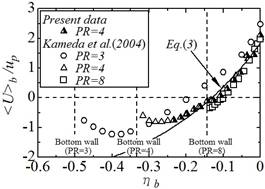
Fig.2 Spatially-averaged streamwise mean velocity profiles.

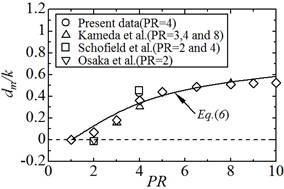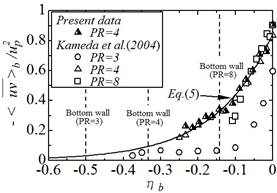
Fig.3 Spatially-averaged Reynolds shear stress profiles.	Fig.4 Displacement height.

で，は溝部幅ではく離せん断層の発達距離に関係する長さです．式(3)中の係数は10.3，6.60，0.519および-3.04です．図2に分布を示します．溝底面(図中，縦の破線)付近を除いて48の範囲において分布は式(3)によって表現されます．

　式(3)を利用すると，レイノルズせん断応力と壁面抵抗のモーメント中心から粗さ要素上面高さ位置までの距離は以下の式で表せます．

	(5)
	(6)

式(5)および(6)中のは0.301であり，48の範囲において実験結果と良好に一致します(図3および図4参照)．

3・2　対数速度分布
　ここでは，粗さ底層内の平均速度分布(式(3))と粗さ底層上部の平均速度分布の接合性から，粗さ関数への粗さピッチ比の影響を議論します．式(3)の溝部幅当たりの平均速度分布を粗さ一ピッチ当たりの平均速度分布へ書き直すと，

(7)

となります．ここで，はです．また，は

within a cavity

(8)

と定義します．粗さ底層上部の対数層の平均速度は，従来の対数速度分布式

(9)

で表します．粗さ要素高さの定数倍の高さを粗さ厚さ()とし，その高さ()で式(7)と(9)が接合すると，

	(10)
	(11)

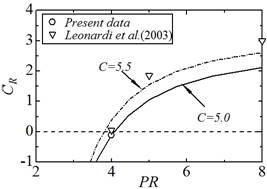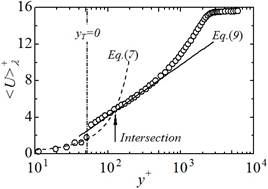
Fig. 5 Logarithmic mean velocity profile.	Fig.6 Constant of roughness function.

と表せます．接合高さは本実験結果(図5参照)から決定され，0.800です．図6に粗さ関数の定数項のに対する変化を示します．本実験結果および二次元チャネル流におけるDNSの結果(Leonardi et al., 2003)が図示されています．図中の実線と破線は式(10)および(11)を乱流境界層において従来よく使用される5.0およびLeonardiらの論文中(2003)で使用している5.5で描かれたものです．実線および破線はぞれぞれ乱流境界層の本実験結果および二次元チャネル流のDNS結果を良好に表現しています．この結果より，粗さ底層内の平均速度分布や粗さ底層厚さが粗さ関数の大きさを決定するため，粗さ底層は粗面流における重要な研究対象です．

4．おわりに

　乱流境界層に対する粗さの影響を議論するために，壁面近傍の粗さ底層内の流れに着目し，詳細な速度計測と運動方程式に基づく解析を行いました．解析結果を使用することで，平均速度に対する粗さ，ここでは粗さピッチ比，の影響が48の限られた範囲の値において議論可能です．他の値では粗さ底層の流れの代表尺度を検討し，同様な解析をすることで粗面流の特徴を説明することができると考えています．

参考文献

Kameda, T., Mochizuki, S. and Osaka,H., Investigation of the level of action on wall shear stress and the law of the wall for rough wall turbulent boundary layer, Transactions of the Japan Society of Mechanical Engineers, Series B, Vol.73, No.733(2007), pp.1821-1828(in Japanese).
Kameda, T., Osaka, H. and Mochizuki, S., Effect of roughness pitch ratio on the structures in the vicinity of a roughness element for the turbulent boundary layer developing over k-type rough walls arranged with two-dimensional square ribs, Transactions of the Japan Society of Mechanical Engineers, Series B, Vol.70, No.697(2004), pp. 2303-2310(in Japanese).
Leonardi S., Orlandi P., Smally R.J., Djenidi L. and Antonia R.A., Direct numerical simulations of turbulent channel flow with transverse square bars on one wall, Journal of Fluid Mechanics, Vol.491(2003), pp.229-238.
Osaka, H., Sakamoto, M. and Kageyama, Y., Turbulent structures in the vicinity of the roughness element for a boundary layer over a d-type rough surface, Transactions of the Japan Society of Mechanical Engineers, Series B, Vol.52, No.478(1986), pp.2360-2366(in Japanese).
Rotta, J.C., Turbulent boundary layers in incompressible flow, Progress in Aerospace Sciences. Vol.2(1962), pp.96-129, Elsevier Ltd.
Schofield, W.H., Perry, A.E. and Joubert, P. N., Similarity relations for pressure distributions on slot type rough walls under turbulent boundary layers, Transactions of ASME, Journal of Fluid Engineering, Vol.96, No.2(1974), pp.186 -188.
Talluru, K.M., Djenidi, L., Kamruzzaman, Md. and Antonia, R.A., Self-preservation in a zero pressure gradient rough-wall turbulent boundary layer, Journal of Fluid Mechanics, Vol.788(2016),pp. 57-69.