ポート噴射エンジン用多孔スワールインジェクタによる噴霧の微粒化に関する研究

吉村 一樹 株式会社日立製作所	安川 義人 株式会社日立製作所	石井 英二 株式会社日立製作所	小林 信章 日立オートモティブ システムズ株式会社

1.　はじめに

近年，自動車市場ではエンジンの排気性能向上と燃費の改善が市場課題となっており，燃料インジェクタの微粒化性能向上が求められている．本研究では微粒化性能の高い旋回（スワール）方式と，噴霧形状制御が容易な多孔方式を組み合わせた多孔スワールインジェクタにおいて，噴霧干渉が微粒化へ及ぼす影響について検討した．さらに，数値解析を用いて簡易にスワールインジェクタの平均粒径を算出する手法を提案した．ここでは研究の取り組みとその結果ついて簡単に紹介する．実験手法や数値解析手法，詳細な結果と考察については著者らの論文（吉村他，2015）を参照いただきたい．

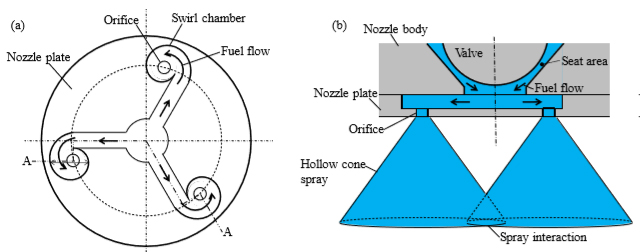
Fig. 1  Schematics of multi-swirl injector. (a) Nozzle plate with three swirl chambers and orifices. (b) Section A-A of injector tip. The fuel is sprayed from the orifice, and hollow cone sprays interact with each other under the orifices.

2.　噴霧干渉が微粒化に及ぼす影響の検討

　本研究では単孔もしくは3孔のノズルプレートを備えたインジェクタを用いて，噴霧の撮影と噴霧液滴の平均粒径であるSauter mean diameter (SMD)の測定を行い，多孔スワールインジェクタの噴霧干渉が微粒化に及ぼす影響について検討した．噴霧撮影ではガソリンの代替燃料としてLow Aromatic White Spirit (LAWS)を用いた．噴霧は大気圧下で測定し，噴射差圧（ΔP_inj）を100 kPaから900 kPaまで変化させた．図2は単孔ノズル，図3は3孔ノズルの噴孔出口近傍における噴霧の様子である．図2より，噴射直後は円錐状の液膜が形成されており，燃料の速度（噴射差圧）が増大するにつれて気液界面の不安定性も増大し，液膜から液滴への分裂が促進されている様子が確認できる．図3の3孔ノズルでは各噴孔からの噴霧が互いに干渉しており，100 kPaと300 kPaでは噴霧の中心部で液膜部分が干渉している様子が確認できる．900 kPaでは噴霧干渉時にはすでに液滴になっており，干渉部の様子は明確ではない．

ΔPinj = 100 kPa	ΔPinj = 300 kPa	ΔPinj = 900 kPa
Fig. 2  Images of spray from injector with the single orifice taken by long-distance microscope. The liquid film is formed under the nozzle and broke up into droplets. The liquid film length is shortened as the injection pressure increased.

ΔPinj = 100 kPa	ΔPinj = 300 kPa	ΔPinj = 900 kPa
Fig. 3  Images of spray from injector with the three orifices taken by long-distance microscope. The spray from each orifice interacts in every condition of injection pressure. In particular, liquid film collisions are seen at 100 kPa and 300 kPa.

　図4は平均粒径の測定結果である．噴霧観察結果と比較すると，噴霧が液膜の状態で干渉している低圧側では単孔ノズルよりも3孔ノズルの平均粒径が大きく，液膜分裂後に干渉している高圧側ではその差が小さい．詳細な考察については論文（吉村他，2015）を参照いただきたいが，噴霧干渉時の燃料の状態（液膜または液滴）と，測定された平均粒径の値には相関があることが確認できる．

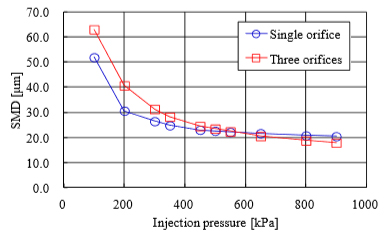
Fig. 4  Measured SMD as a function of injection pressure. The results show that the values of the three orifices are higher than those of the single orifice at a low injection pressure condition. It is considered that the SMD is related to spray interaction.

3.　平均粒径算出手法の提案

　 上記検討で得られた知見を踏まえて，スワールインジェクタによる噴霧の平均粒径を，簡易に算出する手法を提案した．Miyamotoら(Miyamoto et al., 1996)により提案されている環状液膜流の分裂のモデル化による平均粒径の算出式を修正し，スワールインジェクタの噴霧に適用したものである．提案手法では噴孔出口からどの程度下流で液膜が分裂するかを考慮することで，予測精度の高度化を図った．平均粒径の算出に必要な値はノズル内部の気液二相流の数値解析により求めた．

　まず数値解析について紹介する．気液界面形状を捉えるために，解析手法にはvolume of fluid methodを用いた．図5は数値解析に用いた単孔ノズルと3孔ノズルのメッシュであり，インジェクタのバルブ近傍からノズル出口近傍を計算領域とした．図6は解析結果である。旋回室内で壁面に沿った旋回流が生じており，ノズル内部に空気が入り込んでいる．これは旋回室内の旋回流によって遠心力が発生し，旋回の中心側が低圧となったためである．この影響により，噴孔内では壁面に沿った液膜が形成されている．

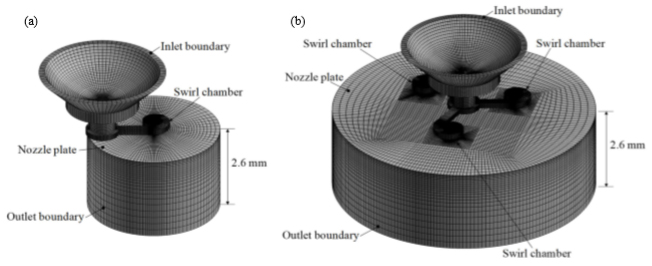Fig. 5  Analysis models with (a) the single orifice and (b) the three orifices. The total number of cells is (a) 0.47 million and (b) 1.39 million.

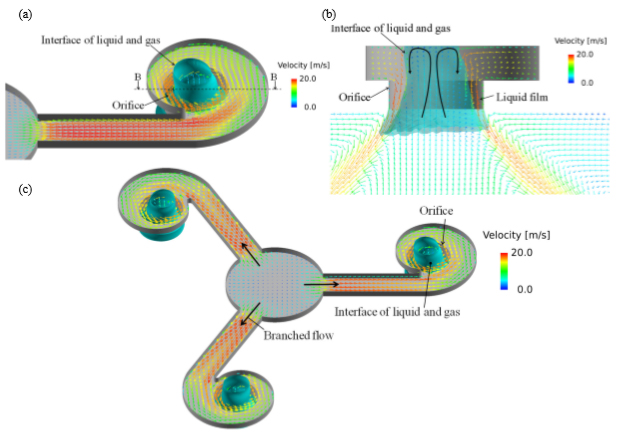
Fig. 6  Visualization of velocity vectors and gas-liquid interface near the orifice with (a) the single orifice, (b) section B-B, and (c) the three orifices. Air penetrates into the swirl chamber because of the pressure drop caused by swirling flow in the nozzle.

　次に，本研究での粒径算出方法について紹介する．Miyamotoら(Miyamoto et al., 1996)は噴孔出口において液膜が分裂すると仮定し，噴射する液膜の厚さhと，気液の相対速度Wを用いて式(1)により平均粒径を算出している．

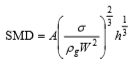(1)

ρ_gは気相の密度，σは表面張力である．式(1)はWeber数の形を用いて整理され，次式のように表すことができる．

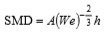(2)

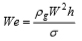(3)

本研究で対象としているスワールインジェクタでは空気の速度が燃料の噴射速度よりも十分遅いこと，噴孔から噴射後に液膜が円錐状に広がるために下流ほど液膜が薄くなることを考慮し，式(2)，(3)を以下のように修正した．

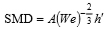(4)

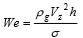(5)

h’は液膜が分裂する時点での液膜厚さ，V_zは燃料の噴孔軸方向速度である．式(4)，(5)の未知の値はV_zとh，h’である．Aは定数であり，任意に設定されるAの値によって算出される平均粒径の値は変化する．本研究では実験結果に基づいて設定した．次に，h’の算出方法について説明する．図7に示すように，噴孔出口面と，噴孔出口面からLcosθ下に位置する平面において，流量が保存されかつ流速が等しいと仮定すると，リング状に形成される液膜断面の面積について，次式が成立する．

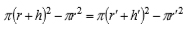(6)

ここで，r，r’は次式で定義され，図7に示すように噴孔出口における気相部分の半径と，液膜長さLの位置における噴霧位置の半径を意味する．

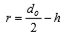(7)

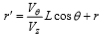(8)

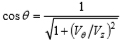(9)

d_oは噴孔出口径である．式(7), (8), (9)を式(6)に代入すると，液膜長さLの位置における液膜厚さh’は次式で表される．

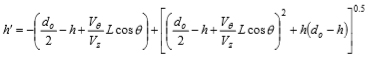(10)

液滴への分裂長さLBUは，Hanら(Han et al., 1997)による円錐状液膜の分裂の式を用いて求めた．

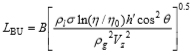(11)

式(11)は Hanらの式の液膜厚さに対してh’cosθを代入した形になっている．ηは液膜分裂時の波の振幅，η₀は初期擾乱の振幅であり，ln(η/η₀)はReynolds数によって異なる(Clark and Dombrowski, 1972)．B は定数である．本研究では噴射差圧によらず，Hanらが使用している値であるln(η/η₀) = 12, B = 3をそのまま用いた．液膜長さLと分裂長さL_BUが等しいと仮定し，式(10)，(11)を解く事で，液膜分裂時の液膜厚さh’を求めることが出来る．h, V_z, V_θは数値解析の結果から，噴孔出口における平均値を与えた．

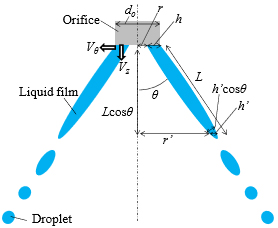
Fig. 7  Schematic of hollow-cone spray and variables used in calculating value of SMD.

　図8 (a)に単孔ノズル，(b)に3孔ノズルの平均粒径(SMD)の実験値と，提案手法による算出値を示す．液滴への分裂長さを考慮した式(4)の影響を確認するために，従来手法である式(2)を用いて計算した値も併せて示している．図8 (a)より単孔ノズルにおける算出値は，分裂長さを考慮することで，低圧側でも実験値とよく一致していることが分かる．図8 (b)の3孔ノズルでは，低圧側で実験値よりも算出値が小さくなる傾向が見られた．実験では噴霧干渉時に液膜が合体して厚くなり，生成される液滴が大きくなったためである．以上より，本研究の粒径算出手法は液膜状態での噴霧干渉が生じない範囲において，多孔スワールインジェクタの平均粒径を精度よく予測可能であることが分かった．

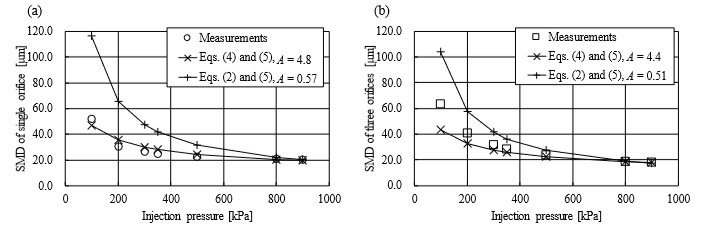
Fig. 8  Comparison of measured SMD and calculated mean droplet diameter with eqs. (2) or (4) in (a) a single orifice and (b) three orifices. The present results are in good agreement with the measured SMD of the single orifice. However, the present results of the three orifices have a gap from measurements at a low injection pressure condition because liquid film collision is not modeled in our study.

4.　おわりに

　本研究は多孔スワールインジェクタによる噴霧の微粒化に関し，噴霧の可視化および平均粒径の測定から噴霧干渉が微粒化に及ぼす影響を明らかにした．さらに，気液二相流の数値解析を用いて噴霧の平均粒径を簡易に算出する手法を提案した．本研究が微粒化技術の発展に少しでも寄与できれば幸いである．

文　　　献

Clark, C. J. and Dombrowski, N., Aerodynamic instability and disintegration of inviscid liquid sheets, Proceedings of the Royal Society of London A, Vol. 329 (1972), pp. 467-478.
Han, Z., Parrish, S., Farrell, V. P. and Reitz, D. R., Modeling atomization processes of pressure-swirl hollow-cone fuel sprays, Atomization and Sprays, Vol. 7 (1997), pp. 663-684.
Miyamoto, T., Kobayashi, T. and Matsumoto, Y., Structure of sprays from an air-assist hollow-cone injector, SAE Technical Paper (1996), 960771.
吉村一樹，安川義人，石井英二，小林信章，ポート噴射エンジン用多孔スワールインジェクタによる噴霧の微粒化に関する研究，日本機械学会論文集，Vol. 81, No. 831 (2015).