温水キャビテーションにおける熱力学的効果の発現に関する実験的研究
 |
| 伊賀 由佳 東北大学, 古澤 哲平 東北大学 |
はじめに
一般に,物体の形状が等しく,それに対する流れの角度が等しい場合,そこに発生するキャビテーションの体積は,主流圧力と飽和蒸気圧との差圧を主流の動圧で無次元化したキャビテーション数σの値に対して相似則があるとされるが,σの値が同じでもキャビティ体積が異なる場合もあり,そのような状況を引き起こす効果を寸法効果と呼ぶ.寸法効果は,核(流体中の残留気泡や不純物,溶存気体,物体表面粗さ,等)の影響を受け,主流のレイノルズ数 Re が高いほどキャビテーションの発生限界が高圧側へ移動し(Holl and Wislicenus, 1961, Arakeri, 1979, Kato, 1984),また同じσで比較してもReが高い場合にキャビテーションの体積が大きくなる(Keller, 2001)ということが知られている.
一方,常温水を除く多くの流体では,同σで比較して,主流温度T∞が高いほどキャビテーションの体積が抑制されることが知られており,この効果はキャビテーションの熱力学的効果(Stepanoff, 1964, Brennen, 1973, Kato, 1984, Fruman et al., 1999, Franc et al., 2004)と呼ばれている.このキャビテーションの体積の抑制は,キャビテーションの発生に伴い蒸発潜熱が奪われ,局所の温度低下に伴い飽和蒸気圧が低下することにより,蒸発が起こりにくくなることに起因するものと考えられる.熱物性値の関係から,液化天然ガスや液体水素などの極低温流体や,高温水,冷媒などで,それぞれのT∞が高いほど熱力学的効果が顕在化する,すなわちキャビテーションの体積の抑制効果が高くなることが知られている.この効果は,同σでキャビテーションの体積が異なる状況を引き起こすため,広義の寸法効果であるとも言えるが,熱的な影響がなくても発現する通常の寸法効果とは区別して取り扱われることが多い.
T∞が上昇した場合,粘性低下の影響でReは高くなる.よって,その際には,キャビテーションの発生を抑制する効果である熱力学的効果と,発生を促進する効果である寸法効果という,相反する効果が同時に働く可能性があると考えられる.一般に,液体窒素などの極低温流体では核や溶存気体の存在が少ないため,寸法効果は小さく,熱力学的効果が顕在化すると考えられるが,水ではその存在の影響が大きく,結果,寸法効果も無視できないのではないかと考える.Cervone らは,常温水からT∞=70 ℃までの温水を用いた単独翼の実験で,T∞が高いほどキャビテーションが成長するという熱力学的効果と反する実験結果を示した(Cervone et al. 2006).我々は,これは,促進効果である寸法効果が,抑制効果である熱力学的効果に勝った結果であろうと予測している.
本研究では,温水に発生するキャビテーションの熱力学的効果と寸法効果の関係について明らかにすることを目的に, NACA16012単独翼まわりの温水キャビテーションのタンネル実験を行った研究 (伊賀,古澤 (2017))について紹介する.本研究では,T∞を変化させる際に主流速度U∞を一定にした場合と,Reを一定にした場合についての比較を通じ,寸法効果をある程度取り除き,熱力学的な効果を抽出した際のキャビテーションの発生範囲や発生形態の変化を明らかにすることにより,単独翼まわりの流れ場において熱力学的効果が発現しやすい条件について考察している.
2. 実験方法
実験は東北大学流体科学研究所に設置されている高温高圧水キャビテーションタンネル(伊賀, 山口, 2016)を用いて行った.本タンネルでは,室温から140 ℃の主流温度において,キャビテーション未発生状態からスーパーキャビテーションまでの,様々な形態のキャビテーションを発生させることが可能である.
本研究の実験条件,実験方法の詳細は伊賀, 古澤 (2017) に記載している.キャビテーション数σ,レイノルズ数Re,熱力学的パラメータΣ(Brennen, 1973),無次元熱力学的パラメータΣ*(Brennen, 1974)はそれぞれ下式で定義している.
キャビテーション数 : 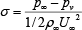 |
(1) |
レイノルズ数 : 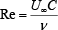 |
(2) |
熱力学的効果パラメータ: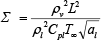 |
(3) |
無次元熱力学的効果パラメータ: 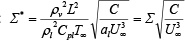 |
(4) |
上式では,U∞,p∞,ρ∞,ν,pvはそれぞれ主流の流速,圧力,密度,動粘度,飽和蒸気圧である.ρv [kg/m3]は主流温度における水蒸気の密度,L [J/kg]は潜熱,Cpl [J/(kg・K)] は水の定圧比熱,αl [m2/s]は水の熱拡散率,C [m] は翼弦長である.σが小さいほどキャビティが発生しやすく,Σが大きいほど熱力学的効果が発現しやすい流れ場である.また,Σ* は熱移動に要する時間を考慮した熱力学的パラメータである.
3. 主流温度30 ℃でのキャビテーション発生形態
主流温度T∞ = 30 ℃,主流速度U∞ = 13.4 m/sにおいて,迎角αとキャビテーション数σを変化させると, 5種類の形態が観察された.それら5種類のキャビテーションの様相を瞬間写真で図1 (a)から(e)に示す.付着シートキャビテーションでは,シート状のキャビテーションが翼負圧面に準定常的に付着する(a).シート・クラウドキャビテーションでは,シートキャビティからクラウドキャビティが周期的に放出される(b).スーパーキャビテーションは,翼の負圧面全体をキャビティが準定常的に覆う(c).バブルキャビテーションは,比較的大きな気泡で構成される(d).後方キャビテーションは,翼負圧面の後半部からシートキャビティが発生する(e).
 |
(a) Attached sheet cavitation (α=8°,σ=2.1) |
 |
(b) Sheet-cloud cavitation (α=8°,σ=1.0) |
 |
(c) Supercavitation (α=8°,σ=0.6) |
 |
(d) Bubble cavitation (α=4°,σ=0.4) |
 |
(e) Back detachment cavitation (α=0°,σ=0.3) |
Fig. 1 Aspects of cavitation on NACA16012 hydrofoil (T∞ = 30 ℃,U∞=13.4 m/s). Snapshots of typical aspects of cavitation pattern are shown.
4. 主流温度の影響(主流速度一定の場合)
通常,キャビテーションの熱力学的効果について論じる際には,主流速度一定で主流温度を上昇させて比較することが多い.そこで,U∞ = 13.4 m/s一定条件下でT∞=30 ℃からT∞=70 ℃に上昇させた際のキャビテーション形態マップを図2に比較する.主流温度の上昇により,キャビティの消滅点がα = 4 degと7 deg 以上でわずかに低σへ移動するが,キャビテーションの発生範囲の大きな変化は見られない.また,α =2 deg, 3 degでは,後方キャビテーションがバブルキャビテーションへと形態が変化しているが,その他は発生形態の大きな変化は見られない.これは,70 ℃程度の温水では熱力学的効果は現れないというこれまでの知見と同じ結果である.
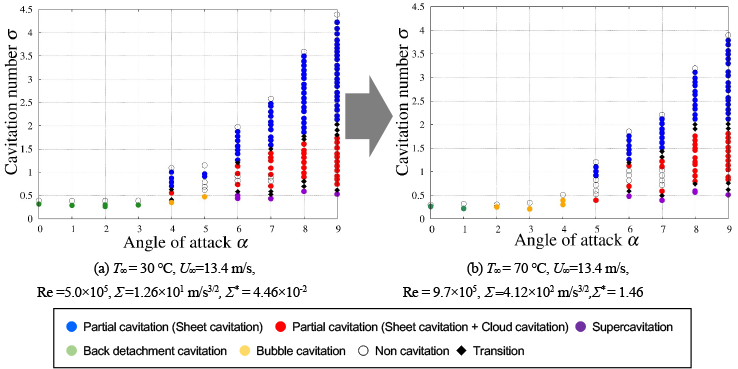
Fig.2 Influence of increase of main flow temperature on occurrence map of cavitation in a condition of constant main flow velocity. The limiting cavitation number was slightly decrease according to increase of main flow temperature to 70 ℃.
5. 主流温度の影響(レイノルズ数一定の場合)
図2の比較では,熱力学的パラメータΣ だけでなくレイノルズ数Reも同時に上昇しているために,熱力学的効果によるキャビティ抑制効果と,寸法効果によるキャビティ促進効果という,相反する2つの効果が重ね合わさり,互いに打ち消しあっているものと予想される.そこで,寸法効果を排除するため,レイノルズ数Re=5.0×105の一定条件下で主流温度を30 ℃から70 ℃に上昇させた際のキャビテーション発生形態マップの変化を図3に示す.図4(a)の30 ℃に対して(b) の70 ℃では,キャビテーションの消滅点が低σへと移動し,発生範囲が抑制されており,特に,図4(b)中に赤枠で示すようにα= 4 degから7 deg の範囲で発生範囲が大幅に抑制されていることがわかる.このことより,寸法効果を取り除き熱力学的効果を抽出すると,主流温度70 ℃程度の比較的低温の温水でも,図3に示すように熱力学的効果によるキャビティ抑制効果は存在することがわかった.
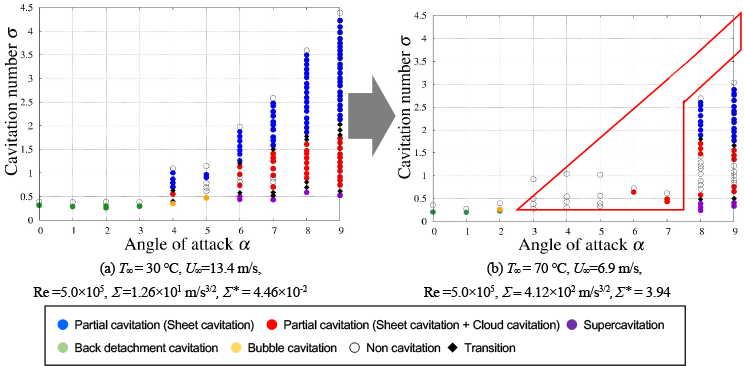
Fig. 3 Influence of increase of main flow temperature on occurrence map of cavitation in a condition of constant Reynolds number. The occurrence region of cavitation was drastically suppressed between angle of attack 4 deg to 7 deg according to increase of main flow temperature to 70 ℃.
また,図3の結果より,翼形では熱力学的効果が特に顕在化する迎角範囲があることがわかる.この迎角の条件については伊賀, 古澤 (2017) で考察している.
6. おわりに
本研究では,レイノルズ数一定条件下で主流温度を上昇させることで,寸法効果の影響をある程度取り除いた状況で熱的な影響のみを抽出することができた.これにより,通常,熱力学的効果は出現しないとされている70 ℃の温水でも,熱力学的効果によるキャビテーションの抑制効果が存在することを示すことができた.また,主流速度一定条件下で主流温度を上昇させた際には,キャビテーションの発生領域は大きくは抑制されなかった.これは,熱力学的効果に加え,レイノルズ数の上昇に伴い,キャビテーションの促進効果である寸法効果も発現し,お互いに打ち消しあった結果であると考えられる.なお,本実験中は,溶存空気量や気泡核数を計測・制御していないが,それらは本研究で得られた結果に大きく影響を及ぼし得ると考えられる.よって,今後,それらを計測または制御した実験を行い,その影響を明らかにする計画である.
文 献
Arakeri, V. H., Cavitation inception, Proceedings of Indian Academy of Science, Vol. C2, Pt. 2 (1979), pp. 149-177.
Brennen, C. E., The dynamic behavior and compliance of a stream of cavitating babbles, Journal of Fluids Engineering, Transaction of ASME, Vol. 95 (1973), pp. 533-541.
Brennen, C. E., Hydrodynamics of pumps, Concepts ETI Inc. and Oxford Science Publications (1974).
Cervone, A., Bramanti, C., Rappo・selli E. and d’Agostino, L., Thermal cavitation experiments on a NACA 0015 hydrofoil, Journal of Fluids Engineering, Transaction of ASME, Vol. 128 (2006), pp. 326-331.
Franc, J. P., Rebattet, C. and Coulon, A., An experimental investigation of thermal effects in a cavitating inducer, Journal of Fluids Engineering, Transaction ASME, Vol. 126 (2004), pp. 716-723.
Fruman, D. H., Reboud, J-L. and Stutz, B., Estimation of thermal effects in cavitation of thermosensible liquids, International Journal of Heat and Mass Transfer, Vol. 42 (1999), pp. 3195-3204.
Holl, J. W. and Wislicenus, G. F., Schale effects on cavitation, Journal of Basic Engineering, Vol. 83 (1961), pp.385-395.
伊賀由佳,山口優貴,高温水中の翼形キャビテーションの内部温度,日本機械学会論文集, Vol.82, No.837(2016), DOI: 10.1299/transjsme. 15-00548.
伊賀由佳, 古澤哲平,温水キャビテーションにおける熱力学的効果の発現に関する実験的研究,日本機械学会論文集, Vol.83, No.845 (2017), p.16-00377.
Kato, H., Thermodynamic effect on incipient and developed sheet cavitation, Proceedings of International Symposium on Cavitation Inception, FED-Vol. 16 (1984), pp. 127-136.
Keller, A. P., Cavitation scale effects empirically founded relation and the correlation of cavitation number and hydrodynamic coefficients, Proceedings of CAV2001, Pasadena (2001), No. lecture001, pp.1-18.
Stepanoff, A. J., Cavitation properties of liquids, Journal of Engineering for Power, Vol. 86 (1964), pp.195-200.

