折れ部を有する曲面の端部から発生するフィードバック音のプラズマアクチュエータを用いた制御

宮本 孟宜， 横山 博史， 飯田 明由　 豊橋技術科学大学

はじめに

　本研究内容は日本機械学会論文集 (2018年84巻861号18-00121) にて発表されたものであり, 光栄にも日本機械学会賞を頂き，また本ニュースレターにて研究を紹介させて頂く機会を頂きました．流体工学部門の皆様に感謝申し上げます．

1.　研究背景

　近年，飛行機や自動車などの輸送機器の高速化に伴い，発生する空力騒音の低減が重要な課題となっている．自動車など輸送機器の車体周りではボンネットのような曲面の一部が折れた形状（図1参照）が多くみられる．このような形状周りの流れでは，曲面に沿って加速した層流境界層が折れ部に流入する場合，流れと音のフィードバックループを伴う強い音が発生する場合がある⁽¹⁾．このような音はフィードバック音とも呼ばれ，狭帯域騒音（ピーク音）であることから聴感上問題となり，発生機構に基づいた低減手法の確立が必要とされている．本研究では，こうした発生音に対しPlasma Actuator (PA) による制御を試みた．PAによる騒音制御メカニズムを明らかにするため，変動する速度と音圧の同時計測結果より発生音に対するCoherent Output Power（COP）分布を風洞実験より評価するとともに，数値計算を行った．

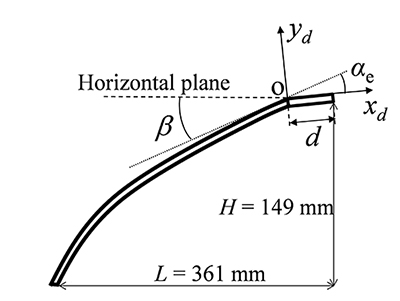
Fig.1  Configurations of flow around a curved plate with a kink shape. The distance from kink to trailing edge was set to be constant of d = 30 mm.

2.　実験・計算条件

　基準となる主流速度U_refは折れ部上20 mmの位置（x_d = 0, y_d/d = 0.67）において測定した流速であり，ここでは強いピーク音が発生したU_ref = 30 m/sの流速の結果を示す．マッハ数はM_ref = 0.088, 折れ部長さdを基準としたレイノルズ数はRe_d = 6.0×10⁵である．折れ部角度はα_e = 9.5°とした．折れ部には加速した層流境界層が流入することを確かめており，高さy_d/d = 0.07程度で流れ方向速度が最大となり主流速度の4%程度加速している．

3.　制御手法

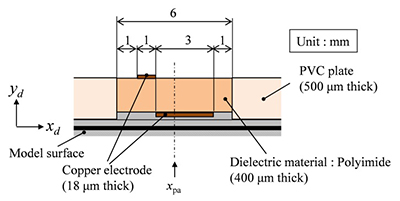
　図2に本実験で使用したPAの形状を示す．PAを設置する際，設置したPAが流れに与える影響を最小限とするため，PAを設置した位置以外のモデル壁面には厚さ500 μmのポリ塩化ビニル（PVC）板を張り，モデル表面に段差ができないよう両面テープなどで調整した．PAの印加周波数はf_pa = 7 kHzとし，ここでは印加電圧をE_pa = 5.5 kV_p-p，PAを折れ部直後（PA中心位置x_pa/d = 0.1）に設置した場合の結果について示す．また，本研究では図4に示すようにPAの時間平均した誘起流の方向が主流と同じ方向となるCo-flowおよび逆向きのCounter-flowの設置条件でそれぞれ実験を行い，効果的なピーク音の制御手法を検討した．

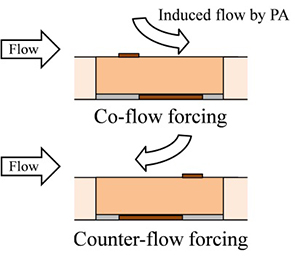Fig.2  Configurations of the present plasma actuator. In this research, the streamwise middle position of the plasma actuator, x_pa, is changed. The actuator is set between polyvinyl chloride (PVC) plates to be flush-mounted. Right figure shows the arrangement of plasma actuator with co-flow and counter-flow configurations.

４.　騒音低減効果

　図3に実験により得られたCo-flowおよびCounter-flowの条件でのPA制御（x_pa/d = 0.1，E_pa = 5.5 kV_p-p）による音圧スペクトルの変化を示す．PA非制御時においてSt = 1.4に発生しているフィードバック音が，Co-flowおよびCounter-flow両方の条件において周囲の周波数のレベルと同程度まで低減されていることがわかる．また制御時ではPAの駆動周波数および風洞の暗騒音の影響が現れるSt < 0.5を除いた周波数の中では，St = 2.3付近でもっとも大きなレベルとなっており，以降ではこの周波数を制御時の基本周波数とする．

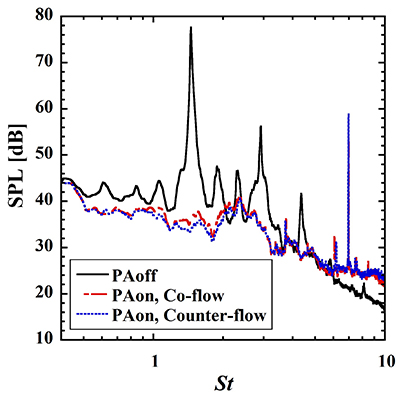
Fig. 3  Measured sound pressure spectra with and without control at U_ref = 30 m/α_e = 9.5º, where the control was performed by the plasma actuator with co-flow and counter-flow configurations at x_pa/d = 0.1 with E_pa = 5.5 kV_p-p. This figure shows that the tonal sound at the fundamental frequency of St = 1.4 was reduced to the floor level by the control with both configurations.

５.　音源への制御効果

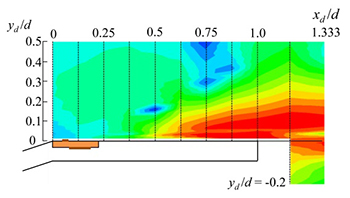
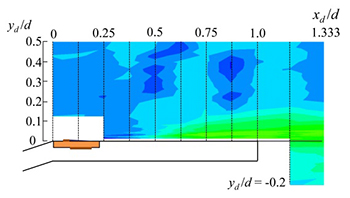
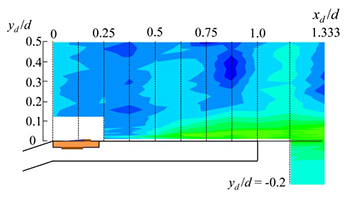
　図4に実験により得られた折れ部周りの非制御・制御時での基本周波数（非制御時 : St = 1.4，制御時 : St = 2.3）におけるCOP分布を示す．図15（a）のPA非制御時の分布より，流れのはく離点付近（x_d/d = 0.25 - 0.375）からCOP値が上昇し，特に再付着点（x_d/d = 0.875 - 1.0）においてCOP値が高い領域が見られる．COPの高い領域は，音圧変動とのコヒーレンスが高くかつ大きなパワーを持った速度変動が生じている領域であり，音の発生に強く寄与している音源と考えられる．また，数値計算結果からも後端近傍において流れの再付着に伴い渦が壁面に衝突することで音波が発生することが確認されている（横山ら，2015）．図15(b)および(c)のPA制御時においても再付着点（x_d/d = 0.625- 0.75）から後端近傍においてCOP値の高い領域が見られるが，非制御時と比較するとその値は大きく低下している．このことは，強いフィードバック音の原因となる二次元的渦構造が制御により抑制された結果と対応していると考えられる．またこのことは数値解析結果からも確認された．

(a) Baseline (St = 1.4)
(b) Controlled with co-flow configuration (St = 2.3)	(c) Controlled with counter-flow configuration (St = 2.3)

Fig. 4  Measured distributions of coherent output power at U_ref = 30 m/s for α_e = 9.5º at fundamental frequency with and without control, where the control is performed by the actuator at x_pa/d = 0.1 with E_pa = 5.5 kV_p-p. (a) The distributions for baseline flow at St = 1.4 are shown. (b) The distributions for controlled flow by the actuator with co-flow configuration at St = 2.3 are shown. (c) The distribution for controlled flow by the actuator with counter-flow configuration at St = 2.3 are shown. These results show that the velocity fluctuations related with the tonal sound is weakened by the control.

さいごに

　自動車などの輸送機関では, 本研究で対象としたようなフィードバック音が車体表面において発生した場合, デザイン性などの観点からボルテックスジェネレータのような意匠の変更を伴う制御手法を採用することが困難です. 本研究ではモデル壁面にフラッシュマウントされたデバイスによる騒音制御が可能であることを示し, 流れのはく離点近傍での制御が騒音低減に効果的であることを明らかにしました. またPAはアクティブなデバイスで入力に対する応答性も優れているため, クローズドループの制御にも適していると考えています. PAは安全性等の課題もありますが，本研究が今後のPAの開発および風騒音制御技術の発展に貢献できれば幸いです.

参考文献

(1)	横山博史, 篠原大志, 中島崇宏, 宮澤真央, 飯田明由, 層流境界層中におかれた折れ部を上流に有する曲面端部から生じるフィードバック音の直接計算, 日本機械学会論文集, Vol.81, No.826 (2015), DOI: 10.1299/transjsme.15-00148.