二次元対向噴流型伸張レオメーターによる平面伸張粘度評価手法の検証
 加藤 学 津山工業高等専門学校  高橋 勉 長岡技術科学大学 |
１．はじめに
伸張粘度は高分子成形加工において加工性や品質に影響を与える重要な物性である．成形加工のなかでも紡糸，フィルム成形，インフレーション成形といった自由表面を持つ流れ場が関係する場合，伸張流動特性がせん断流動特性よりも支配的となる (Morrison, 2001)．伸張流動には，一軸伸張流動，二軸伸張流動，平面伸張流動の三種類があり，それぞれに対して伸張粘度が定義される．三種類の中でも紡糸工程に強い影響を及ぼす一軸伸張粘度は研究の歴史も長く(Koyama, 1991)，複数の一軸伸張粘度用レオメーターが市販されており目的や試料によって使い分けることができる．他方，ブロー成形，フィルム成形，コーティングなどで重要となる二軸伸張粘度や平面伸張粘度の測定手法に関する研究は一軸伸張粘度と比較すると極端に少ない(Kato, Shirakashi, Takahashi 2017)．特に，流動性の高い流体に対応できる汎用的な平面伸張粘度測定技術は開発されておらず市販の測定装置も存在しない．本研究では，精度と汎用性を兼ね備えた新しい平面伸張粘度測定用レオメーターの基本原理を提案し，測定結果から実用性，将来性を考察した(Kato, Takahashi 2017)．
２．機械式・光学式同時測定平面伸張レオメーター
レオメーターは物質の流動特性を明らかにする装置であり，制御された所定の変形（または応力）を与え結果として生じる応力（または変形）を計測する．せん断粘度を評価するには回転式レオメータと同心二重円筒型流路を用いることで長時間にわたり定常なせん断流動場を形成できる．一方，伸張流動場を定常的に発生させることは容易ではなく，その結果として生じる伸張応力を直接計測することも難しい．粘度が高い場合は引張試験のように試料を掴んで引き延ばすこともできるが，流動性の高い流体には適用できない．本研究で提案する装置は，二次元対向噴流のよどみ点において発生する平面伸張流動場を測定領域として，この領域に発生する伸張応力を流動複屈折法で正確に把握し，かつ，対向噴流により発生する反力を機械式に計測してよどみ点での伸張応力を予測する．すなわち，光計測によるよどみ点の局所的で正確な測定と，簡便で汎用的に測定できるが平均的な応力として予測される機械式計測を同時に実行し，双方の利点により欠点を補完できる機械式・光学式同時測定可能な平面伸張レオメーターである．ここでは，本測定手法のポイントとなる試験流体に平面伸張変形を加える方法，平面伸張応力の測定手法さらに伸張速度の求め方について概説する．
2.1 二次元対向噴流による平面伸張流動の形成
Fig.1に示すように2枚の広い平行平板間に対向する矩形ノズルを設置する．ノズルから流出する噴流は平板間に拘束されるため二次元対向噴流を形成する．左右からの噴流は衝突によって上下方向に向きを変え，この際の運動量変化からノズルにはその反作用としてノズル反力Fが作用する．ノズルの中間位置を含むy-z平面上ではFig.1のz軸をよどみ線としてy方向および-y方向に流速が増加し，平面伸張流動場を形成する．平面伸張速度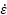
epは，理想流体を仮定したときのx軸上の値を求め，この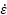epを平面伸張粘度を求める際の値として用いることとした．
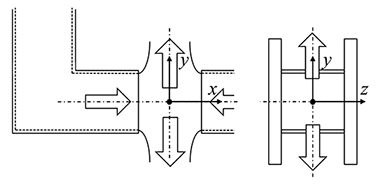
Fig.1 Schematic of planar elongational flow between two-dimensional opposing jets nozzles and its coordinate system.
2.2 平面伸張応力とその測定手法
よどみ線上の正確な平面伸張応力σep_optは得られた流動複屈折Δn'xyから光弾性則を用いて求める．Δn'xyの計測は，レーザー光線をよどみ点に垂直に，(0, 0, z)に沿って透過させ，偏光解析法(Fuller, 1995)を用いて行った．従って，σep_optはよどみ線上の局所的な測定結果が得られる．これに対して，機械式で得られる平面伸張応力σep_mechは，ノズルに作用する力Fをノズル断面積Aで除することで求めた．平面伸張応力は測定領域内の局所的な応力の積分値としてノズルに作用することから，σep_mechは測定領域の全域的な測定結果となる．
Fig.2は，Fを測定する方法を示している．二本のノズルのうち一方（左側）は固定されており，もう一方（右側）はノズルアームと共にアームを保持する支柱を支点として回転可能な状態で保持されている．このノズルアームの他端は荷重変換機につながっており，流動によってノズルに作用する反力はてこの原理により2倍に増幅されて荷重変換機にて計測される．Fig.3に対向ノズルとリザーバー流路の概要を示す．リザーバーにはレーザー光線の偏光状態に影響を及ばさない光学ガラスでできた窓が設けられており，対向ノズルはよどみ点が窓の中央になるように設置する．測定は，対向ノズルが試験流体に完全に沈められた状態を初期状態とし，流量Qをステップ状に立ち上げて，所定の時間流量一定を保ったのち停止させる．この間のFとΔn'xyの立ち上がりと緩和挙動までを計測する．
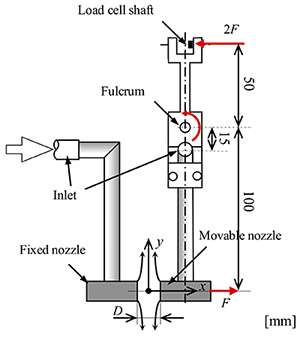
Fig.2 Schematic of two-dimensional opposing jets nozzle device. The left nozzle is fixed and the right nozzle rotates on the fulcrum. The force acting on the movable nozzle is amplified by a factor of 2 due to the principle of leverage. Sample fluid is provided from inlets.
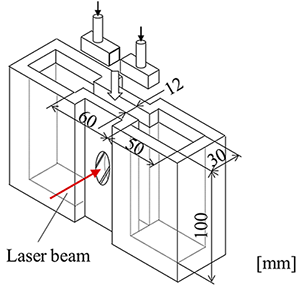
Fig.3 Schematic of the reservoir tank for a simultaneously measurement system. A pair of windows for laser beam transmission is placed at center of the reservoir.
2.3 平面伸張粘度と測定技術の検証方法
平面伸張粘度ηepは算出されたσep_optとσep_mechを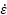epで除することで求まる．また，ηepとせん断粘度ηの比であるトルートン比Trを求める．このように光学式および機械式測定で求めた2つのηepを比較するとともに，異なるηを有する試験流体でのTrの比較を通じ，測定結果の精度や動的特性さらに測定技術の妥当性について検討する．
３．試験流体
本研究では，測定結果を検証するためにNewton流体と粘弾性流体の平面伸張粘度の計測を行った．Newton流体として，水あめ水溶液（75 wt%と80 wt%）を用い，粘弾性流体としてCTAB/NaSal(0.03/0.23 mol/L)界面活性剤水溶液を用いた．CTAB/NaSal界面活性剤水溶液は，低ひずみ速度でせん断粘度が一定となるニュートン域を持ちMaxwellモデルとよく一致する事が知られている．従って，ニュートン域においてTrが4であり，せん断粘度から平面伸張粘度を予測可能である．加えて，光弾性則に従うことから機械式・光学式測定を同時に行うことができることから検証用流体に適した流体である．
４．平面伸張粘度測定結果の検証
4.1 スタートアップおよび緩和における挙動
機械式・光学式同時測定可能なCTAB/NaSal界面活性剤水溶液を用いて，FとΔn'xyのスタートアップと緩和挙動との比較から両者の線形性について確認を行った．Fig.4にFおよびΔn'xyの同時測定結果を示す．縦軸はFとΔn'xy，横軸は経過時間tであり，t=0 からステップ状にQで試験流体の供給を開始し約t=40 s で停止させた．立ち上がりと緩和のいずれにおいても，Δn'xyの方がFよりも僅かに応答が早いことが確認できるが，FとΔn'xyの挙動はほぼ一致している．これは，よどみ点における局所的な測定結果であるΔn'xyとノズル間に作用する平均的σep_mechから誘起されたFとが線形関係にあることを示している．Δn'xyは光弾性則によってよどみ点における平面伸張応力と線形関係にあることから，Fもまた平面伸張応力と線形関係にあり，Fから平面伸張応力が評価可能であることを示している．
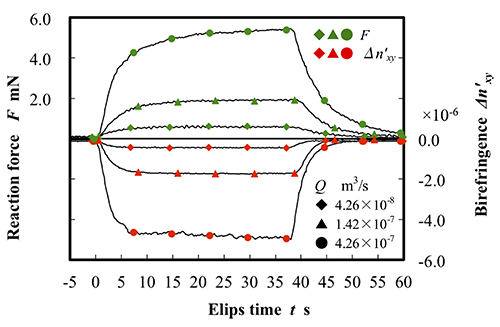
Fig.4 Transient behavior of reaction force and flow birefringence in constant flow rate. They show qualitatively good agreement each other. This result indicates F is linearly related to σep and Δn'xy
4.2 平面伸張粘度評価手法の検証
機械式・光学式手法それぞれで求めたCTAB/NaSal界面活性剤水溶液のηepの比較，さらにせん断粘度から予測される値との比較から評価手法の検証を行った．Fig.5にそれぞれの手法で得たηepと回転型レオメーターで測定したせん断粘度ηとηをMaxwell流体のTr(Tr=4)倍した値を示した．この図より，光学式手法で得られたηepがせん断粘度を４倍した値を示す水平線上に分布し，測定結果が非常に正確な値であることが確認できる．この結果は，伸張速度の評価が光学式手法に対しては妥当であることを示している．一方，機械式手法から得られたηepは，定性的には一定の値を示すものの，定量的には５倍程度大きい値を示す．この光学式手法との結果の違いを理解するために，せん断粘度の異なる流体においてTrを求めその比較を行った．今回測定した３種類の試験流体のTrの結果をFig.6に示す．機械式手法で得られたTrはいずれの流体においても伸張速度に対して独立で，Tr=20程度で一致することが確認できる．このことは，機械式手法においてTr≠4となることが流体のせん断粘度および伸張速度に依存しない要因であることを示している．考えられる主な要因は，機械式測定ではσepをFから式(3)で評価したノズル間の平均的な伸張応力であって，これに対して伸張速度をよどみ点近傍における局所的な値を用いて伸張粘度の評価を行ったためである．これは，ノズル間の速度分布を考慮に入れたより適切な伸張速度の評価をすることで解決可能な問題であり，Trが流体の種類に依存しないことは計測技術としての妥当性を有することを示している．
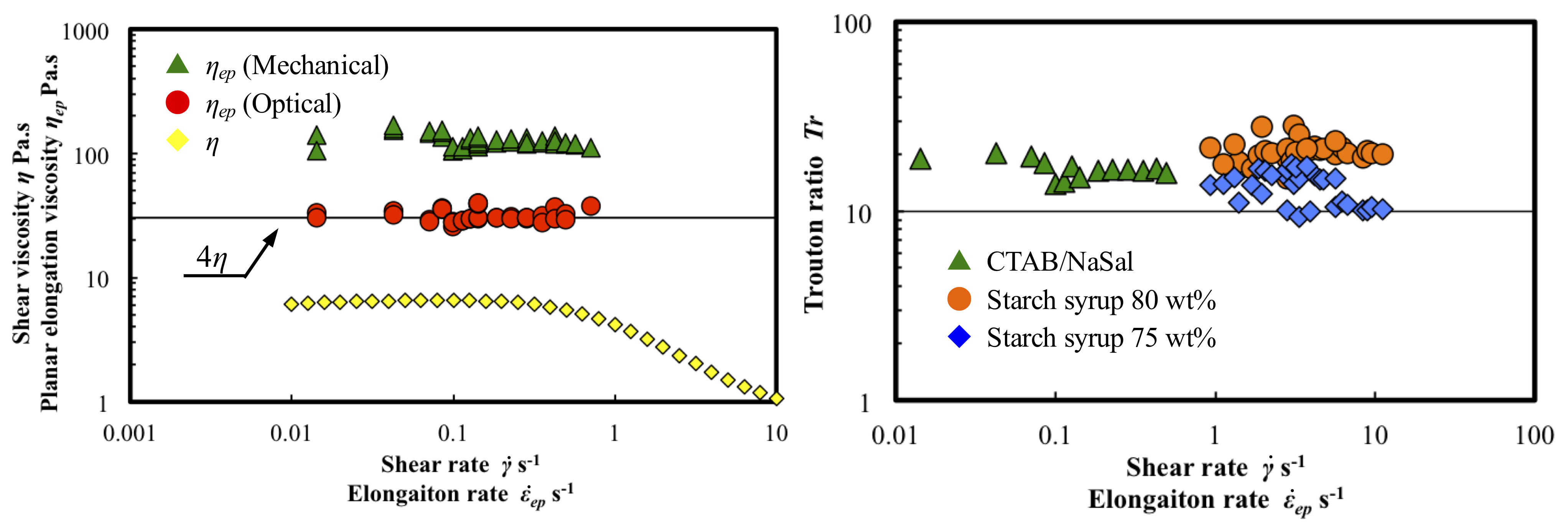
Fig.5 Planar elongational viscosity measured by mechanical and optical techniques. Both results keep a constant value. Optical result coincides with 4 times of shear viscosity.
Fig.6 Trouton ratio of starch syrup aqueous solution and surfactant aqueous solution. They are evaluated from mechanical results. All of Tr show a constant value and they are approximately Tr=20.
５．おわりに
本研究では，光学式手法の精度と機械式手法の汎用性を兼ね備えた新しい低粘度複雑流体の平面伸張粘度を計測する伸張レオメーターの提案を行い，測定結果から本測定技術の検証を行った．測定結果から，光学式手法が適用できる試験流体では高精度な計測が可能であること，さらに，光学式手法が適用できない流体においても，機械式手法の適用により定性的な評価は可能であることを示した．トルートン比が５倍程度高い値となることに留意すれば，現状でも実用上は有益なデータを提供することが可能である．
機械式測定手法に関しては，汎用性を備えた平面伸張レオメーターへの第一歩であり，測定精度を向上させうる検討課題が多く残されている．ノズル間の速度分布を考慮に入れた伸張速度の評価方法の検討はその一つである．加えて，せん断粘度と伸張粘度がひずみ速度に対して一定ではない条件での計測では，平面伸張応力と平面伸張速度の関係はさらに複雑になる．CFDの活用により，ノズルの大きさ，アスペクト比，二次元形状，間隔による速度分布の変化を明らかにすることで，よどみ点の平面伸張速度を用いて平面伸張粘度の評価が可能となる計測条件の検討やより局所的な平面伸張応力を捉える測定技術の検討が重要である．検討課題は残されているものの，本研究を通じて，本測定手法が精度と汎用性を兼ね備えた測定技術になり得る可能性が示された．
参考文献
- Kato, M., Shirakashi, S., Takahashi, T., Measurement of planar elongation stress and viscosity in step planar elongation flow for mobile viscoelastic fluids, Rheol. Acta 56(7-8) (2017), pp.649-659.
- Kato, M., Takahashi, T., Mechanical and optical measurements of planar elongational viscosity with two-dimensional opposing jets nozzle elongational rheometer, Transactions of the JSME (in Japanese), Vol.83, No.849(2017).
- Koyama, K., Studies on Elongational Viscosity of Polymer Melts, Nihon Reoroji Gakkaishi, Vol.19(1991), pp.174-180 (in Japanese).
- Morrion A. F., Understanding Rheology, Oxford University Press, (2001).
- Fuller, G. G., Optical rheometry of complex fluids., Oxford University Press, New York, (1995).