乱れを含む流れの中に置かれた翼から発生する空力音に関する研究
(第 2 報:翼が円柱後流の影響を受ける場合)
 |
 |
 |
| 小林 典彰 大阪大学 |
鈴木 康方 日本大学 |
加藤 千幸 東京大学 |
1.概要
このたびは,2020年度日本機械学会賞(論文)を頂き,大変光栄に思っております.本稿では論文の概要についてご紹介いたします.
本研究では翼から発生する空力音(翼騒音)を対象としており,たとえば,風車の動翼やファンの動翼など翼まわりの流れから発生することが知られています.これらの空力音の発生メカニズムの解明および予測手法や低減手法の開発は工学的に重要な課題であり,従来から多くの研究が行われています(1).さらに,実際に翼が用いられる状況を考えると,たとえば,風車は地形の影響を受ける大気境界層の中に置かれたり,ウィンドファームなどでは風上側の風車の後流の影響を受けたりします.また,空調用のファンでもダクト内に置かれたさまざまな物体により乱れた気流が翼に流入する場合があります.このような状況では発生する空力音が大幅に増大することが知られています(2).したがって,乱れを含む主流中に置かれた翼から発生する空力音も工学的に重要な課題となります.
これまでにも,動的な乱れ発生装置を用いた風洞実験や乱流格子を模擬した数値流体解析を行い,乱れの主要なパラメータである乱れ強度や積分長さスケールが,発生する空力音や翼面の静圧変動に与える影響を調査しました(3).この結果,翼の負圧面前縁近くに,主流の動圧の 6 割程度にもなる大きな静圧変動のピークが生じることがわかりました.このことから,乱れを含む主流中に置かれた翼まわりの流れから大きな音が発生する原因は,翼の前縁近傍の流速や静圧の変動が大きくなることであることが示唆されました.しかし,主流に乱れがある場合に,翼の負圧面の前縁近傍において静圧変動が急激に増大する理由やそのことによりなぜ音が大幅に大きくなるかという点に関しては明らかにすることができませんでした.
そこで本研究では,流れや発生する空力音の特性がよく知られている円柱まわりの流れに着目し,翼の上流側に円柱を設置し,乱れ(カルマン渦列)を生成し,発生する空力音と翼面の静圧変動を風洞実験により調査しました.これは,円柱の後流の流速変動や円柱から発生する空力音はピーク性の変動を有するため,円柱自体により発生する流れの変動や音と,円柱から発生する乱れと翼との干渉効果により発生する流れの変動や音とを分離することができるためです.さらに,円柱の直径や円柱を設置する位置を変化させることにより,翼に流入する乱れの積分長スケールを変化させたり,乱れが通過する位置を変化させたりすることも可能となります.また,Large Eddy Simulation(LES)による数値流体解析(Computational Fluid Dynamics,CFD)により,乱れが翼面に流入した時の渦の変形を詳細に調べるとともに,LES 解析結果を音源とした空力音響解析(Computational Aeroacoustics,CAA)を行い,音場の指向性を調査しました.これらの一連の調査結果により,乱れを含んだ主流中に置かれた翼から発生する空力音が,乱れがない場合と比較して大幅に増大する原因を明らかにしました.以下には,数値解析によって得られた最も重要な結論を示します.
2.数値解析手法
本研究で対象とするのは翼弦長C = 150 mm の二次元形状の対称翼NACA0012です.迎え角は9度,一様流の速度は30 m/sに設定し,翼弦長と一様流の速度により定義される翼のレイノルズ数は3.0×105となります.主流に乱れがない場合,このレイノルズ数における翼まわりの流れは,前縁から翼弦長の5 %程度の位置において,負圧面に短いはく離泡が形成され,10 %程度の位置において,短いはく離泡の崩壊に伴い境界層は乱流に遷移し,遷移した境界層は後縁まで付着することが知られています.圧力面では境界層の遷移は起こらず,圧力面の境界層は淀み点から後縁まで層流となります.翼の上流に設置する円柱の直径は6 mm(翼弦長の4 %)であり,図1のように翼の前縁から100 mm(翼弦長の67 %)上流の位置に設置しました.主流と直交する方向の設置位置に関しては,あらかじめ円柱が無い場合の数値計算を行い,前縁から100 mm上流の位置において,翼の淀み点に流入する流線が通る位置を基準位置(y = 0 mm)としています.円柱の直径と一様流の速度により定義されるレイノルズ数は1.2×104であり,カルマン渦が発生する無次元周波数(Strouhal数)を0.2と仮定すると,円柱から発生するカルマン渦の周波数は1.0 kHzとなります.また,一般に主流に乱れを含む場合は音による流れへのフィードバックが発生することはなく,本研究は主流速度30 m/sの低マッハ数(音速340 m/sにおけるマッハ数0.09)の流れを対象としていることから,非圧縮性流れのLarge Eddy Simulation(LES)により流れ場を求め,次いで,流体音の基礎方程式であるLighthill方程式を用いて音の計算を行う分離解法を用いました.なお,LES計算は翼の負圧面に発達する乱流境界層に対する格子解像度を担保するために,主流速度を20 m/sに設定して実施しました.翼弦長(150 mm)および主流速度(20 m/s)をそれぞれ代表長さ,代表速度としたときの,LES計算のレイノルズ数は2.0×105となります.
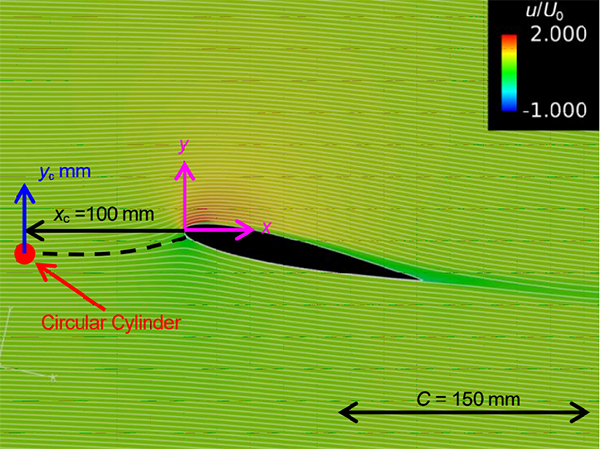
Fig. 1 Computed time-averaged distribution in streamwise velocity around NACA0012 airfoil subjected to wake of a circular cylinder installed upstream of airfoil.
流体解析には,FrontFlow/blue(FFB)を使用しました.FFBはフィルター平均されたNavier-Stokes方程式を時間方向にCrank-Nicolson法(2次精度)で離散化し,空間はガラーキン有限要素法(2次精度)により離散化し,圧力解法には低マッハ数近似を併用したFractional Step法を用いました.LES解析のSub-Grid Scale(SGS)のモデル化にはDynamic Smagorinsky Modelを用いています(4-5).図2に示す解析格子は6面体で作成しており,粘性長さスケールで無次元化した翼近傍の格子解像度はΔx+=20,Δy+=2,Δz+=20となっています.解析領域のスパン方向の長さは翼弦長の5%に設定し,スパン方向には周期境界条件を設定しました.また,下流端の境界を除いた境界面では迎え角に対応する一様流速,下流端の境界では静圧および静圧以外の境界面に作用する力が零となる流出境界条件に設定しました.翼の表面および円柱の表面ではすべり無しの境界条件を設定しましたが,翼面の境界層の有無が翼と円柱後流との干渉効果や発生する音に与える影響を調査するために,翼面のみすべり壁条件を設定した解析も実施しました.また,円柱周りと翼周りの格子は独立に作成しており,オーバーセット法により接続しています.このオーバーセットによる数値的な振動が発生することを避けるために低マッハ数近似を用いています.要素数は翼部(Grid for Airfoil)が約2800万,円柱部(Grid for Cylinder)が約1500万の合計4300万要素です.一方,音響解析には,コンパクトな物体がある場合のLighthill方程式(6-7)の理論解であるCurleの式(8)とFrontFlow/blue-Acoustics(FFB-A)を使用しました.FFB-Aは,Lighthill音源(Lighthillの応力テンソル)の内,運動量の変化量のみを音源として,周波数空間に変換されたLighthill方程式(ヘルムホルツ方程式)をガラーキン有限要素法により離散化して音場を求めます.一般にヘルムホルツ方程式の数値解析では収束性が問題となるため,FFB-Aでは収束性が高いマトリックスソルバーであるIDR法を用いています.本研究では,LES解析により求めた物体(円柱および翼)の流体力変動を用いてCurleの式により空力騒音スペクトルを求めるのとともに,FFBにより計算された瞬時の流れ場(速度)からLighthillの応力テンソルを求め,フーリエ変換したものをFFB-Aに入力し,各周波数における音響解析を実施しました.Curleの式により,円柱から発生するエオルス音など2重極音源が卓越するケースに対して,流体力から簡単に音を求めることができますが,フリースペースのグリーン関数(音場の基本解)を用いているため,翼の後縁から発生する音(後縁騒音)など,物体表面における音の散乱が問題になる場合は適用できません.また,発生する音の指向性を議論することはできません.一方,FFB-Aによる音響解析は,音源データの扱いや計算時間が課題となりますが,音の散乱の影響を取り込むことや,音場の指向性を予測することができます.そのため,本研究ではこれらの二つの方法を併用しました.音響解析の格子は図3のように流体解析格子(Grid for CFD)の外側にさらに拡大した領域をオーバーセットして作成しました.これは,Lighthill音源は速度の2階微分項であるため,マッピングによる内挿誤差を削除するためです.この拡大した領域(Grid for CAA)の要素数は約3300万であり,流体解析部分の格子と合わせて,音響解析の要素数は約7600万要素となります.格子解像度は4 kHzの音波に対して1波長(85 mm)あたり20点(Point per Wave;PPW=20)を満たしています.音響解析の境界条件としては,円柱表面および翼の表面では音響粒子速度を零とし,遠方境界では無反射条件,翼幅方向の境界では周期条件を設定しました.
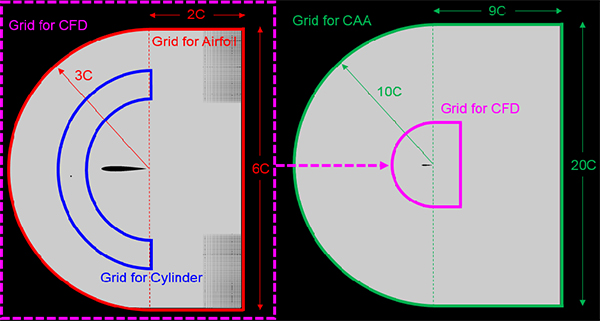
Fig. 2 Computational grids for CFD (left) and CAA (right)
3.結果および考察
3.1.流入した乱れが翼から発生する音に及ぼす影響
図3は翼面がすべり無し条件(no-slip),または,すべり壁条件(slip-wall)に設定した場合において,Curleの式を用いて予測した音圧スペクトルの比較です.ここで,音圧スペクトルは翼の側方(負圧面側)に1 mの位置における値です.また,円柱のみを設置した場合,翼のみを設置した場合の音圧レベルも併記しています.翼のみを設置した場合において,翼面の境界をすべり壁条件にすると,すべり無し条件の場合に比べて音圧スペクトルが広い帯域で低下することが示されています.一方,上流に円柱を設置した場合では,すべり無し条件とすべり壁条件は音圧スペクトルが同程度のレベルであることも示されています.ここで,上流に円柱を設置した場合での音圧スペクトルにおいて,Strouhal数5.0に見られるピークは円柱のカルマン渦に起因するものですが,図3中のStrouhal数の定義に翼弦長(150 mm)を用いているため,円柱の直径(6 mm)を用いたStrouhal数(約0.2)の25倍にピークとなっています.このピーク付近の帯域においては,上流に円柱を設置した場合での翼の音圧スペクトルはすべり無し条件よりもすべり壁条件の方が高いということがわかりました.
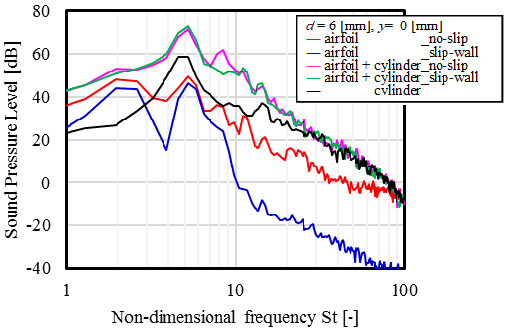
Fig. 3 Comparisons of predicted frequency spectra of sound radiated from flow around airfoil and/or circular cylinder
3.2.翼から発生する音と翼まわりの流れの関係
図4にStrouhal数St = 5.0の音場を示します.前述の通り,この周波数においては,翼の上流に円柱を設置した場合,翼面にすべり壁条件を設定した場合の方がすべり無し条件を設定した場合よりも上流側に放射される音は大きいことがわかりました.翼の表面にすべり壁条件を設定した場合は翼面には境界層が発達せず,すべり壁条件を設定した方がすべり無し条件を設定した場合よりも大きな音が放射されるということは,主流中の乱れと翼面に発達する境界層中の乱れの干渉により音が大きくなる可能性が排除されました.次に,図5に翼の前縁近傍の瞬時の流れの渦構造と静圧分布を示します.翼の上流に円柱を設置しない場合は,前述のように,短いはく離泡の崩壊に伴い,翼の負圧面には乱流境界層が発達していることが示されています.一方,翼の上流側に円柱を設置した場合は,円柱後流の渦が 翼の負圧面と圧力面を通過していることが示されています.また,翼の上流に円柱を設置した場合,円柱後流中の渦が翼の前縁に流入した際に流れ方向に引き伸ばされていることも示されています.淀み点に流入する流線上では,淀み点において主流の速度は零ですが,その後,流線は負圧面側と圧力面側に分岐し,それぞれの流線上において主流は加速しています.つまり,翼まわりに流入した主流中の渦は,淀み点においてアンカリングされ,その後,主流が加速されるため,大きな渦の引き延ばしが生じることが示されています.このことが,乱れを含む主流中に置かれた翼から発生する音が急激に大きくなる本質的な理由となります.つまり,翼面にすべり無しの境界条件を設定した場合よりも,すべり壁条件を設定した場合の方がSt = 5.0の周波数において大きな音が放射された理由は,すべり壁条件の方が主流の加速が大きいからということです.
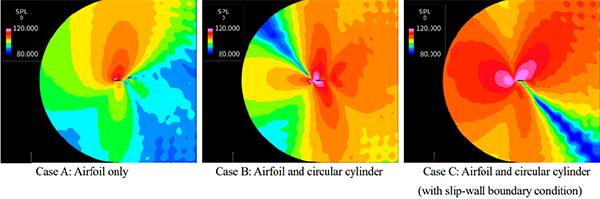
Fig. 4 Computed sound fields at Strouhal number of 5.0 radiated from flow around airfoil (left: Case A) and that around airfoil and circular cylinder (middle: Case B and right: Case C)
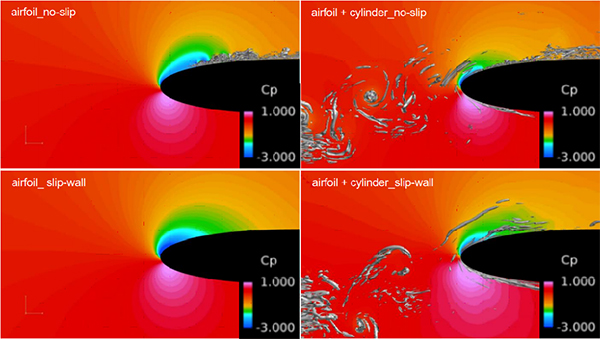
Fig. 5 Computed voritical structures and static-pressure distributions of flow around airfoil for cases with airfoil only with no-slip boundary condition on airfoil surface (top left), with airfoil and cylinder with no-slip boundary condition both on airfoil and cylinder surfaces (top right), with airfoil only with slip-wall boundary condition on airfoil surface (bottom left), and with airfoil and cylinder with no-slip boundary condition on cylinder surface and slip-wall boundary condition on airfoil surface (bottom right)
4.まとめ
本研究では,乱れを含む主流中に置かれた翼まわりの流れから発生する音は乱れがない場合と比べて大きくなる理由を明らかにすることを目的として,LESによる数値流体解析および空力音響解析を行いました.
その結果,乱れが翼の前縁近傍を通過するときに,淀み点においてアンカリングされた渦が主流の加速に伴い流れ方向に引き伸ばされることが,主流に乱れを含む場合に翼まわりの流れから発生する音が大きくなる本質的な原因であることを明らかにしました.
謝辞
豊橋技術科学大学機械工学系の飯田明由教授には音響解析を実施する上で多大なご助言を頂きました.ここに深く感謝の意を表します.

