気泡流中の圧力波を記述する非線形波動方程式の理論的研究
 |
| 金川 哲也 筑波大学 |
標記題目にて,科学技術分野の文部科学大臣表彰若手科学者賞を受賞いたしましたことから,本コーナーへの寄稿の機会を頂けたと伺っております.流体工学部門の皆様に感謝申し上げます.当該研究の9割程は,紙とペンだけを用いた理論的研究ですが,当該部門関連において,現在この種の理論研究はあまり行われていないと認識しております.その意味で,「今熱い」研究に該当するのかを危惧しましたが,それでも,1節と2節で述べますように,理論的手法の採用自体に解決の糸口がある課題には該当します.本稿では,可能な限り数式を用いず,また過度に厳密性に立ち入らずに紹介させて頂きます.また標記題目は基礎研究ですが,最近取り組んでいる応用研究についても触れさせて頂きます.
1. 気泡流中を伝わる圧力波
液体中において,圧力変動が圧力波(音響波)として伝わるとき,長距離の伝播の結果として蓄積される弱い非線形性が,媒質の散逸性とつりあうと,圧力波が衝撃波に発展することがあります(図1).一方で,気泡が液体中に含まれる気泡流を考える場合,気泡の体積振動に起因する(波の)分散性もあらわれ[1,2],この分散性が先述の非線形性とつりあうと,圧力波は(音響的な)ソリトンに発展します(図1).衝撃波とソリトンは,その性質が著しく異なるため,問い「気泡流中の圧力波は衝撃波とソリトンのどちらに発展するのか?」に答えることは,原子力プラントにおける配管やウォータージェットなど多様な工学応用上重要です.そのため,衝撃波とソリトンの起源としての圧力波の「3性質(非線形性・散逸性・分散性)」の定量的把握が望まれますが,実験とCFDから得られるのは,圧力・密度・温度・速度などの現実概念です.「分散計」が存在しないことからもわかるように,実験的あるいは数値的手法によっては,3性質の求値が不可能といえる現状にあります.
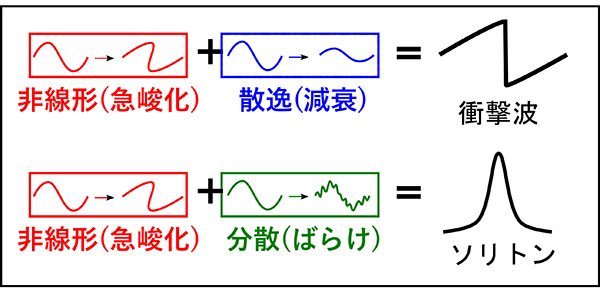
図1: 波の3性質(非線形・散逸・分散)と非線形発展波形(衝撃波・ソリトン).
2. 非線形波動方程式
気泡流に限らず一般に,これら3性質を表現する3項の線形和で表現される非線形偏微分方程式が知られています:
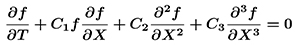 |
( 1 ) |
ここに,各記号は無次元化されており,独立変数のTは時間でXは(1次元)空間座標,未知変数のfは流速や密度や圧力や温度の変動,Ci (i = 1, 2, 3) は係数です.第2・3・4項はそれぞれ非線形項・散逸項・分散項であり,各係数が非線形性・散逸性・分散性の波に対する相対的な寄与の度合いを表します.すなわち,図2に示すように,各係数の大きさを相互に比較することだけで,圧力波の発展波形を大まかに予測することが可能です(厳密には,各係数の比較では不十分で,各項の大きさの比較が必要です).
式(1)は非線形波動論などにおいて周知のKdV-Burgers方程式であり,目新しい式ではありません.非線形散逸分散媒質においては,他にも様々な非線形波動方程式(非線形Schrödinger方程式など)が存在します.(単相)流体中の非線形波動現象に関する代表例として,空気中の衝撃波に対するBurgers方程式(非線形と散逸のつりあい)や,水面波のソリトンに対するKdV方程式(非線形と分散のつりあい)などが,流体力学の基礎方程式系に対する理論近似から導かれ,利活用されてきました.
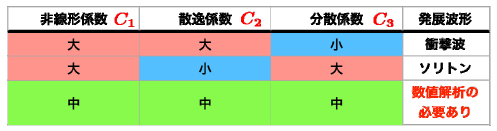
図2: 非線形・散逸・分散の各係数による発展波形の(簡易的)予測.
3. 非線形波動方程式の導出方法
さて,気泡流中の圧力波の伝播においても,KdV-Burgers方程式[2]などの非線形波動方程式が,過去50年以上にわたり導かれてきましたが,その導出は単相流の場合に比べると容易ではありません.気泡流の基礎方程式系(モデル方程式系)は,研究者の数だけ存在するほどに多様であり,そこから導かれる非線形波動方程式も(その係数の関数形も含め)多様極まりないことが困難の一因です.式(1)の散逸係数C2は,単相流であれば粘性係数などから構成される一方で,気泡流の場合には初期条件(気液体積分率や気泡径)や各相の物性値などを複雑に含み,その関数形は基礎方程式系の選定にも依存します.したがいまして,KdV-Burgers方程式1つをとったとしても,単相流とは異なり,相当数の係数が存在するという状況にあります.さらには,特異摂動法など,非線形波動方程式を導くための数学的手法も個々の研究者に依存します.率直に申しますと,筆者個人は,文献[1,2]で行われている導出に関して,数学的には一定の理解はできたものの,物理的な観点からの理解は極めて困難であったことも,当該研究のきっかけの一つでした.
そこで当該研究では,まず,気泡流中の圧力波に対する非線形波動方程式の新たな統一的導出方法自体を構築しました[3,4].これによって,特定の基礎方程式系から多様な非線形波動方程式を導出すること,および,特定の非線形波動方程式を導くために多様な基礎方程式系を採用すること,双方が可能となりました.
その骨格となった考え方は,分散性の(非線形性に対する相対的な)大きさを理論的に規定した点にあります.図3に示す波長と気泡径の大小関係に関する概念図のとおり,長波においては,波から見て,気泡の存在は検知できたとしても,その界面の振動振幅の検知は困難であることがわかります.一方,短波においては,波から見て容易に気泡振動が観測できます.以上を特徴づけるのは,気泡径と波長の比率(無次元比)に他なりません.この考え方を,分散性が気泡の体積振動に起因するという知見[1]と融合すれば,当該無次元数によって分散性の大きさの表現が可能となります.つまり,長波の場合には分散性が高次の補正効果として現れ(気泡径/波長が小さいため分散性が弱い),一方で短波の場合には分散性は補正ではなく主役を演じます(気泡径/波長が大きいため分散性が強い).詳細は割愛しますが,同様に,散逸性の非線形性に対する相対的大きさも無次元数の形に集約することが可能です.
このように,気泡径と波長という現実概念を組み合わせて比率を作ることで,分散性という難解にもきこえる抽象概念の大きさの評価に成功した点が重要です.また,式(1)の非線形・散逸・分散の各係数は,媒質や波の条件(気液の物性値,初期条件,周波数,波長など)の関数であり,これらは実験時に設定するパラメータでもあることから,本理論の実験的実証との親和性を指摘できます.これらのパラメータを変えれば,係数の値が変化し,分散性と散逸性の大きさが変化しますので,分散性と散逸性の制御・増幅・抑制につながり,ソリトンや衝撃波を支配できる可能性も秘めます(その着想は空気中における音響孤立波の形成[5]にあります).これは工学応用上も重要な観点であり,現在,ソリトンと衝撃波の双方を活用した水管の損傷抑制と洗浄の両立を目指す応用研究に着手しています.
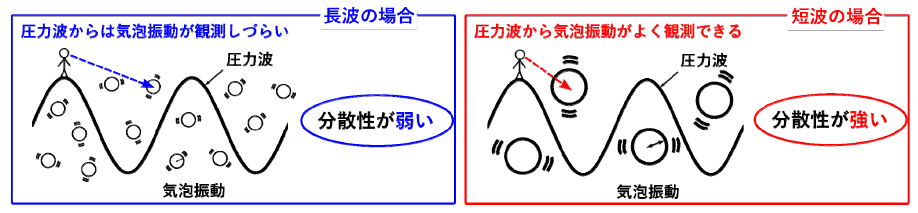
図3: 長波と短波の比較.気泡径と波長の比率による分散性の大きさの評価法[3,4].
4. 医療応用と物理側面の深化
2020年から,応用先の一つである超音波医療に,非線形波動方程式の立場から取り組んでいます.気泡を増強剤的に用いることによって,診断と治療のいずれも,その効率を向上できることが知られています[6].
治療側面においては,マイクロバブル増強型の強力集束超音波による低侵襲腫瘍焼灼術に対する,準一次元の非線形波動方程式を導出し[7],それに基づく数値解析[8]を進め(図4),応用に即した結果を得つつあります.診断側面として,脂質等の膜で覆われたマイクロバブルが現在超音波造影剤に用いられていますが,造影剤の先行理論研究は,いずれも単一(もしくは数個)の気泡を仮定しており,多数の造影剤が投与されるという臨床応用現場からの乖離がありました.そこで,造影剤の集団としての音響特性を表現する非線形波動方程式を導き[9-11],その散逸係数を詳細に調べた結果,膜の圧縮性が超音波を著しく減衰させること[10,11]などが判明しました.
基礎研究の深化にも力を注いでいます.紙数の制約上,直近に発見された物理を3点紹介し,結びとします:(i) 圧力波の研究において過去に見過ごされてきた,気泡に働く抗力を考慮し,抗力が流れのみならず波を散逸させることを指摘しました.抗力による散逸を,粘性・熱・圧縮性による散逸と定量的に比較しました[12-15].(ii) 気液界面における熱伝導とその温度勾配モデルをもとに,熱的効果が上記「3性質」に及ぼす影響を調べました[16,17].(iii) 気泡径の初期非一様分布の定式化を行い[18,19],これが3性質の中でもとくに分散性に大きな影響を及ぼすことを明らかにしました[19].
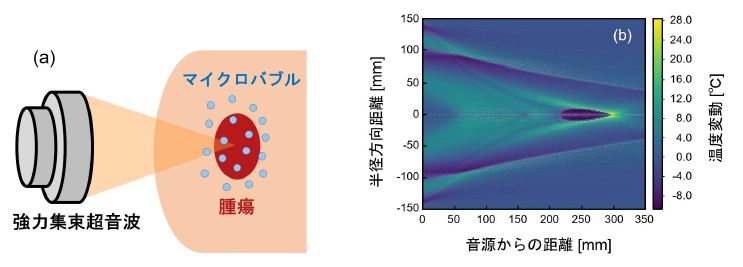
図4:(a) 気泡増強型の集束超音波による腫瘍焼灼術.(b) 非線形波動方程式の数値解(特定時間)[8].
謝辞
3節で述べた理論[3,4]は,筆者が北海道大学博士後期課程在学時,矢野 猛先生(現大阪大学教授),渡部正夫先生(北海道大学教授),藤川重雄先生(現北海道大学名誉教授・流体物理学研究所)のもとで構築したものであり,心からの感謝を申し上げます.4節で述べた内容は,筑波大学金川研究室の学生諸氏と行った成果であり,とくに原著論文[7-19]の共著者である,鮎貝崇広氏,新井秀弥氏,石塚怜央奈氏,加賀見俊介氏,亀井陸史氏,川目拓磨氏,菊地勇成氏,前田泰希氏,本多満洋氏,谷田部貴大氏に,心からの感謝を申し上げます.
本研究の一部は,JSPS科研費(10J03218,12J05892,26820040,16K18008,18K03942,22K03898),NEDO官民による若手研究者発掘支援事業,小野音響学研究助成基金,日本科学協会笹川科学研究助成,カワイサウンド技術・音楽振興財団研究助成,カシオ科学振興財団研究助成,服部報公会工学研究奨励援助金,JKA機械振興補助事業の援助によって行われました.

