乱流境界層における平均速度プロファイルの普遍性とその新たな展開
 |
 |
 |
| 辻 義之 名古屋大学 |
井門 敦志 鉄道総合技術研究所 |
西岡 通男 大阪府立大学 |
このレターでは，文献[1，2]において報告した乱流境界層の速度プロファイルの内容を基に，近年の新たな動向をまとめた．乱流境界層は壁に沿う単純な流れでありながら，多様な物理現象を内在する乱流の複雑さと面白さをそなえており，研究対象として興味が尽きないことが，少しでもお伝えできれば幸いである．
１．はじめに
平板上に一様な速度分布をもつ流れが入るとき，壁では速度がゼロ，壁から十分に離れた高さでは速度が一定となり（主流速度
），平均速度
が連続的に変化する薄い速度境界層が形成される．この平均速度プロファイルを壁からの距離
の関数として表記することは，それほど容易なことではない．高レイノルズ数になり乱流が十分に発達すると，壁から離れたある領域で，平均速度分布が半経験的に導出されている．その速度分布は対数型を示し，式(1)として表記される．
|
(1) |
ここで，上付き添え字＋は内層変数での無次元化（
， 
）をあらわし，
は摩擦速度，
は動粘性係数である．
はカルマン定数と呼ばれ，
となることが，多くの著名な流体力学の教科書に書かれている[3]．しかし，1990年代の後半に，対数速度分布の存在に疑問を投げかける論争がおこり[4，5]，その検証のために高レイノルズ数乱流の実験が盛んにおこなわれた．日本国内からもこの問題にチャレンジしたいと切望しており，長い時間がかかったが，その夢がようやく実現した．
２．大型風洞による実験
対数速度分布は，極めて高いレイノルズ数で観測されるため，対数領域とカルマン定数を定めるには大型風洞での実験が必要となる．本研究では，日本国内の代表的大型風洞として，（公財）鉄道総合技術研究所大型低騒音風洞（以下、米原風洞）において実験をおこなった．その外観を図1に示す．建屋全体が回流式風洞となっており，その大きさは流路中心線の長さが30m×84m，測定部は断面積5m×3m，長さ20mである．測定部流路内に幅5m，長さ20mの平板を設置し，その表面に乱流境界層を発達させ，熱線風速計による速度計測をおこなった．風洞性能の詳細は[6]を参照されたい．新幹線の走行を実現できる300km/h（約83m/s）の風速が優に達成でき，かつ低騒音である．主流速度を
m/sに設定した際に，先端から18.7ｍの位置におけるレイノルズ数は
に達する．諸外国の大型風洞と比べても[2]，米原風洞の実験がいかに高いレイノルズ数を達成しているのかがわかる．
容易に計測できそうな平均速度分布が論争になるのは，多くの計測値にばらつきがあり，統一的な見解が得られないからである．それでは，なぜ，計測値がばらつくほど計測が困難なのか？著者は，その理由が速度そのもの計測にあるのではなく，壁面せん断応力
に基づく摩擦速度
（
）の精度にあると考えている．摩擦速度の精度は，カルマン定数の精度に直結する．つまり，対数速度分布を定めるためには，正確なせん断応力を計測する必要がある．本研究ではオイルフィルム法からせん断応力を算出した[1]．
図１（公財）鉄道総合技術研究所大型低騒音風洞の外観
３．結果および考察
図２には米原風洞で計測した平均速度分布を示す．縦軸と横軸は内層変数で無次元化されている．記号の違いはレイノルズ数の違いを表し，互いに重なる広範囲の対数領域がレイノルズ数の増加とともに，外層に伸びていることがわかる．図中の実線は，式(1)を表す．
実験計測には必ず不確かさが含まれるので，その影響を考慮する必要がある．本計測では，気流の温度変化，キャリブレーション式のフィッテング，熱線の電圧降下，オイル粘度を補正して，1回の計測に対して16通りの速度分布を算出し，同一条件での２度の計測を実施した．平均速度分布の傾きを決定するカルマン定数は，アンサンブル平均として，
， 
であった．対数領域
の外縁は，
であり，対数領域の始まりは
と見積もられた．ここで，
はRotta-Clauser境界層厚さである． 高レイノルズ数乱流境界層において，その平均速度分布には対数速度分布が確かに存在することを確認し，カルマン定数を定めることができた．また，係数
,
の間には，対数領域が微妙に変化しても有意な関係が認められ，外層流れの大きさを特徴づける後流パラメータとも関係することを報告した．
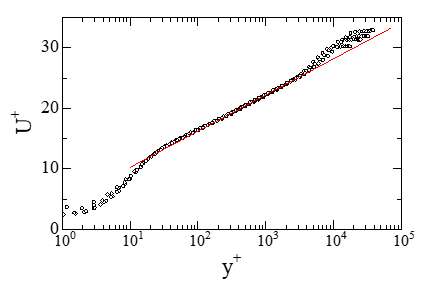
図２ 平均速度分布（平板前縁からx=14.4m 位置で計測）．
.
赤い実線は式（１）をあらわし，
， 
である.
壁に沿う流れは，主流の存在する境界層ばかりではなく，上下が平板のチャネル流れ，周囲を壁面で囲まれた円管流れがある．いずれも，壁に沿う境界層が存在しているが，チャネルや円管流れでは，カルマン定数はいくつになるのか？十分に高いレイノルズ数において，産総研のHi-Ref装置を用いた円管実験では，
が報告され[7]，チャネルについては直接数値計算の結果から
が報告されている[8]．つまり，カルマン定数は，境界層，チャネル，円管流れにおいて同一の値を持つ普遍定数と著者は考えている．
平均速度分布のみならず，変動強度（r.m.s.値）の分布についても対数速度分布が報告されている．流れ方向速度の乱流強度を
として，壁からの距離を境界層厚さ
で無次元化すると，壁からある範囲において，対数則が観測される．
|
(2) |
対数則の物理的背景は，TownsendのAttached Eddy Model[9]によって解釈されている．壁に付着した渦構造が階層的に存在して，その寄与から乱流強度の分布が決まると考えられている．対数則の傾き
（
）はレイノルズ数依性を持つと予想され，渦構造としてVLSM(Very Large Scale Motion)やLSM(Large Scale Motion)の寄与があり，それらが壁からの位置とレイノルズ数によって複雑に変化する．従って，式(2)の真偽性についての決着には，まだ時間がかかりそうである．
より高いレイノルズ数で，平均速度や乱流強度の分布はどうなるのか？著者らが到達したレイノルズ数は，依然として有限である．乱流としての興味はより高いレイノルズ数の極限にある．レイノルズ数無限大の極限で，エネルギー散逸率は有限値をとることが予想されている．もしこの予想が正しければ，壁乱流のエネルギー散逸率も有限値に漸近することが予測される[10]．いま，対数領域内の１点を
として，式(2)に代入すると，乱流強度はレイノルズ数とともに無限に増大する（
， 
）こととなり，散逸率が有限になることと矛盾してしまう．式(2)に代わる新たな式も提案されているが，その検証にはより高レイノルズ数のデータが必要となる．もしかすると，平均速度分布にも，対数則に代わる新たな分布が出現するかもしれない．
量子コンピュータが実現されれば，より高レイノルズ数の乱流を数値実験として理解できるだろう．新たな実験として，極低温下で粘性の極めて小さなのヘリウムを利用する可能がある．超流動を利用した超流動風洞を実現できれば，超高レイノルズ数の乱流を実現できると期待している．
おわりに
共著者の西岡通男先生は，本論文[2]の掲載が決まるとほぼ同じ時期に，ご逝去されました．謹んでご冥福をお祈りいたします．本論文の成果は，日本を代表する境界層データとして世界に公開していきたいと思います．米原風洞での実験は，現地の多くのスタッフの方々，当時の大学院生の協力なしには達成できませんでした．ここに感謝の意を表します．