Bayesian optimization of traveling wave-like wall deformation for friction drag reduction in turbulent channel flow

難波江 佑介 東京理科大学 深潟 康二 慶應義塾大学

1.　はじめに

　2021年12月に部門英文ジャーナルであるJournal of Fluid Science and Technologyに公刊されました我々の論文^[1]に対して，光栄にも2022年度日本機械学会賞（論文）を頂きました．さらに，ニュースレターとして論文内容を紹介する機会も頂きました．この場をお借りして学会賞にご推薦いただきました日本機械学会流体工学部門の皆様に御礼申し上げます．

2. 背景および目的

　流体の粘性に起因する摩擦抵抗低減のための流れの制御手法の確立は，エネルギー問題解決のための最重要課題の1つである．中でも，壁面変形により生成される進行波制御（進行波状壁面変形制御，図1）は，数値シミュレーション^[2,3]および実験^[4]双方で大きな抵抗低減効果が確認された実装に最も近い制御手法の1つである．しかしながら，これらの先行研究では，パラメトリック・スタディによる検証が行われているのみであるため，制御パラメータの最適化は不十分である．そこで，高コスト関数やブラックボックス関数に対する効率的な最適化が可能であるベイズ最適^[5]を用いて，進行波状壁面変形の制御パラメータを最適化し，さらなる抵抗低減効果を得ることを本研究の目的とする．

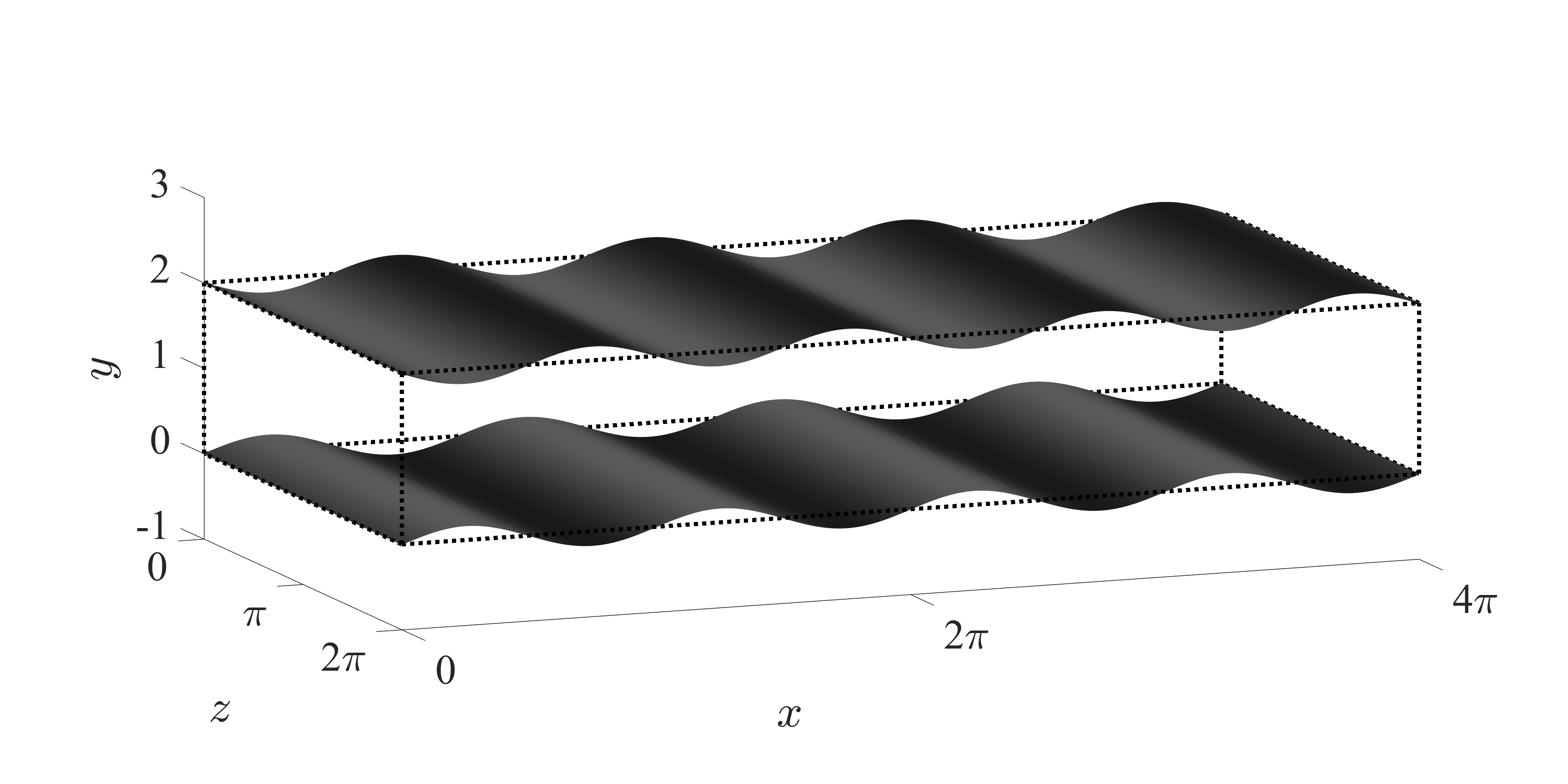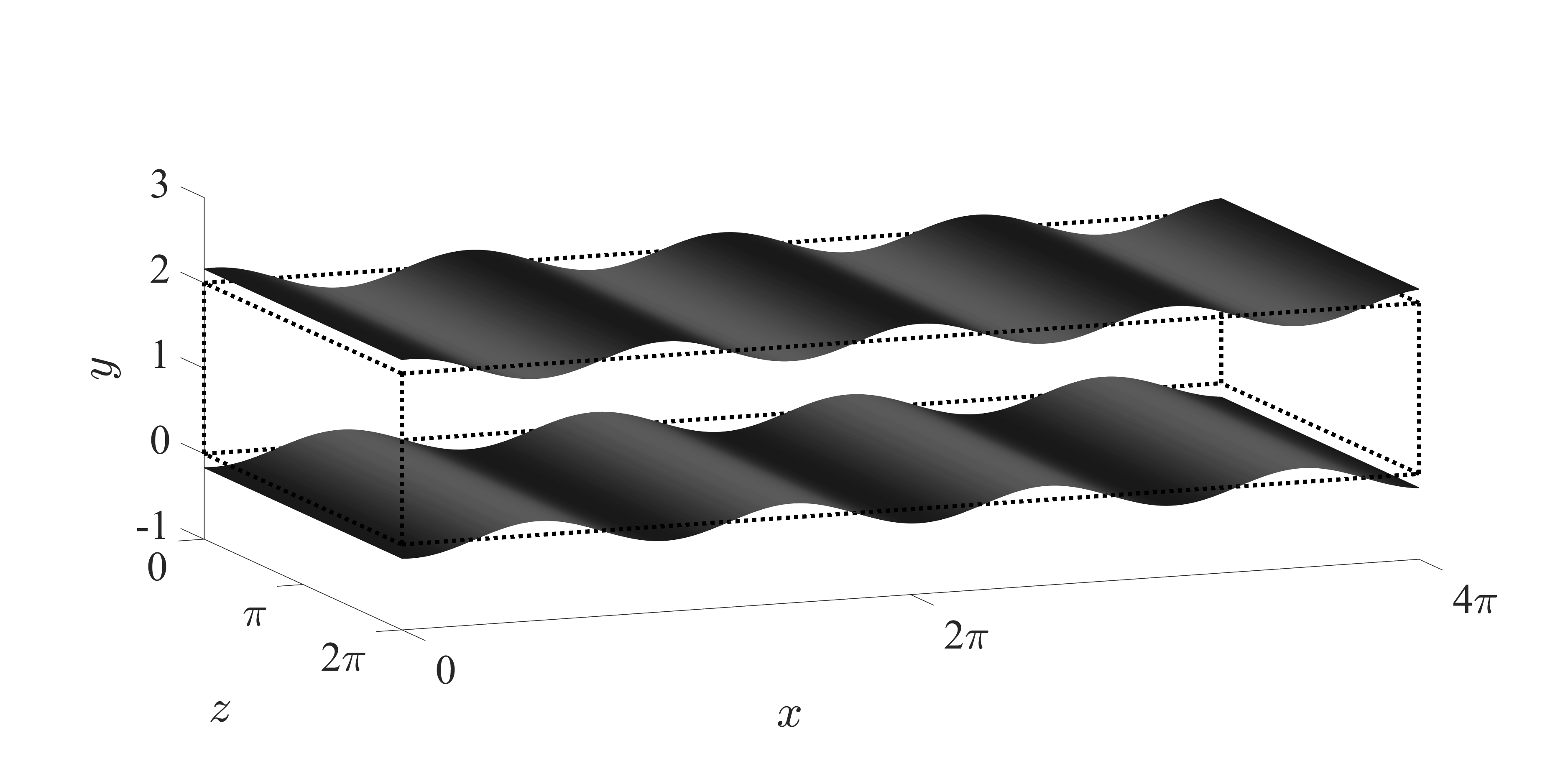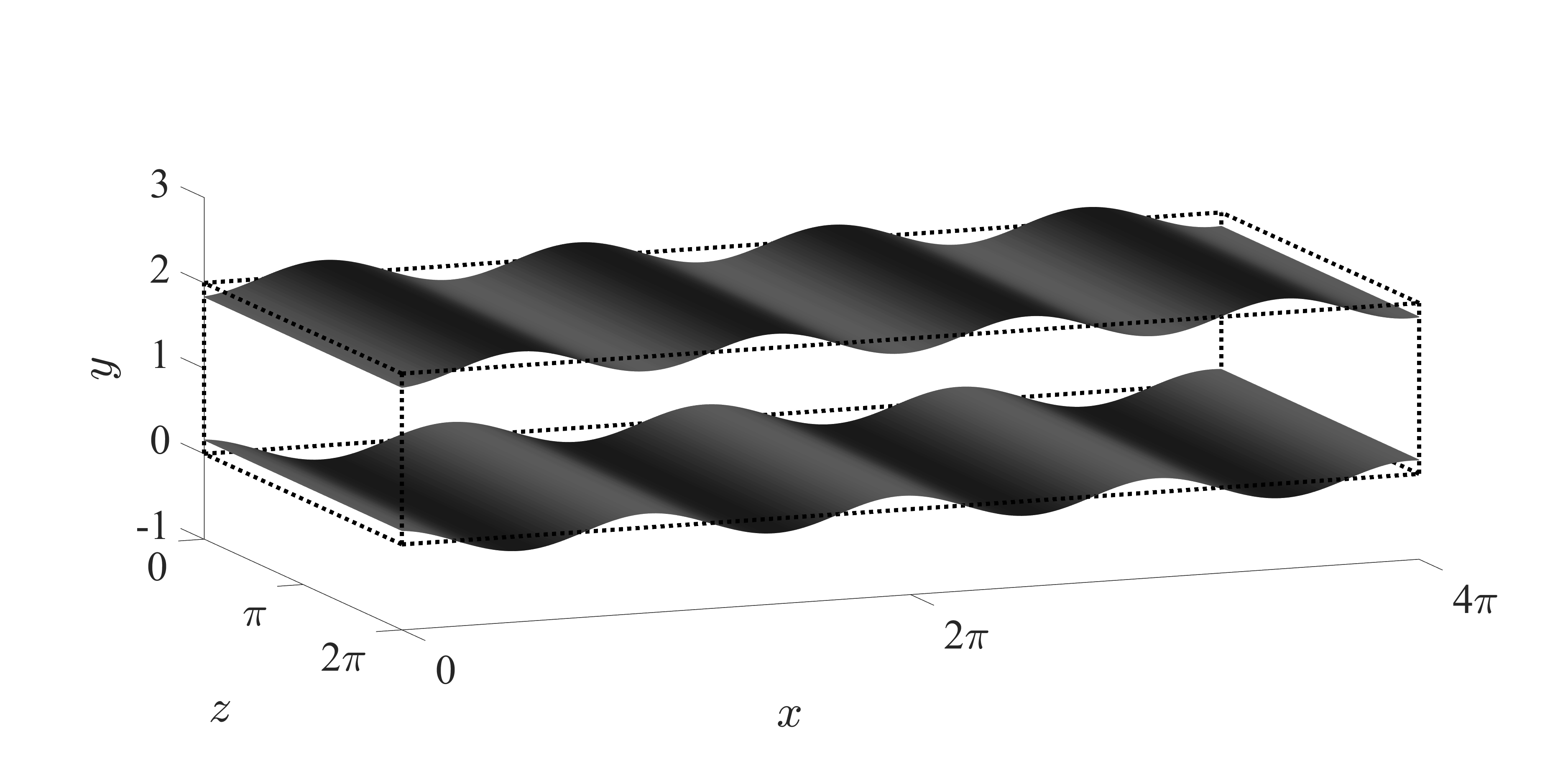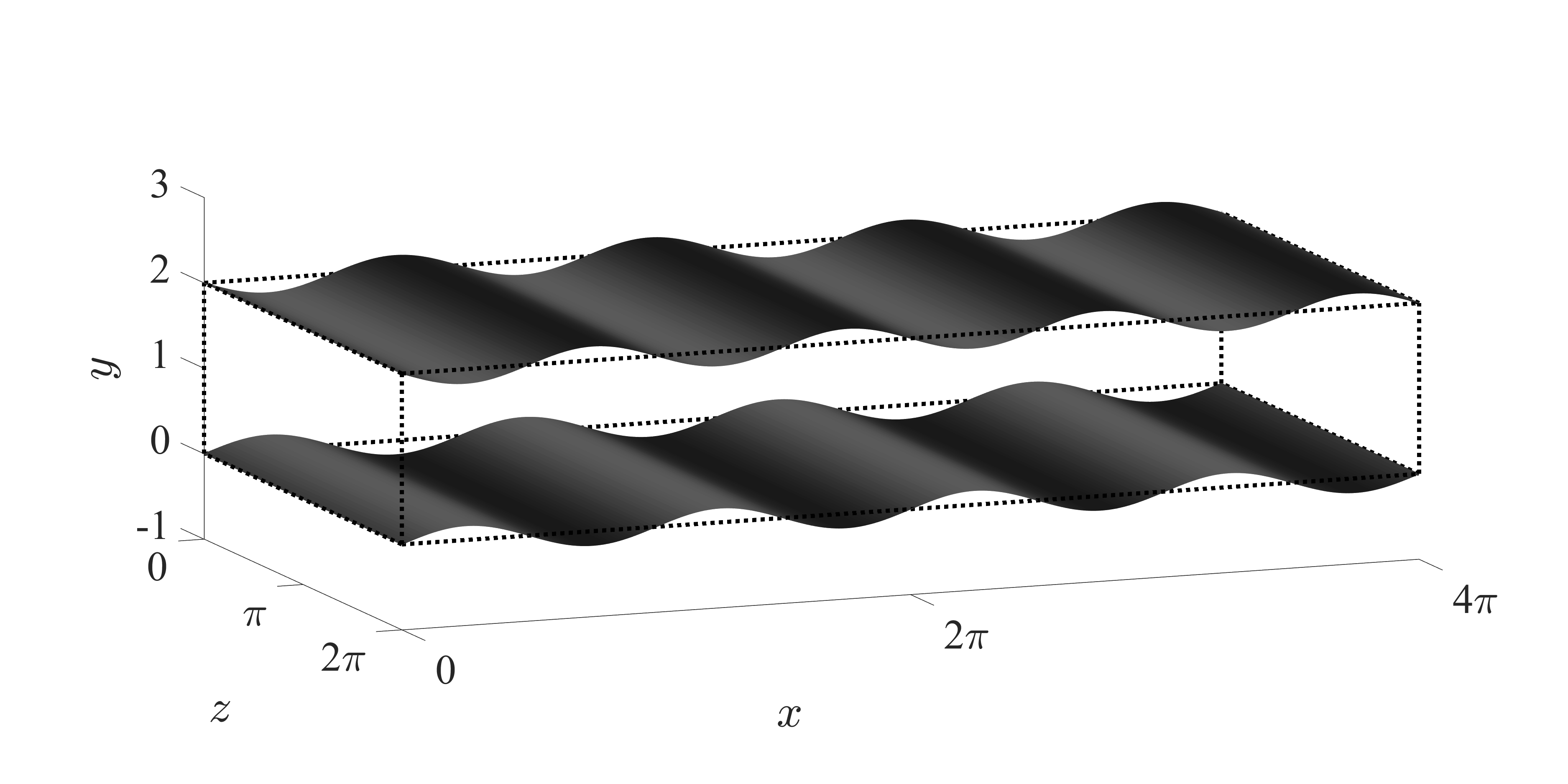
Fig. 1： Schematic of streamwise traveling wave-like wall deformation.

(a)	(b)
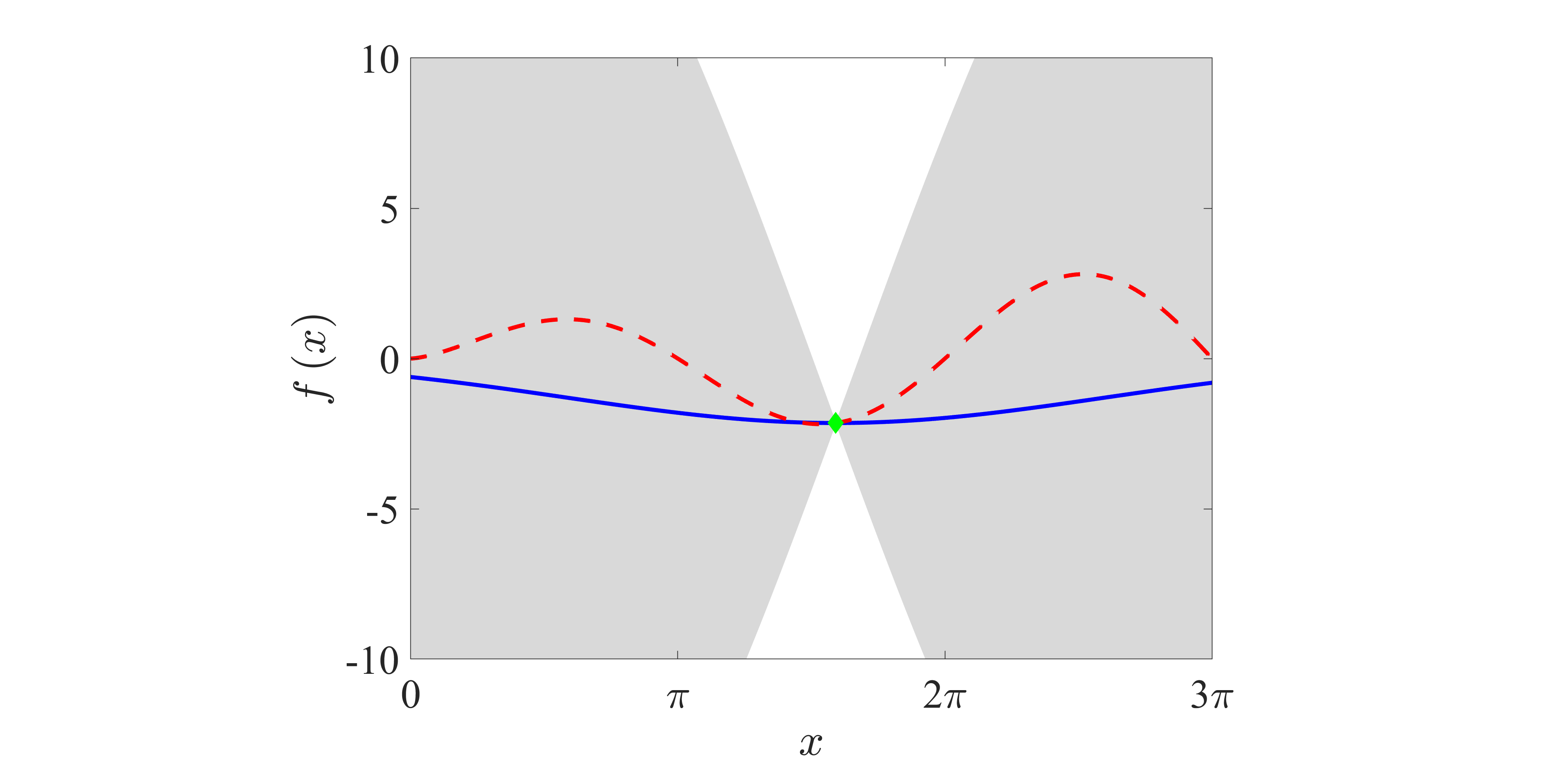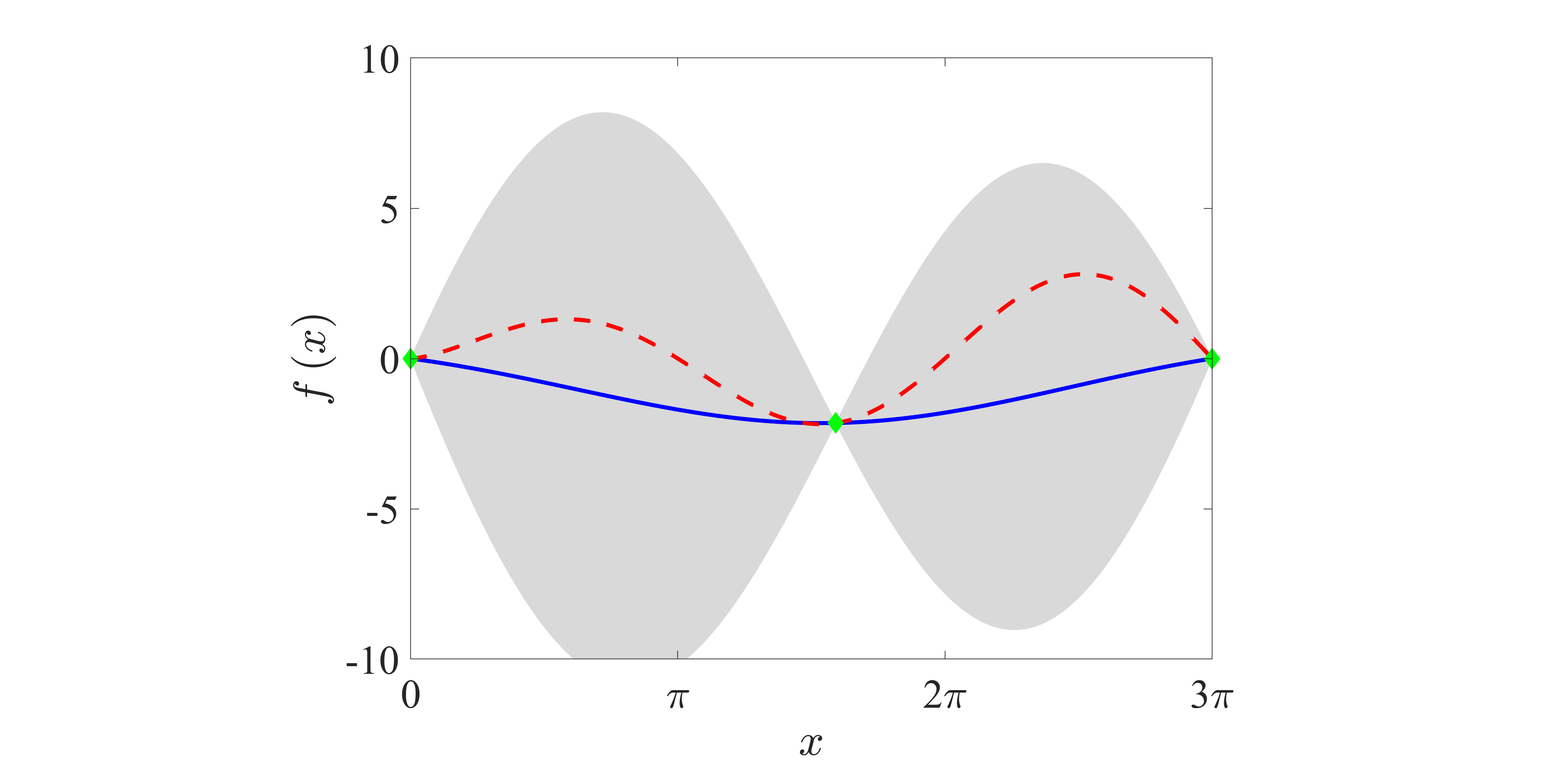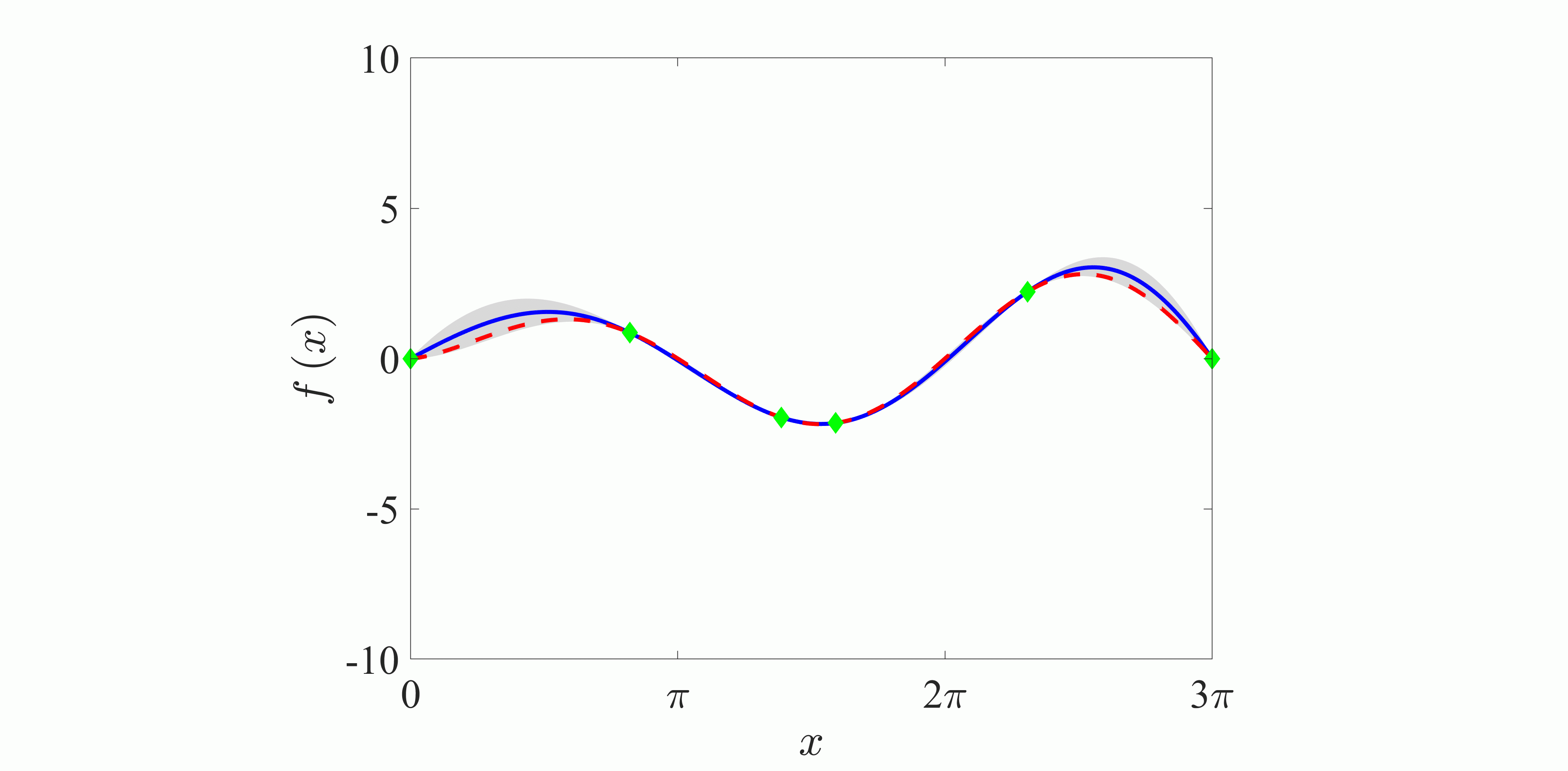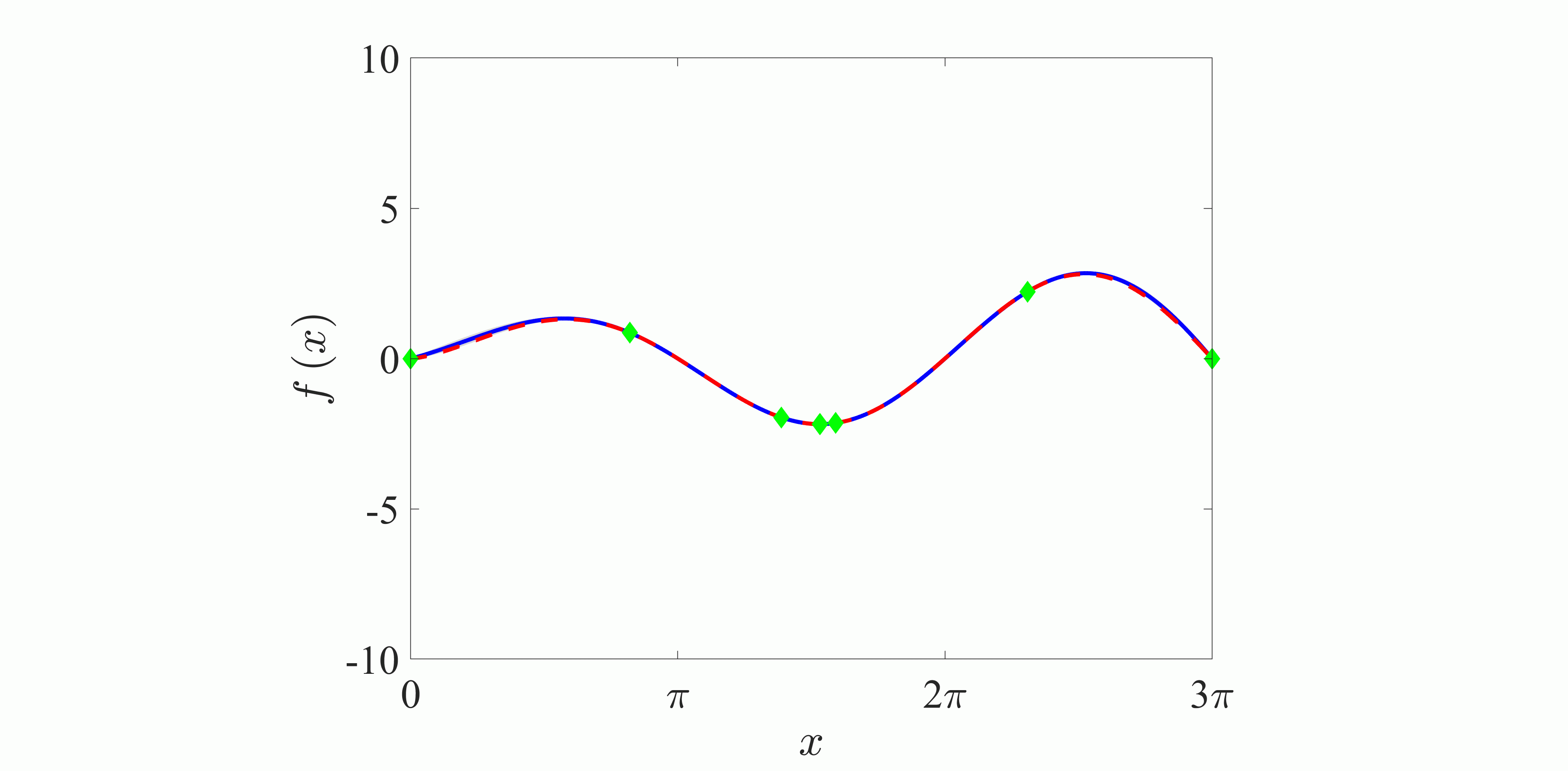
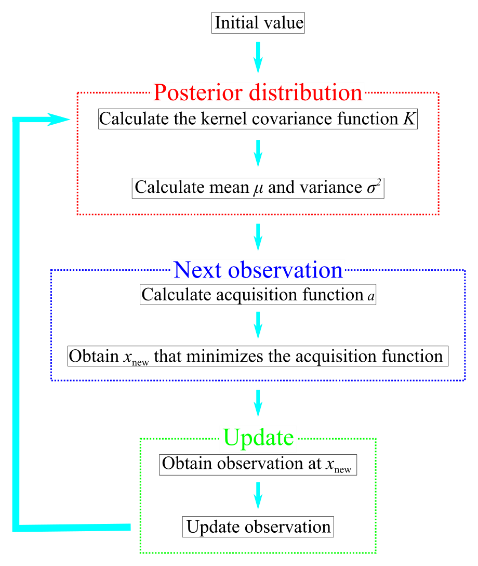
Fig. 2： (a) Schematic chart and (b) flowchart of the Bayesian optimization. In (a), the horizontal axis is the variable x, and the vertical axis is the observation value f(x). Blue line, posterior distribution; gray area, 95% confidence bound; red dashed line, true function; green point, observations.

3. ベイズ最適化

　図2にベイズ最適化の概念図および最適化のフローチャートを示す．ベイズ最適化は，(i)予測分布の算出，(ii)次の観測点の決定，(iii)観測点の更新，の3段階より構成される．ただし，ここでは最小値問題を考える．

　はじめに，ある目的関数の既存の観測点にガウス過程回帰を適用することで，予測分布の平均と分散を算出する．図2(a)において，青実線は平均，灰色領域が平均と分散より算出した95%信頼区間，赤点線が真の関数を示す．

　次に，次の観測点を決定するために，(i)で算出した平均と分散に基づく獲得関数を用いる．獲得関数が最小となる点が次の観測点である．本研究では，信頼区間の最小値を次の観測点とするGP-LCB (Gaussian Process-Lower Confidence Bound)^[6]を用いる．

　最後に，(ii)で決定した観測点における評価を数値計算や実験で行い，得られた結果を既存の観測点に加えて，観測点の更新を行う．これらのプロセスを繰り返すことによって，最適化を実行していく．

4. 結果および考察

　進行波状壁面変形の制御パラメータにベイズ最適化を適用する．本研究では，逆流も考慮可能な最小値問題とするために，抵抗低減率と直結する-U_b（U_bはバルク平均速度）を目的関数とする．また，進行波の波数k_xを固定し，壁面変形速度v_wと位相速度cの最適化を行う．筆者らが実施した直接数値シミュレーション(DNS)によるパラメトリック・スタディの結果^[3]を初期値とし，観測点における評価は，先行研究と同様にDNSを用いて行う．

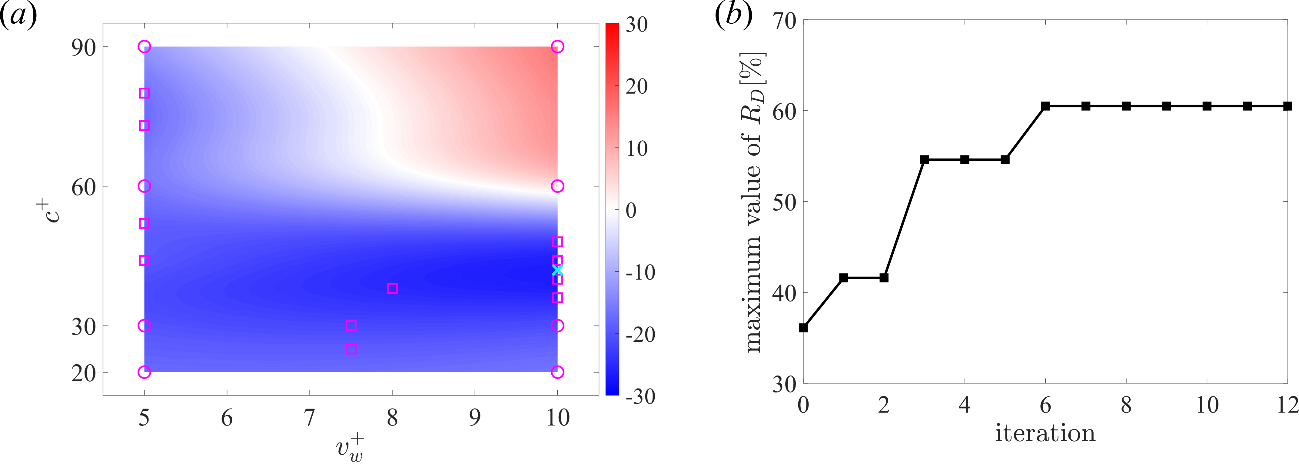
Fig. 3： (a) The mean after 12 updates. (b) The update history of the maximum value of the drag reduction rate RD. In (a), circle, square, and cross denote the initial points, the observation points, and the best point, respectively.

　12回更新後の予測分布および最大抵抗低減率の推移を図3に示す．最適化の結果，周期的な流動変動を許す場合，パラメトリック・スタディによる最大抵抗低減率36.1%をはるかに凌ぐ60.5%の抵抗低減をわずか10回程度の試行で達成した．これらの結果は，制御パラメータの微調整により大幅に抵抗低減効果を向上させることが可能であることを示している．さらに，このような激しい流動変動を伴う場合，制御による層流化と壁面近傍の逆流由来の変曲点が引き起こす不安定性による乱流への再遷移を繰り返すことにより，高い抵抗低減効果が維持されていることが明らかとなった．

5. さいごに

　本研究では，進行波状壁面変形の制御パラメータにベイズ最適化を適用し，先行研究^[3]をはるかに凌ぐ60.5%の抵抗低減が達成された．本研究で得られた知見が，基礎研究から開発研究まで幅広い層に応用され，エネルギー利用の効率化が促進されることを切に願う．

謝辞

　本研究の一部は，科研費(基盤研究(C)25420129，基盤研究(A)18H03758，基盤研究(S)21H05007)の助成を受けて実施されたものです．末筆ではありますが，ご指導いただきました小尾晋之介教授，安藤景太准教授，卒業生の河合謙氏(慶應義塾大学)に深く感謝申し上げます．

参考文献

[1]	Nabae, Y. and Fukagata, K., Bayesian optimization of traveling wave-like wall deformation for friction drag reduction in turbulent channel flow, Journal of Fluid Science and Technology, Vol. 16 (2021), JFST0024.
[2]	Nakanishi, R., Mamori, H., and Fukagata, K., Relaminarization of turbulent channel flow using traveling wave-like wall deformation, International Journal of Heat and Fluid Flow, Vol. 35 (2012), pp. 152-159.
[3]	Nabae, Y., Kawai, K., and Fukagata, K., Prediction of drag reduction effect by streamwise traveling wave-like wall deformation in turbulent channel flow at practically high Reynolds numbers, International Journal of Heat and Fluid Flow, Vol. 82 (2020), 108550.
[4]	Suzuki, I., Shimura, T., Mitsuishi, A., Iwamoto, K., and Murata, A., Experimental study on drag reduction effect with traveling wave control using PIV measurement, Proc. ASME-JSME-KEMS Joint Fluids Engineering Conference 2019, San Francisco, USA, AJKFLUID2019-4855 (2019).
[5]	Brochu, E., Cora, V., and Freitas, N., A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning, arXiv preprint arXiv:1012.2599 (2010).
[6]	Srinivas, N., Krause, A., Kakade, M., S., and Seeger, M., Gaussian process optimization in the bandit setting: No regret and experimental design, Proc. 27th International Conference on Machine Learning (ICML27) (2010), pp. 1015-1022.