Newsletter  2018.1  Index

Theme : "Mechanical Engineering Congress, 2017 Japan (MECJ-17)" Preface M. MOTOZAWA, S. KUROSAWA Research Progress of Functional Fluids Engineering Hideya NISHIYAMA (Tohoku University) Heat transfer enhancement and drag reducing methods inspired by the skin surfaces of dolphins Yoshimichi HAGIWARA (Kyoto Institute of Technology) On the injection depth of the laser-induced microjet into the soft material Nanami ENDO, Sennosuke KAWAMOTO, Yoshiyuki TAGAWA (Tokyo University of Agriculture and Technology) Cavitation onset induced by sudden acceleration Akihito KIYAMA (Tokyo University of Agriculture and Technology), Zhao Pan (Utah State University), Yoshiyuki TAGAWA (Tokyo University of Agriculture and Technology), Jesse Daily (Naval Undersea Warfare Center), Scott Thomson (Brigham Young University), Randy Hurd, Tadd Truscott (Utah State University) Investigation of the sustaining mechanism of turbulence of Newtonian fluids by using viscoelastic fluids Yasufumi HORIMOTO, Susumu GOTO (Osaka University)

 

Investigation of the sustaining mechanism of turbulence of Newtonian fluids by using viscoelastic fluids

Yasufumi HORIMOTO, Susumu GOTO Osaka University

Abstract

On the basis of systematic investigations of the turbulence suppression due to a small amount of surfactant additives, we can obtain important information on the sustaining mechanism of the turbulence. To show that this strategy is useful, we have experimentally investigated turbulence suppression in a precessing sphere. Combining our experimental results with previous theories on the onset of turbulence suppression by viscoelasticity of fluids, we can conclude that the sustaining mechanism of turbulence in the sphere is an energy cascading process starting from the largest-scale vortices in turbulence.

 

Key words

Turbulence, Laboratory experiments, Viscoelastic fluids, Rotating fluids

 

Figures

Movie. 1 Precession of a sphere. The word “precession” denotes the rotation of the spin axis of a rotating object. Precession of a container can sustain developed turbulence of the confined fluid. Flow in the sphere is controlled only by two dimensionless parameters: the Reynolds number, Re=a²Ω_s/ν, and the Poincaré number, Po=Ω_p/Ω_s. Here, a is the radius of the sphere, ν is the kinematic viscosity of fluid, and  Ω_p and  Ω_s are the magnitudes of the angular velocity of the spin and precession, respectively.

 

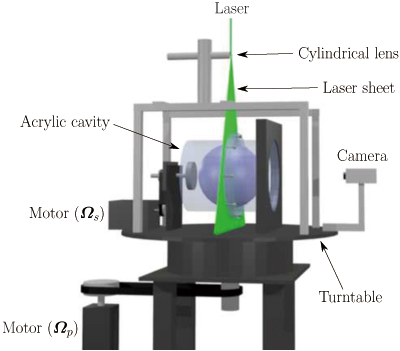
Fig.1 Experimental apparatus. An acrylic container with a spherical cavity is rotated by a motor on a turntable which is rotated by another motor. A laser sheet visualizes flow on the equatorial plane of the cavity so that we can conduct flake visualization and particle image velocimetry (PIV) of the flow. A camera fixed on the turntable records the visualized flow.

 

Movie. 2 Turbulence of (left) water and (right) the dilute surfactant (CTAC) solution. Re=4.0×10⁴, Po=0.1. If the working fluid is Newtonian, e.g. water, and Re is sufficiently high, fully developed turbulence is sustained for Po=O(0.1) ^[1,2], which is the target of this study. When we add a small amount of surfactant to this turbulence, drastic turbulence suppression occurs (see reviews ^[3,4] of turbulence reduction by additives). We investigate this suppressed turbulence to understand the developed turbulence of water, since the suppression is due to the absence of the sustaining mechanism of turbulence ^[5].

 

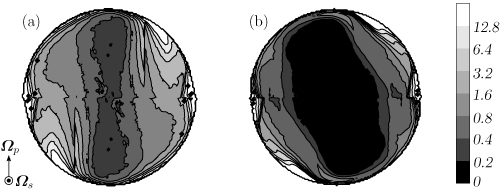
Fig.2 Temporally averaged enstrophy (squared vorticity) field of turbulence of (a) water and (b) the dilute surfactant (CTAC) solution. Re=4.0×10⁴，Po=0.1. The enstrophy indicates the existence of small-scale turbulent eddies. This figure quantitatively verifies the observation of Movie 2, i.e. the strong suppression of turbulent eddies by the surfactant additive.

 

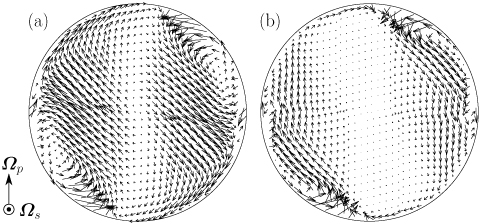
Fig.3 Temporally averaged velocity field of turbulence of (a) water and (b) the dilute surfactant (CTAC) solution. Re=4.0×10⁴，Po=0.1. Large vortical structures in the right-upper and bottom-left regions, which are clearly observed in the turbulence of water, still exist in the turbulence of the CTAC solution where small-scale eddies almost completely disappear.

 

References

[1]	Goto, S., Matsunaga, A., Fujiwara, M., Nishioka, M., Kida, S., Yamato, M., and Tsuda, S., Turbulence driven by precession in spherical and slightly elongated spheroidal cavities, Phys. Fluids, Vol. 26 (2014), 055107.
[2]	Goto, S., Shimizu, M. and Kawahara, G., Turbulent mixing in a precessing sphere, Phys. Fluids, Vol. 26 (2014), 115106.
[3]	Zakin, J. L., Lu, B. and Bewersdorff, H.-W., Surfactant drag reduction, Rev. Chem. Eng., Vol. 14 (1998), pp. 253-320.
[4]	White, C. M. and Mungal, M. G., Mechanics and prediction of turbulent drag reduction with polymer additives, Annu. Rev. Fluid Mech., Vol. 40 (2008), pp. 235-256.
[5]	Horimoto, Y. and Goto, S., Sustaining mechanism of small-scale turbulent eddies in a precessing sphere, Phys. Rev. Fluids, Vol. 2 (2017), 114603.