流れ 2005年9月号 目次
― レオロジー ~非ニュートン流体の流動~ ―
| リンク一覧にもどる | |
オプティカル・レオメトリーとその応用
 高橋 勉 長岡技術科学大学 |
1.はじめに
レオロジーは複雑流体の流れ挙動を表す構成方程式を明らかとし,連続体力学の手法によりそれらの流れ場が予測できるようにすることを目的としている.個別の流体に関してその流体を表す構成方程式中に定義された物質定数を実験により決定する方法をレオメトリーという.非圧縮性ニュートン流体が対象の場合,レオメトリーとは粘度測定に相当する.複雑流体の場合,構成方程式には複数の物質定数が存在し,それらすべてを実験的に明らかにするためには様々な条件における測定を行う必要がある.市販のレオメーターは定常粘弾性試験,動的粘弾性試験,過渡的粘弾性試験などが行えるようになっており,これらにより得られる情報を総合して様々な物質の流動特性を明らかにする.
レオメーターでは流動により発生する応力を流路壁面に作用する力より評価するため流れ場全体にわたる平均的な応力は測定できるが,流体内の分子配向やマクロ構造の変化などについては情報を得ることが難しい.たとえば棒状剛直分子が高密度で分散しているような液晶の場合,流動により液晶分子はタンブリング,ワギング,アライニングなどの運動状態をとることが知られている.しかし,レオメーターによる力学的な情報のみからこれらの運動状態を知ることは難しい.また,流動により分子構造が変化したりマクロ的な構造が形成したりするような物質も多々存在するが,ミクロ的な変化をレオメーターのみで明確にすることは困難である.複雑流体の正確な構成方程式を明らかにするためにも,流動によるミクロ的あるいはマクロ的な構造変化を測定することが必要となる.
2.オプティカル・レオメトリーとは
前置きが長くなってしまったが,流動によるミクロ的・マクロ的な物質構造の変化を光学特性や光学異方性の変化から計測しようとする技術をオプティカル・レオメトリーという.光学異方性を測定する技術には散乱や蛍光の計測,偏光解析などがある.散乱には計測が比較的易しい微小角散乱(Small angle light scattering: SALS)のほかにラマン散乱や中性子散乱などの高度の測定技術や大規模な装置が必要となるものもある.偏光解析では光学的に変調を加えたレーザー光などを用いて実時間で流動複屈折や二色性の変化を測定する技術が開発されている.いずれの手法においてもその結果のみで必要な情報が完全に得られるというわけではなく,複雑な現象を明らかにするためには他の光学的手法や力学的測定の結果をあわせて考察しなければならない.
3.光学異方性について
流体が光学異方性を発現する場合,その原因は固有効果と形状効果に大別される.固有効果とは流体を構成する分子構造に起因する光学異方性で,分子配向などのミクロ的な変化により発生する.形状効果は光の波長規模の構造の形成により発生するマクロ的な光学異方性である.それぞれの効果により発生する光学異方性には光の伝播速度の異方性に関係する複屈折性と光の吸収・散乱特性に関係する二色性の二つの性質がある.さらに,複屈折と二色性には直線偏光に対する異方性と円偏光に対する異方性が存在する.偏光解析や光散乱の測定ではこれらの効果が重ね合わせて検出されることが多く,いずれの効果が支配的であるかを知るためには各種の測定手法を組み合わせる必要がある.
4.オプティカル・レオメトリーによる測定例
次にオプティカル・レオメトリーの手法を使って行った研究の例をいくつか紹介する.いずれにおいても偏光解析により複屈折および二色性を測定しているが,時間的に変化する複屈折・二色性の実時間測定が著者の得意技であり,そのための計測系,フローセル,解析システムなどは様々な状況に対応できるよう多種のものを開発してある.
高分子流体は流動により顕著な粘弾性特性を示す.弾性力の効果によりニュートン流体では発生しない法線応力差が生じる.単純せん断流れにおいて流動方向を1,せん断方向を2とすると法線応力差は第1法線応力差N1(=σ11-σ22),第2法線応力差N2(=σ22-σ33)および第3法線応力差N3(=σ33-σ11)として定義される.定義からわかるように3つの法線応力差のうち2つが求まればその差より3つめも算出される.粘弾性特性により生じる多くの現象はN1の効果として説明可能である.さらに,円錐円板型流路を用いることにより市販のレオメーターでN1を測定することができるため弾性力の評価としてN1を用いることが多い.高分子流体の場合N2はN1に対して符号が逆で数分の1から10分の1程度の値を示すと言われている.曖昧な表現を使っているのはN2を正確に測定する方法が未だ確立していないからである.しかし,N2は単純せん断流れにおいては渦度軸方向(3方向)に作用する応力であり,流動不安定性に影響する可能性が高い.また,正確な構成方程式を導くためにも実験により厳密なN2を測定しておく必要がある.N2を測定する技術としてこれまでにも様々な手法が開発されている.しかし,著者の知るところ機械的手法を用いて定常流動時のN2を測定した結果は報告されているが,過渡的な流れ場におけるN2の時間変化を測定した結果はない.そこでオプティカル・レオメトリーの手法を用いてこの問題に挑んでみた.
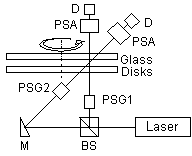
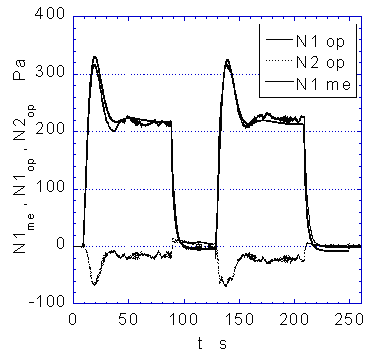
オプティカル・レオメトリーの重要な定理のひとつに光弾性則(Stress-Optic rule)がある.これは応力テンソルと屈折率テンソルが単純な比例関係にある,というものである.直鎖状高分子溶液ではずり速度の広範囲にわたってこの関係が成立する.比例定数は光弾性係数と呼ばれる物質定数であり,この値がわかっていれば屈折率テンソルを求めることにより応力テンソルの各成分を算出できる.屈折率テンソルの各成分は複屈折および配向角から算出できるが,全成分を測定するためには少なくとも異なる二方向からの複屈折測定を行う必要がある.そこで,同時に2方向から複屈折を測定できるDouble-Beam Rheo-Optical Analyzerを開発した.流路としては扱いが簡単な平行円板型を使用し,円板面に垂直方向と半径方向にある角度で傾けた傾斜方向より複屈折を測定する傾斜2光線測定法を確立した(1).その装置で使用している光学列の概略を図1に,実際の装置写真を図2に示す.測定された結果の例を図3に示す.図3においてはじめは流路を時計方向に所定の角速度で回転させ,一旦停止した後に反時計回りに同じ角速度で回転させている.せん断応力は回転方向により符号が逆転するがN1とN2は回転方向に依存しない.N2の測定手法が確立していないことからこの手法で測定されたN2の精度を検証することは難しいが,これまでに予測されている値とほぼ同値であった.
 |
|
||||||||||
| 図1 2光線式オプティカル・レオメーターの光学列 | |||||||||||

|
|
| 図3 ひも状ミセルを形成する界面活性剤水溶液(CTAB (cetyltrimethylammonium bromide)0.03 mol/l, NaSal (sodium salicylate) 0.23mol/l)のステップせん断流れ場におけるN1,N2の測定結果.(添え字opは光学測定による結果,meはレオメーターによる機械的測定結果を示す) |
4-2 流動誘起構造変化の測定(3)
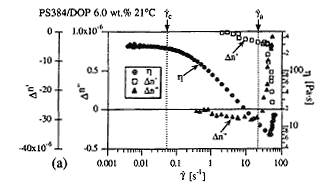
流動を加えることにより分子構造やマクロ的な構造が変化する現象として流動誘起構造変化や流動誘起相分離現象がある.構造の変化により流動特性が変化することが多いためレオメーターによる測定でも構造変化が起こることは計測できる.しかし,その構造がどのようなものであるかを予測することは容易ではない.著者は界面活性剤水溶液におけるミセル構造変化や液晶の相変化など流動に起因する構造変化現象についてこれまでに取り組んできている.図4で示す例は分子量約4百万のポリスチレンをDOP(Dioctyl Phtahalate)に6wt%で溶解させた溶液の流動誘起相変化現象における複屈折と二色性の測定結果を示している.応力制御型レオメーターにガラス製平行平板型流路を設置し,偏光変調を加えたレーザーを用いてせん断応力一定状態における複屈折と二色性をずり速度の時間変化と同時に測定した.レオメーターからの情報で,ずり速度が60s-1以上となるとずり粘ちょう化が発生し粘度が急激に大きくなることがわかる.これよりずり速度が60s-1以上の状態ではそれまでとは違う何らかの構造変化が生じることが予測される.しかし,この結果だけではそれ以上の詳細を推測することは難しい.流動複屈折はずり速度の増加に伴ってゼロから直線的に負の側に大きくなる.ここで測定される複屈折は分子構造に起因する固有複屈折の値であり,ずり流動による分子の配向を示している.複屈折は粘度と同じく60 s-1に達するまではり速度の増加により連続的に変化しており,ポリスチレンの分子は構造変化の発生まで流動配向し,特に異常を示さない.これよりこの範囲ではポリスチレン分子には大きな構造変化が生じていないことが推測できる.これに対応して,二色性はずり速度が20 s-1まではずり速度の増加に対して負の側に増加するが,20 s-1超えると正側に向けて増加に転じる.その時の増加こう配は極めて高い.微小角散乱において観察された特徴的なパターンとあわせて考察すると,二色性が負の小さな値を示す20 s-1以下の領域ですでに構造変化によるマクロ構造が発生しており,その構造はサブミクロン程度の大きさで流動方向に対して直角方向に細長い形状を持つことがわかった.さらに,60 s-1以上の領域ではこれらのマクロ構造が結合しバンド状の組織に変化することもわかった(図5参照).このように,いくつかの測定技法を複合し異なる光学異方性を比較することにより複雑な現象の本質を見いだす手がかりを得ることができる.
|
| |
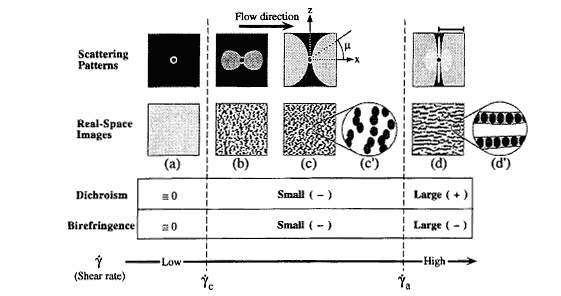 |
| 図5 光学測定により考察された構造変化の状態図 |
4-3 液晶分子のタンブリング挙動(4)
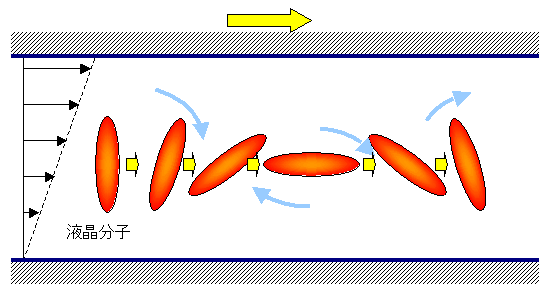
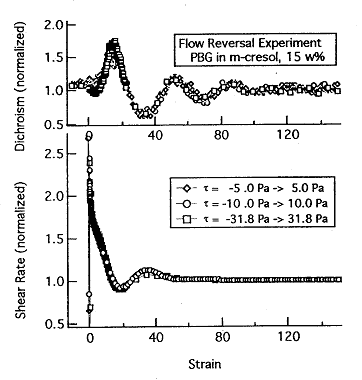
先にも述べたが液晶にずり変形を加えるとずり速度により液晶分子が様々な挙動を示す.ここでは二色性の変動からタンブリング挙動をとらえた例を示す.液晶としてPBG(Poly(benzyl glutamate))をm-cresolに15wt%の重量比で混ぜた溶液を使用し,平行平板型流路を用いてずり流動を加えた.タンブリングは図6に示すように液晶分子がせん断面(1-2平面)内で大きく旋回するように回転する状態である.個々の分子はそれぞれ異なる位相でタンブリングするため,定常流動状態で二色性を測定しても一定の値を示すだけである.しかし,長時間にわたり一定のずり速度で流動させた後に突然回転方向を逆転させそれまでと同じずり速度で流動を加えると,瞬間的に各分子のタンブリング位相が揃う.このときの二色性測定結果を図7に示す.逆回転直後から複屈折の規則的な変動が現れ次第に減衰していく様子が観察される.瞬間的に位相の揃ったタンブリングを行っている分子も時間経過とともに位相がずれてきて3~4周期程度の時間が経過すると元のランダムな位相状態に戻ることがわかる.この挙動は加えるせん断応力(この実験は応力制御型レオメーターを使用しているため応力一定条件で流動させている)を変化させても,ひずみを横軸として整理すると一本の線で挙動が表される.すなわち,タンブリングが試料の受けるひずみ量に依存することがわかる.
|
|
5.終わりに
現在は付加価値の高い新しい機能性流体が次々と開発されている.生理流体や食品系の流体などこれまで厳密な流動特性について研究がなされていなかった分野においても,流体力学的な取り扱いが必要になってきている.複雑流体の流動による状態の変化を知る必要性はますます広がるものと思われる.ふつうのマヨネーズとカロリー半分マヨネーズを光で見分けることができた.留学中に米国大手食品会社の研究員から受けた依頼がきっかけだった.必要は発明の母であり,何か計りたいものがあるという要望が新しい測定技術を考える原動力となる.オプティカル・レオメトリーの技術を通じて新しい素材や技術の開発,これまで不明であった現象の解明などの一翼を担えることを夢みている.さらなる新しい測定方法を検討するためにも『こんなものは計れるか?』といった質問・要望をお寄せいただけるとありがたい.(ただし,できなかったからと言って当方を責めないでくださる寛容なお心を切望いたします)
参考文献
- Takahashi T and Fuller GG, Stress Tensor Measurement Using Birefringence in Oblique Transmission, Rheol Acta, 35 (1996), 297-302.
- Takahashi T, Shirakashi M, Miyamoto K and Fuller GG, Development of a Double-Beam Rheo-Optical Analyzer for Full Tensor Measurement of Optical Anisotropy in Complex Fluid Flow, Rheol Acta, 41 (2002), 448-455.
- Kume T, Hashimoto T, Takahashi T and Fuller GG, Rheo-Optical Studies of Shear-Induced Structures in Semidilute Polystyrene Solutions, Macromolecules, Vol.30, No.23 (1997), 7232-7236.
- Takahashi T, Vermant J, Fuller GG and Mewis J, Simultaneous Mechanical and Optical Measurement of a Polymer Liquid-Crystal in Transient Shear, Proc. The Pacific Conference on Rheology and Polymer Processing (1994), Kyoto, 29.

