流れ　2008年4月号　目次

―　特集： 次世代二相流研究　― まだ道なかば　－船の抵抗とマイクロバブル－ 加藤 洋治（東洋大学） 気泡流だけに見られる面白いウエイク構造 村井 祐一（北海道大学） サブミリスケールの気泡発生制御とその計測 真田 俊之（静岡大学） 自由エネルギー拡散界面モデルの二相流数値解析への導入 高田 尚樹（産業技術総合研究所） マイクロチャネル積層型熱交換器における熱交換特性と微細管内の気液二相流動現象 藤原 暁子（筑波大学） オランダ　トゥウェンテ大学滞在記 杉山 和靖（東京大学） バブルリングの形成過程の観察（流れの夢コンテストに参加して） 杉本 康弘（金沢工業大学） 編集後記（牛島，深潟，北川） 　｜　リンク一覧にもどる　｜

 

自由エネルギー拡散界面モデルの二相流数値解析への導入

高田 尚樹 独立行政法人 産業技術総合研究所

１．はじめに

　様々な分野で見られる気液・液液二相流の数値解析研究で，Level-Set（LS）法，Front-Tracking法，Volume of Fluid（VOF）法等は，界面を直接捕捉・追跡することでその現象を詳細に解明できる有効な計算法として計算機の性能向上とともに普及してきた．最近では，VOF法の一種のMARS法⁽¹⁾に，LS法と高精度の移流計算が可能なCIP法⁽²⁾を協調させて体積保存と界面形状捕捉の両方に優れる計算法⁽³⁾や，VOF法と多流体モデルに基づく平均化法の融合により大/小スケールの界面を同時に扱うことができる方法^(4),(5)等が開発され，実機設計支援のための二相流解析で利用されている．

　 界面を通した熱･物質輸送が起こる相変化や溶解を伴う二相流や，濡れ性が不均一な固体表面上を界面が移動する接触線問題の解析に対して，上記の計算法では，高度な幾何学演算を駆使する界面の移流・形状構成アルゴリズムは複雑になりやすい．このような界面が流体と異なる移動速度を持ち得る二相流の解析の困難さは，界面を連続体の立場から厚さのない移動境界と単純化したことに起因する．界面厚さは一般にナノメートルオーダーだからマクロスケールでそう考えることは間違いではないが，そのような界面モデルを採用する二相流解析では気泡核形成のような微視的現象も考慮する場合に界面近傍のより小さなスケールの物理的な情報の補完が求められる．

 

２．自由エネルギー理論に基づく拡散界面モデル（DIM）

上記の二相流数値解析の課題を克服するため，従来と異なるアプローチとして，非平衡系の自由エネルギーの考え方^(6),(7)に基づく拡散界面モデル（Diffuse-Interface Model，DIM）を導入する計算法が近年国内外の研究者によって提案され，様々な問題へ適用されつつある⁽⁸⁾．

　 DIMでは，平衡状態に向けて多相・多成分系の自由エネルギーを最小化するように，化学ポテンシャルの局所勾配で生じる拡散流束によって物質が移動して各相の析出や分離が自律的に起こる．二相系の自由エネルギーは一般に，密度や濃度などを変数とする二重井戸ポテンシャルとそれらスカラー量の局所勾配の二乗に比例する増分を用いて定義される．界面は，後者の寄与によりある相から別の相へ物性が連続的に変化する有限領域として現れ，上述の拡散流束によって一定幅に維持される．また，表面張力は，界面領域内の局所勾配起因の単位面積当たりのエネルギー増加の積分として定義される．以上の結果，DIMの系の時間発展は，界面に対して瞬時局所の形状や移動速度の拘束条件を陽に課すことなく，界面を含む全領域に渡って同じ偏微分方程式で統一的に記述される．

　 DIMアプローチは，元々は材料科学分野で始まり，そこでは一般にPhase-field法（PFM）^(9),(10)と呼ばれる．PFMは，相変態に伴う微視的組織形成過程の解明と材料設計に有効な手段として合金や高分子薄膜⁽¹¹⁾のメゾスケール解析で既に積極的に活用されている．

 

３．DIMを用いた二相流計算法

　上述のようなメゾスケールの連続体としての界面の特徴を利用して，二相流のDIM計算法では，図1に示すように，マクロな連続体としての流体相の挙動を記述するNavier-Stokes（NS）方程式が界面内部でも同様に成り立つと仮定する．そして，界面を含む領域全体を有限幅の計算セルで離散化して各物理量の空間微分を有限差分近似で評価することにより，従来の各種計算スキームと解法アルゴリズムを適用して全領域でその支配方程式を解く．以上により，自由エネルギーというキーワードを通して流体力学と非平衡熱力学の両方に立脚するDIM法は，複雑な幾何学演算なしでも界面の形状と移動を自然に流れ場に反映するため，相変化や溶解，接触線問題を含め二相流全般の解析が容易になるとともに，複雑な現象をより小さなスケールから捕らえることで高精度に予測する可能性を持っている⁽⁸⁾．

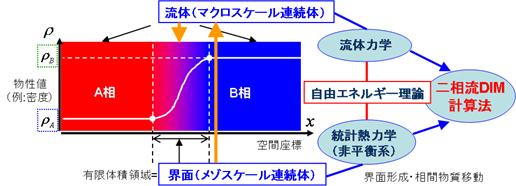
図1. 拡散界面モデルに基づく二相流計算法の概要

　二相流DIM法には，NS式を直接解くもの ^(12),(13)と，仮想的な流体粒子の離散速度分布関数の時間発展式を解く格子ボルツマン法⁽¹⁴⁾がある．これらは当初，主に密度比の小さい問題に適用されてきたが，近年は計算スキームやアルゴリズムの改良によって水-空気系のような大きな密度差の二相流を扱うことができるようになっている^(15)-(18)．これまで日本の二相流解析分野では，国外と異なり，従来計算法に比べてDIM法は殆ど注目されていなかった．しかし最近では，多くの研究者によって様々なDIM法の提案と問題への適用が進みつつある．

　 マクロスケールの連続体近似に基づく流体力学方程式を界面領域でも扱うことから，二相流DIM法では通常，界面領域の幅は計算セル1個の幅よりも厚く，実在する界面のものよりもはるかに大きくなり，従来法^(1),(3)-(5)と比べても大きい．このような界面のスケールの点で，現在多くの二相流DIM法は，解析領域全体がナノ・マイクロスケールにある材料分野のPFMとは異なり，大胆な連続体仮定に支えられているといえる．その一方で，本計算法は，様々な二相流の実験，理論，他の計算法による結果と比較して妥当な結果を与えており，このマルチフィジックスな界面のメゾスケール連続体モデルはマクロスケール解析にも有効であることが示されている^{(8),(15)-(18)}．

 

４．二相流解析結果

　ここで，筆者らが行ったDIM法による二相流解析例を紹介する．計算領域は，デカルト座標系で一定幅の正方および立方セルの構造格子により一様に離散化されている．また，図中では，有限厚さを持つ界面は，気液両密度の中間値の等高面で代表されている．

4･1　液柱の崩壊⁽¹⁹⁾
　高密度比二相流DIM法⁽¹⁸⁾の検証のため，重力下における2次元閉空間内の液柱崩壊の解析を行った⁽¹⁹⁾．ここでは，空気-水系を想定し，液柱の初期アスペクト比2，幅αを10セルと18セルとした場合の結果を示す．図2のように，界面厚さは，各無次元時刻t*（空気-水系で0.1，0.2，0.3秒）で数値的な振動や過剰な拡散なしに一定に保持されている．本結果は他の計算や実験の結果と良く一致する⁽¹⁹⁾．

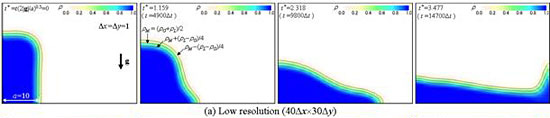
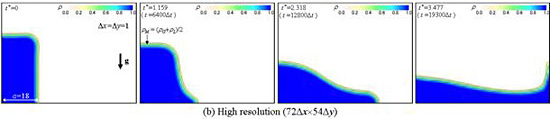
図2 重力下における2次元液柱の崩壊
（a: 初期の液柱幅，気液密度比ρ_L/ρ_G=802，動画1: (a) a = 10，動画2: (b) a = 18）

 

4･2　液滴の落下
　ここでの解析では，すべり壁で囲まれた空間内の重力下の空気中に直径10 mmの球形水滴を高さ73 mmに初期配置し，その下方に深さ30 mmの貯水域を想定した．この空間を48×48×250個の立方形セルで離散化し，液滴径を30セル幅に設定した．図3に示す各無次元時刻t*の界面形状の結果は改良型VOF法による結果⁽²⁰⁾と定性的に一致する．界面近傍の空間解像度を上げれば，DIM法の結果は他の計算法の結果と一層良く一致すると考えられる．

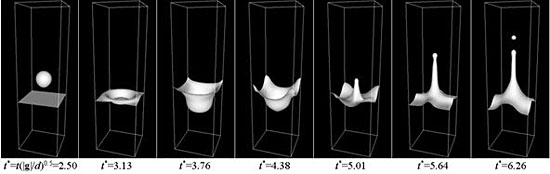
図3 自由落下液滴

4･3　濡れが不均一な固体表面上の液滴の挙動⁽²¹⁾
　次に，濡れ性が不均一な固体面上の液滴挙動解析⁽²¹⁾を述べる．対象は，無重力下の空気中の直径16 mmの水滴である．図4に示す条件(a)に対して，液滴は，毛管力の違いによって撥水面（接触角θ_W1 = 119°）から親水面（θ_W2 = 61°）へ移動した（図5）．一方，条件(b)では，液滴は左右の親水面に引っ張られて中央の撥水面を境に2つに分裂した（図6）．これらの検証は今後の課題であるが，重力下の数値解析を通して接触角と毛管力が精度良く評価されていることを確認しており，本DIM法の濡れ性境界条件^(22),(23)と表面張力は適切なものと考えられる．

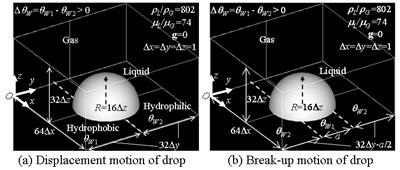
図4 固体表面上の液滴挙動の解析条件（接触角θ_W1=119°, θ_W2=61°）

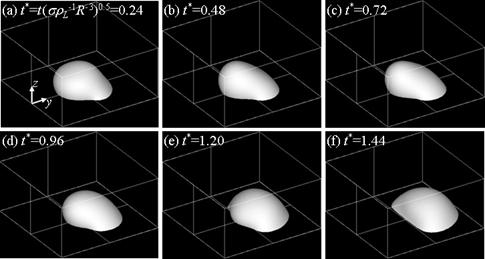
図5 条件(a)における液滴のスライド運動（動画）

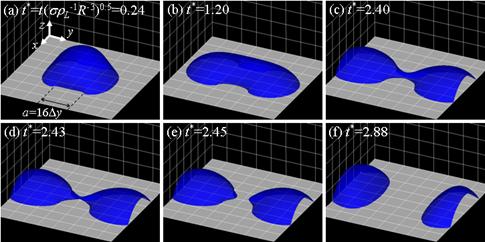
図6 条件(b)における液滴の分裂（動画）

4･4　物体周りの相変化を伴う流れ^(23),(24)
　最後に，ファンデルワールス状態方程式とNS式を用いた，幅20×高さ5セルの2次元等温物体周りの非理想流体流れの解析^(23),(24)を述べる．計算では，密度比約1.53の二相が共存しうる臨界点付近の飽和圧力p_Sの液相で満たした領域を300×50セルで離散化し，上下にすべり境界，左側に流速Uinの一様流入境界，右側に一定圧p_outの自由流出境界を置いた．本解析での，キャビテーション数Cav = (P_out-P_S)/(ρ_LUin²/2)の増加に伴う物体周囲の気相発生の減少傾向（図7）は実際の現象と定性的に一致する．以上はDIM法による相変化二相流の試験的解析例であり，基礎的適用性は実証されたと思われるが，詳細な評価とより現実に近い問題への適用は今後の課題である．また，今回の方法以外にも相変化を扱うDIM法が幾つか提案されている^{(13),(25)-(27)}．

　
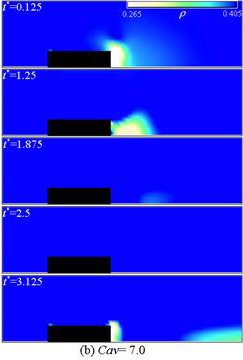
図7 物体周りの2次元ファンデルワールス流体流れ
（Reynolds数2.03，キャビテーション数Cav = 0, Cav = 7.0，動画: (a), (b)）

 

５．おわりに

　本報では，気液・液液二相流解析のための拡散界面モデル（DIM）に基づく計算法^{(8),(12)-(19),(21)-(27)}を紹介した．４．の解析ではシンプルなDIM法^(18),(23)を用いているが，他にも様々なより高度なDIM法が提案されてその能力が証明されるとともに，従来法の表面張力評価へのDIMの部分的応用^(20),(28)や，実際のナノ・マイクロデバイスの混相流問題等への適用も最近数多く行われている^(29)-(31)．しかし，二相流DIM法の歴史は他の計算法と比べて浅く，界面の厚さや形成，表面張力などに関して様々な課題があり，本格的な相変化二相流問題への適用もこれからである．今後，DIMの重要性が多くの研究者に認識され，DIM法が既存の様々な計算技法を取り込んで高精度化し，さらに従来法^(1)-(5)と融合してより高度な二相流計算法が開発されることが期待される．また，現在の二相流解析だけではなく，より小さなメゾスケールにおける気相・液相・固相の違いに依存しないシームレスな連続体の統一的数値解析や，マルチスケールシミュレーション⁽³²⁾において固気液相変化を伴う流体－構造連成問題の取り扱いにDIMが寄与することも考えられ，そのための分野横断的な議論も行われている⁽³³⁾．

 

謝　辞

　本稿執筆では，日本機械学会創立110周年記念2007年度年次大会の先端技術フォーラム「連続体力学に基づいた相変化・相変態・相転移の数値シミュレーションにおける新展開」（No.F01, 計算力学部門企画）における，広島大学･岩本剛先生との共同で企画したフォーラム趣旨，ならびに講師の皆様の講演内容⁽³³⁾も参考とさせていただきました．ここに御礼申し上げます．

参考文献

(1)	Kunugi, T., Transactions of the Japan Society of Mechanical Engineers, Series B, Vol. 63, No. 609 (1997), pp. 1567-1584.
(2)	Yabe, T. and Wang, P. Y., J. Phys. Soc. Japan, Vol. 60 (1991), pp. 2105-2108.
(3)	Himeno, T., Nonaka, S., Naruo, Y., Inatani, Y., and Watanabe, T., JSME Int. J. Ser. B-Fluids Therm. Eng., Vol. 47, No. 4 (2004), pp. 709-715 (http://www.jstage.jst.go.jp/browse/jsmeb).
(4)	Shimada, N., Tomiyama, A., Maekawa, M., Suzuta, T., and Ozaki, T., Kagaku Kogaku Ronbunshu, Vol. 31, No. 6 (2005), pp. 377-387.
(5)	Masuda, R. and Nagaoka, M., Proceedings of the 20th Computational Fluid Dynamics Conference (2006-12), CD-ROM, Paper No. A6-1.
(6)	van der Waals, J. E., Transl. Rowlinson, J. S., J. Stat. Phys., Vol. 20 (1979), pp. 197-244.
(7)	Cahn, J. W. and Hilliard, J. E., J. Chem. Phys., Vol. 28 (1958), pp. 258-267.
(8)	Anderson, D. M., McFadden, G. B. and Wheeler, A. A., Annu. Rev. Fluid Mech., Vol.30 (1998), pp. 139-165.
(9)	Koyama, T. and Onodera, H., J. Phase Equilib. Diff., Vol. 27(2006), pp. 22-29.
(10)	Uehara, T. and Tsujino, T., Transactions of the Japan Society of Mechanical Engineers, Series A, Vol.72 (2006), No. 716, pp. 438-444.
(11)	Morita, H., Kawakatsu, T. and Doi, M., Macromolecules, Vol. 34 (2001), pp. 8777-8783.
(12)	Jacqmin, D., J. Comput. Phys., Vol. 155 (1999), pp. 96-127.
(13)	Jamet, D., Lebaique, O., Coutris, N. and Delhaye, J.M., J. Comput. Phys., Vol. 169 (2001), pp. 624-651.
(14)	Chen, S. and Doolen, G. D., Annu. Rev. Fluid Mech., Vol.30 (1998), pp. 329-364.
(15)	Teng, S., Chen, Y. and Ohashi, H., Int. J. Heat Fluid Flow, Vol. 21 (2000), pp. 112-121.
(16)	Inamuro, T., Ogata, T., Tajima, S. and Konishi, N., J. Comput. Phys., Vol. 198 (2004), pp. 628-644.
(17)	Kim, J., J. Comput. Phys., Vol. 204 (2005), pp. 784-804.
(18)	Takada, N. and Tomiyama, A., JSME Int. J. Ser. B-Fluids Therm. Eng., Vol. 49, No. 3 (2006), pp. 636-644 (http://www.jstage.jst.go.jp/browse/jsmeb).
(19)	Takada, N. and Tomiyama, A., Theoretical and Applied Mechanics Japan., Vol. 55 (2006), pp. 148-156 (http://www.jstage.jst.go.jp/browse/nctam).
(20)	Hayashi, K., Doctoral Thesis (2007), pp. 90-92, Kobe University, Japan.
(21)	Takada, N., Matsumoto, J., Matsumoto, S. and Ichikawa, N., Proceedings of the 6th International Conference on Multiphase Flow (2007-7), CD-ROM, Paper No. S1_Thu_D_61.
(22)	Yoshino, M. and Mizutani, Y., Math. Comput. Simulat., Vol. 72 (2006), pp. 264- 269.
(23)	Takada, N. and Tomiyama, A., Int. J. Mod. Phys. C, Vol. 18, No. 4 (2007), pp. 536- 545.
(24)	Takada, N. and Tomiyama, A., Progress in Multiphase Flow Research, Vol. 2 (2007), pp. 173-180 (http://www.jstage.jst.go.jp/browse/pmfr/).
(25)	Jamet, D. and Ruyer, P., Proceedings of the 5th International Conference on Multiphase Flow (2004-5), CD-ROM, Paper No.169.
(26)	Seta, T. and Okui, K., Journal of Thermal Science and Technology, Vol. 1, No. 2 (2006), pp. 125-137 (http://www.jstage.jst.go.jp/browse/jtst).
(27)	Tsujimoto, K., Mizutani, Y., Shakouchi, T. and Ando, T., Proceedings of the 19th Computational Mechanics Conference, No.06-9 (2006-11), pp. 273-274.
(28)	Hayashi, K., Takada, N. and Tomiyama, A., Japanese Journal of Multiphase Flow, Vol. 20, No.3 (2006), pp. 244-251 (http://www.jstage.jst.go.jp/browse/jjmf).
(29)	Inamuro, T. and Ii, T., Math. Comput. Simulat., Vol. 72 (2006), pp. 141- 146.
(30)	He, Q., Fukagata, K. and Kasagi, N., Proceedings of the 6th International Conference on Multiphase Flow (2007-7), CD-ROM, Paper No.S7_Wed_C_40.
(31)	Inoue, G., Yoshimoto, T., Matsukuma, Y. and Minemoto, M., J. Power Sources, Vol. 175 (2008), pp. 145-158.
(32)	Hasebe, T. et al., Journal of the Japan Society of Mechanical Engineers, Vol.108, No.1043 (2005), pp.763-817.
(33)	Proceeding of Mechanical Engineering Congress, 2007 Japan (MECJ-07), No.07-1 (2007-09), pp.147-158.