流れ 2010年12月号 目次
― 特集テーマ: 空力騒音 ―
| リンク一覧にもどる | |
「光」と「CT」を用いた超音速ジェット騒音の断層可視化手法
荒木幹也 群馬大学
|
1.はじめに
本研究では,「音」の計測に「光」を用いる.流体騒音の音源は「流れの中」にあり,従来のマイクロフォンを用いた計測には制限が付きまとう.光を用いることで,これまで困難であった流れの中での音響計測を可能とする「光学CT法」を提案する.一種のシュリーレン光学系とCT(Computed tomography)を組み合わせることで,超音速ジェット内部から周囲雰囲気にわたる幅広い領域における音響計測が可能となる.また様々な周波数成分の重畳騒音であっても,それぞれの周波数成分ごとの解析が可能となる.本稿では,光学CT法(1)の概略と,軸対称不足膨張ジェットを対象として行った計測事例について紹介する.
次世代超音速輸送機開発において,エンジン排気騒音低減は大きな課題の1つである.超音速飛行用ジェットエンジン排気は不足膨張ジェットであり,スクリーチ(2)が放出される.スクリーチは,衝撃波(ショックセル)と渦との干渉が,フィードバックループを形成することで生じる.非常に狭い周波数域に大きなエネルギーが集中するため,騒音問題のみならず機体の破損にもつながり大きな問題となっている.その発生メカニズム解明や騒音低減デバイス開発など,スクリーチに関連して多くの研究が行われてきた(2 -12).騒音低減デバイス開発において重要なのは,音源の位置と規模の把握である.患部(音源)の詳細診断(可視化)が,治療(騒音低減)の成否を握ると考えている.
2.計測対象ならびに光学系
図1に,計測対象である不足膨張ジェットの連続シュリーレン像を示す.出口直径8.0 mmの円形先細ノズルを用いた.ノズル出口中心を原点とし,流れ方向にz軸,半径方向にr軸をとる.圧力比2.25(ジェットマッハ数1.14)の不足膨張ジェットを噴出する.作動流体は常温の空気である.ノズル出口から噴出後,周囲大気との圧力不整合からショックセルが形成される.ショックセルの振動モードはトロイダル(軸対称)であり,音響放射のパターンも軸対称に近いと仮定して計測を行った.
図2に,光学CT法概略を示す.CWレーザを用いた一種のシュリーレン光学系である.音は圧力変動であり,圧力と同時に密度も変動する.この密度変動をシュリーレン光学系で検出する.実際の光学系は,配置の都合上ミラーを用いて光路が折りたたまれている.ここでは簡単のため,光路を直線上に展開した状態で説明する.
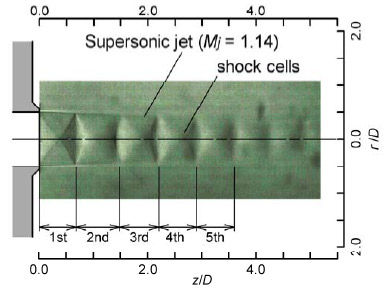
Fig.1 Time averaged schlieren image of under-expanded jet.
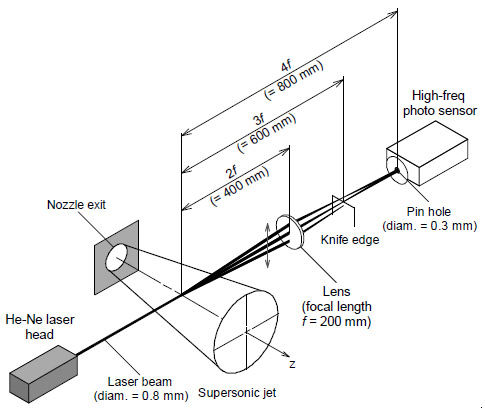
Fig.2 Schematic of optical CT method.
光源にHe-Neレーザ(λ = 632.8 nm)を用いた.レーザビームは,ジェット内部ならびにその周囲を透過する.レーザビームは凸レンズによって集光され,焦点を結ぶ.光路上の密度勾配に応じてレーザビームは屈折し,焦点の位置は移動する.ここにナイフエッジを設置しその一部をカットすることで,レーザビーム屈折角の変化を輝度変化に変換する.レンズの焦点距離fを変更することで,光学系の感度を変更することが可能である(13).本研究では,密度変動の大きいジェット内部も含めた計測を行うため,感度を低めに設定した.本研究では,ナイフエッジを流れと平行に設置した.ナイフエッジの向きを変更することで,取得する密度勾配の方向つまり音波の伝播方向を任意に選択することができる.
ナイフエッジ通過後の位置にスクリーンを設置し,計測部のシュリーレン像を投影する.スクリーンには直径0.3 mmのピンホールが設置されており,計測領域を限定する.ピンホール直径は,空間分解能に対応する.ピンホールを通過したレーザビームは,高速フォトセンサに入射し,輝度変化が検出される.高速フォトセンサからの輝度信号は,デジタルオシロスコープでA/D変換され記録される.サンプリングクロックは,2.0 μsである.取得されたデータは高速フーリエ変換され,輝度変動の周波数分布が求められる.取得された周波数分布から,断層可視化を行う周波数成分の輝度振幅を抽出し記録する.それぞれの周波数成分について,独立に解析が可能である.以上の手続きを,ジェット半径方向に0.5 mm間隔,流れ方向に1.25 mm間隔でスキャンしながら行う.
3.アーベル変換
フォトセンサで得られる輝度信号はレーザビーム光路上で起こった全ての事象の積分値であり,どの位置でどれだけ光路が屈折したのか分からない.そこで,CTスキャンなど医療分野で多用されるアーベル変換を行う.CTスキャンでは,人体を透過したX線の減衰量から人体組織の内部構造を断層可視化する.光学CT法では,音響場を透過したレーザビームの屈折量から密度変動分布の内部構造を断層可視化する.シュリーレン法では,密度勾配のうち光軸に対して垂直方向の成分のみが屈折に作用するため,ベクトル成分を考慮した独自のアーベル変換を行う.アーベル変換の詳細については参考文献(14)を参照されたい.
図3に,密度勾配によるレーザビーム屈折の概略を示す.簡単のため,軸対称場を対象とする.ジェット中心を原点とし,レーザビームの進行方向にY軸,レーザビームの進行方向と垂直方向にX軸をおく.原点からの距離をrとおく.流れ場は軸対称であるものの,レーザビームは直進する.ここでは参考文献(14)にならい,流れ場については円筒座標系(r,z,θを小文字で標記)を,レーザビーム透過位置については直交座標系(X,Yを大文字で標記)を用いる.
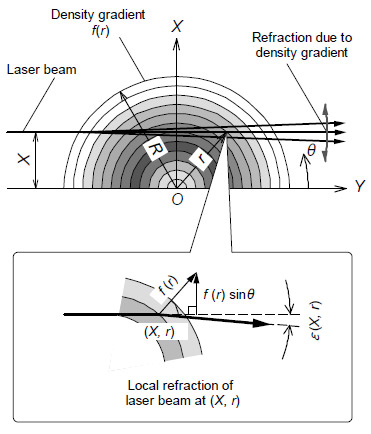
Fig. 3 Schematic of laser beam refraction due to density gradient.
ある半径位置rにおける局所密度勾配を,
| |
(1) |
とおく.局所的なレーザビーム屈折角は,局所密度勾配f ( r ) に比例する(14).ある座標( X, r )におけるレーザビーム屈折角ε ( X, r ) は,
| |
(2) |
と表される.ただし,c1は定数である.レーザビーム屈折角ε ( X, r ) は密度勾配のX軸方向成分のみに影響を受けるため, ( = X / r )を乗ずる必要がある.このようなベクトル成分を考慮する手続きは,通常のアーベル変換には含まれない.本研究では,以下の式(7)の変数変換を行うことで,この問題を通常のアーベル変換に帰着する.式(2)を,レーザビーム光路に沿って(Y軸に沿って),X < r < Rの範囲で積分した値が,光路長全体にわたるレーザビーム変位Ε ( X )となる.
|
(3) |
あるレーザビーム位置Xにおいてフォトセンサで検出される輝度変化J ( X ) を,次式のように置く.
| |
(4) |
ただし,I0はレーザビームの屈折が無い場合の輝度,ΔI ( X ) はレーザビーム屈折による輝度変化分である.このときJ ( X ) は,光路長全体にわたるレーザビーム変位Ε ( X ) に比例する(14).
| |
(5) |
式(5)を用いて式(3)を書き直すと,
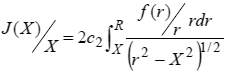 |
(6) |
が成立する.ただし,c2は定数である.ここで,
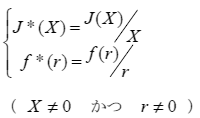 |
(7) |
の変数変換を行うことで,式(6)は次式に帰着される.
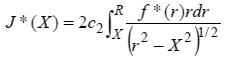 |
(8) |
式(8)は,核の位数1/2のアーベル積分方程式であり,解析的に次式のように解くことができる(14).
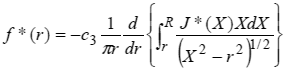 |
(9) |
ただし,c3は定数である.式(9)により,フォトセンサで検出される輝度変化J* ( X ) から,局所密度勾配f* ( r ) を再構成することができる.実際の計測では,その点数に限りがあるためJ* ( X ) は離散的数列となる.本研究では,Barrの方法(14)を用い,式(9)を線形行列式に帰着する.式(9)を用いることで,透過信号である輝度変動から,ジェット内部ならびに周囲にわたって広がる音響場における密度変動分布を断層可視化する.
4.断層像再構成
図4に,フォトセンサで検出される輝度変化のスペクトルを示す.縦軸は輝度振幅A J,横軸は周波数f,奥行き方向にはレーザビーム位置X/Dを示す.約28 kHzに,スクリーチによるスパイク状のピークが観察される.ピークは,ジェット外縁(X/D = 0.5)近傍で最大となり,周囲大気へ伝播するに従い減衰していく.ただし図4は,音響場を直線的に透過するレーザビームの輝度変動から得られたものであり,本来軸対称であるはずの現実の音響場の現象をそのまま表しているわけではないことに注意されたい.
今回の可視化事例では,スクリーチ音源の断層可視化を試みる.対象となるスクリーチ周波数成分(28 kHz)のみを抽出する周波数分離を行い,フォトセンサで計測される輝度振幅AJ, n(X) から,局所的な密度勾配振幅Af, n(r) を求める.ここでnは,n番目の周波数成分であることを示す.
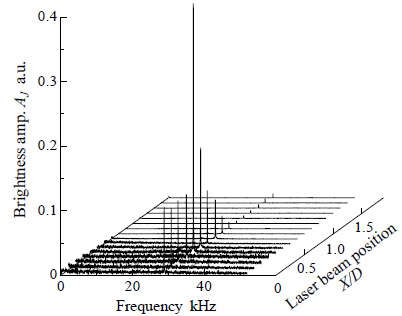
Fig. 4 Jet noise spectra obtained with photo sensor at z/D = 2.5.
図5に,アーベル変換によって再構成された密度勾配振幅の断層像ならびに連続シュリーレン像を示す.図5の上半分は再構成された密度勾配振幅Afの等高線,下半分は連続シュリーレン像を示す.密度勾配振幅Af はその最大値で無次元化されている.図5中の黒点は,レーザビーム透過位置を示す.流れは左から右向きである.図5より,超音速ジェットと周囲大気とのせん断層で,密度勾配振幅が極大値をとる領域が離散的に観察される.また超音速ジェット中心軸近傍でも,密度勾配振幅が極大値をとる領域が離散的に観察される.密度勾配振幅が大きな領域とショックセル構造とは一致しており,渦の通過によりショックセルが周期的に変形する移動衝撃波(12)が形成されていると考えられる.密度勾配振幅は第4ショックセル近傍で最大値をとり,スクリーチ音源がこの付近に存在すると考えられる.
図6に,アーベル変換によって再構成された密度勾配振幅断層像ならびに瞬間ミー散乱像を示す.図6の上半分は再構成された密度勾配振幅Afの等高線,下半分は瞬間ミー散乱像を示す.ミー散乱像から求めたジェット外縁を点線で示す.図6より,z/D = 2 ~ 3付近から,周期的な渦(図中矢印)が発達し始めることが分かる.この位置は,第3 ~ 第4ショックセルに対応する.周期的な渦は,ショックセルを変形させ音波を放出する.音波の一部はノズル出口に到達し,じょう乱源となり次の渦形成のきっかけとなる.このフィードバックループがスクリーチの原因となる(2,12).ショックセルを変形させるのに十分なまでに渦が発達し,スクリーチの音源となることが分かる.
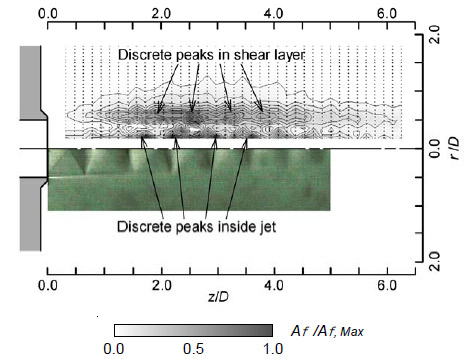
Fig. 5 Re-constructed density gradient amplitude at screech frequency
and time-average schlieren image.
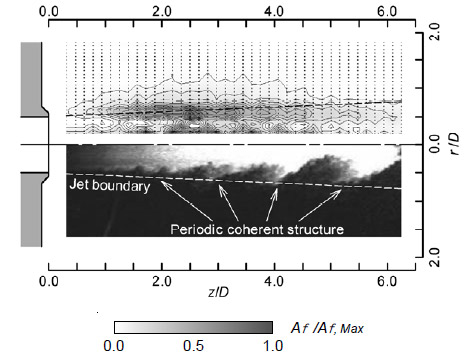
Fig. 6 Re-constructed density gradient amplitude at screech frequency
and instantaneous Mie scattering image.
5.まとめ
「光」と「CT」を用いた「光学CT法」を開発し,これまで直接計測することが困難であった流体騒音源の断層可視化を試みた.軸対称不足膨張ジェットの断層可視化では,ジェットと周囲大気とのせん断層ならびにジェット中心軸近傍に,密度勾配変動の極大値が離散的に観察される.ショックセルと密度勾配変動の構造は密接な関係を持っており,音源として振舞っていることが示唆された.多くの課題が残されているものの,計測法としての実現可能性が示唆されたと考えている.今後この技術を,様々な流体騒音へ適用していきたいと考えている.
文 献