流れ 2010年12月号 目次
― 特集テーマ： 空力騒音 ―
｜ リンク一覧にもどる ｜ |
空力音響解析のすゝめ
飯田明由
|
１．マジックパイプからの音
皆さんはマジックパイプという玩具をご存知ですか？図1に示すような直径25ｍｍ程度，長さ80cm程度の蛇腹のついたパイプです．この玩具の一端を持ち，図2のように振り回すと強いピーク性の音が発生します．古くは九州大学の中村先生ら(１)の研究報告もありますが，私は坂尾富士彦先生から教えていただきました．もの自体は非常に簡単な構造ですし，強いピーク性の音がでるのは，蛇腹部にあるキャビティ部で流れ場と音場が共鳴するためと予想できますが，まじめに実験や計算してみようとすると案外難しいようです．学会発表などで坂尾先生が再現性のある実験を行うことも難しいし，音の周波数を予測するのもそれほど簡単ではないですと話されていたことを思い出します．
実際にマジックパイプを振り回してみると，615Hz，90dBの音が発生しました．振り回したときの回転数は1秒間に1回から2回程度でしょうか．このとき，パイプの端部の周速度は約10m/s程度になります．パイプの中を流れている気流の平均速度は正確にはわかりませんが，周速度が10m/s程度ですから，速くても数m/s，実際にはパイプの入り口で風が流れているようには感じませんので，たかだか1m/s程度ではないかと思われます．そこで，パイプの内部の流速を1m/sと仮定して，キャビティ音の研究で有名なRossiter(2)の式
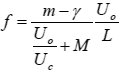
を使って，音の周波数を推定してみます．ここで，U0は主流速度，Ucは渦の移動速度，Lはキャビティの長さ，mは音響モード数でキャビティ間にある渦の個数に相当します．また，gは渦がキャビティ後端部を通過してから音が発生するまでの位相遅れ定数を表します．Lは計測すればわかりますが，ほかの値は正確にはわかりませんが，仮にUo=1m/s, Uc/ U0=0.5, g=0.25，モードを2として計算してみると音の周波数は535Hzと予測されます．まあ，あっていると言えばあっているし，あっていないと言えばあっていません．そもそも本当にこの現象が一般的なキャビティ音の理論が適用できるのかどうかもあまりはっきりしません．主流速度が正確にわからないので，あまり正確なことはわかりませんが，主流速度を1m/s程度と仮定すると動圧が0.6Paですから，圧力変動はその1/10程度と見積もれます．一方，発生した音のレベルは正確に測定できていて90dBでしたから，音の圧力は0.6Paと考えられます．すなわち，流れ場の圧力変動よりも音の圧力変動のほうが大きい，あるいは同程度のオーダーということになります．
さて，この問題を我々はコンピューターで解析できるでしょうか？
 |
 |
| 図1 マジックパイプ | 図2 マジックパイプで遊んでいる様子 |
2. 空力音響解析の現状と課題
ここでひとまずマジックパイプの問題は後回しにして，空力音響解析の現状と課題について考えてみましょう．空力音として一番身近な例は冬の寒い日に，木枯らしが吹いて，電線や木の枝から聞こえてくる風切り音ではないでしょうか．風切り音といえば誰でもヒューヒューという音をイメージすると思いますが，同じ音を繰り返して擬音を構成していることから，この音が周期的な音であると多くの人が感じているのだと思います．この音は，ギリシャ神話の風の神AeolusにちなんでAeolian toneと呼ばれることもあります．この現象は当初は，風によって物体が振動することによって音が発生すると考えられていましたが，1952年のLighthillの研究(3)(4)によって，物体の振動そのものによる音ではなく，流れ場の運動によって音が生じることが理論的に明らかになりました．その後，Curle(5)による物体表面の圧力変動に起因する音の発生メカニズムやPowell(6)，Howe(7)による渦音の理論が発表され，風きり音が渦の非定常運動に起因することが明らかとなりました．これらの先駆的な研究から50年近くが過ぎ，今日の計算機の進歩により，流れと音の解析が行えるようになりつつあります．その様子を紹介しましょう．
ところで，空力音の計算は何故そんなにも難しい（と言われる）のでしょうか，理由はいくつかありますが，そのひとつとしてLighthillが導いたLighthill方程式が連続の式，NS方程式，音速の定義式だけを使って導くことができることにあると考えられます．大学院の演習課題にするような式の変形だけでLighthill方程式が得られるということは（途中に特別な仮定やモデルはない），Lighthill方程式はNS方程式を波動方程式の形式に書き換えただけという風にも言えます．
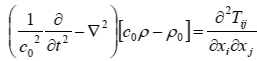
ここで
はLighthillテンソルと呼ばれるテンソルであり，波動方程式の音源項に相当します．このため，Lighthill方程式はNS方程式と同じ程度の難しさを有しています．言い換えれば，波動方程式の右辺に流体運動の非線形性に起因する難しさを凝縮したような形式となっています．Lighthillテンソルを渦度と速度の外積の発散項に置き換えたのがPowellの理論ですが，いずれにしても音源項が流体運動に起因する非線形項を含んだものであり，簡単に求めることができないことを示しています．実験技術的にも渦度やレイノルズ応力の空間微分項を解析対象全体において考えなくてはならないという問題があります．
Lighthill方程式を直接解くことは難しそうですが，音源項に課題がまとめられていることから，空力音を予測するひとつの方法として，実験や解析によって音源項を算出して，音場は別に解析する分離解法が開発されてきました．分離解法として最も利用されているのがLighthill-Curleの理論及びFfowcs-Williams and Hawkingsの理論(8)です．
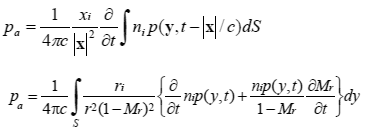
式の細かい説明は省略しますが，流れ場の非定常運動によって流れの中に置かれた物体の表面に圧力変動が誘起され，その圧力変動の時間微分が音として遠方に伝播するというものです．図3(a)は加藤千幸先生ら(9)によってLighthill-Curleの理論を用いて計算された円柱から放射される空力音スペクトルの計算結果です．また，図3(b)は筆者ら(10)によって円柱表面の圧力変動を元に空力音を推定した結果です．いずれの結果もLighthill-Curleの理論を用いて空力音の予測が可能であることを示しています．
Lighthill-Curleの理論を用いて空力音の解析を行うことの利点は，数値解析では一般に物体近傍には細かいメッシュが切られていることが多いので，物体近傍では解析の解像度が高いことがあげられます．後述するように渦音の理論を用いる場合は，解析領域全体の空間積分が必要となるため，メッシュの粗さの問題が解析精度に影響を与えることも多いからです．
Lighthill-Culreの理論では音源項を空間積分項から表面積分項に変換してあるため，高い解析精度が得られるという利点があります．また，実験について考えてみると，近年では時系列感圧塗料の開発が急ピッチに進められているので，この技術を活用すれば，Lighthill-Curleの理論によって空力音を実験的に予測できるようになると考えられます．たとえば，東北大の浅井圭介先生のグループの研究(11)を応用して円柱や角柱から放射される音の予測や将来的にはファン騒音の予測に利用できるのでないかと期待しています．
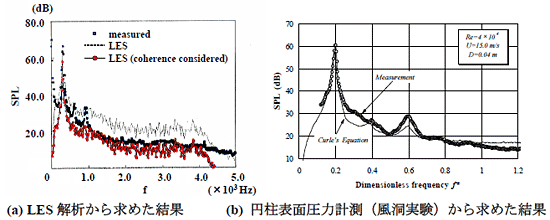
図3 Lighthill-Curleの理論を用いて円柱からの空力音スペクトルを予測した結果
Lighthill-Curleの理論は音の予測という面では実験・解析ともに適していますが，流れ場と音との関係が直接的ではないという問題も残されています．特に企業などで空力音を低減する課題に取り組んでいる技術者からは，流れ場をどのように変えたら，音がどの程度変わるのかを知りたいという要望が強いことから，Lighthill-Curleの理論だけでは不十分です．そこで流れ場の空間積分項を含むため，解析規模や精度の面では不利になるのですが，Powellの渦音の理論やLighthillテンソルを用いた音響計算が行なわれています．
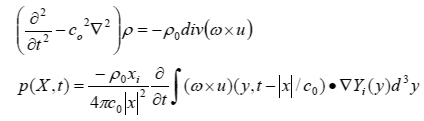
図4(a)は角柱から放射される空力音をLighthillテンソルを音源項として求めた結果です． 図4(b)のCurleの理論を用いた解析結果と比較すると，渦列の音場への干渉，ドップラー効果による音場の変化（Curleの理論ではドップラー効果の影響は出てこない）などの違いが生じていることがわかります．図5に示す音源項の結果から，角柱の前側の角部やカルマン渦の形成領域に強い音源が見られることもわかります．Lighthillテンソルを用いて音場解析を行う場合，音響解析を周波数領域で解析するため，多くの周波数領域のデータを見たい場合などは解析を複数行わなければならないこと，空力音解析の場合，音源となる渦の大きさが音のスケールに比べて小さいため，音響解析としては（波長を捉えるには十分な格子サイズ以上の）非常に細かいメッシュが必要となり，解析規模がかなり大きくなるという欠点はありますが，流れ場からの音の放射の詳細を知るには優れた手法であることがわかります．
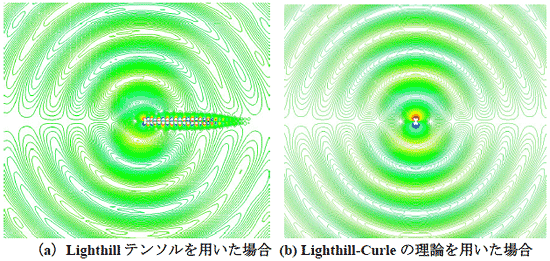
図４ 角柱から放射される空力音解析結果
図5 角柱周りの音源項の分布（Lighthillテンソル）
渦音の理論を実験で確認することは，渦度分布を時系列で計測しなければならないという問題から非常に難しい課題です．過去に著者は，円柱後流の渦度変動と物体表面の圧力変動の相互相関を計測し，空力音に寄与する渦度変動を抽出することを試み，カルマン渦の形成領域において空力音が発生すること(12)を明らかにしましたが，従来の熱線流速計を用いた計測では，条件付抽出法が可能なケースに限定されていました．この問題を九州大学の速水洋先生，東京大学の岡本 孝司先生に相談したところ，ダイナミックPIVの利用を進められ，ダイナミックPIVを活用することによって，円柱後流から放射される音を渦音の理論を用いて予測できることを確認しました(13)(14)（詳しくは鉄道総研宇田東樹さんの記事を参照してください）．感圧塗料とダイナミックPIVは今後，空力音に関する実験研究を進めるにあたり非常に有効なツールになると筆者は考えています．
直接解法
自動車メーカーと共同研究を進めていると流れと音が連成した空力自動音の課題が多いことに気がつきます．実際に製品になるときには対策が講じられているため，製品でこういった空力音響共鳴音を耳にすることはないようですが，設計段階ではいろいろと苦労されているようです．先にあげた分離解法では流れ場と音場を別々に計算するため流れと音の相互干渉によって発生する音場を解くことはできません．この場合，圧縮性のNS方程式を解いて，圧力場（密度場）を直接計算する直接解法を用いる必要があります．
航空機やロケットなどでは飛行マッハ数が高いことから圧縮性流れ解析を行うことが一般的ですが，自動車などではマッハ数が低いため，圧縮性の流れ解析を精度良く行なうことが難しい場合があります．マッハ数が小さいということは流れ場と音場の代表速度の比が大きくことなることを示しており，音速を解析の代表速度と見なして時間スケールを無次元化すると流れ場からみたタイムステップは非常に小さなものとなります．このため，低マッハ数の圧縮性解析では膨大なタイムステップの解析が必要となります．同じ理由で解析領域の大きさも課題となります．特に音響解析の外部境界では境界面での音の反射を抑える必要があります．無反射境界が開発されていますが，境界の扱いによっては計算誤差が大きくなる場合があるようです．
低マッハ数の圧縮性解析では計算が不安定になることを抑えるために，NS方程式を高次Favreフィルターによって平均化処理し，空間微係数に高次精度のコンパクトスキームを用いるのが一般的です．たとえばドアミラーやキャビティからの音の直接計算では，空間微係数には6次精度のコンパクトスキームと時間発展には3次のRunge-Kutta法が用いられ，NS方程式には10次精度のフィルターが使用されています (15)(16)．
図6は同僚の横山博史先生が計算したキャビティ周りの流れと音の直接解析の結果です．圧縮性NS方程式を直接解くことにより，渦がキャビティに衝突した際の膨張波の発生メカニズムやキャビティ周りの音場が明らかとなりました．しかし， NS方程式を高次フィルターを用いて解析するため，解析には構造格子を使用しているので，複雑形状を解析対象とする場合に課題が残されています．自動車メーカーでは設計CADから格子を迅速に作成し，複雑形状から放射される空力音の解析が必要とされているので，メッシュ作成，解析精度などについては今後解決していく必要があります．現在，自動車メーカーでは格子ボルツマン法を用いた音場解析などの新しい試みも取り入れられており，この分野の計算手法のさらなる高度化が求められています．
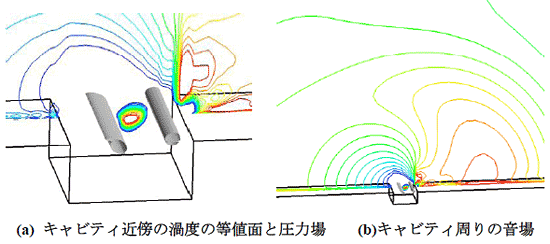図6 キャビティ周りの流れ放射される空力音
終わりに
分離解法と直接解法による空力音解析や空力音の実験技術の事例を紹介しました．解析技術，実験技術ともにこの10年で大きく発展しています．物体後流の音源部分の解析や計測が可能となりつつあります．また，空力音響共鳴音解析も可能となりました．ところが，最初に取り上げたマジックパイプのような簡単な問題でも，まだまだ課題は残されています．一つのキャビティを計算することはできても，数十個のキャビティともなると（リソースのことを考えると）まだまだ難しいようです．あるいは，キャビティ端部の小さな曲面部の流れから出る音，流路自体が変形，回転（移動），振動している場合の音を計算するのは，計算機のリソースの問題も含めて容易ではありません．今回は触れませんでしたが，たとえばパイプの壁面を透過する音の問題，パイプの表面が空力及び音響加振によって振動した場合の音についても十分な精度で解析できるようになっているとは言えない状況です．マジックパイプの音の物理を解明するにはまだまだ道は遠いようです．しかし，マジックパイプの音をリアルタイムでバーチャル空間で解析できるようになれば，自動車や新幹線の車内音，ファンを音源とする電子機器の騒音などの解析や低騒音化が可能になると思われます．流体解析，音響解析，振動解析そしてできれば音響心理学を組み合わせた“空力音響解析”に取り組んで見ませんか？
参考文献