Drop on intended target 1

Let's take a look!

What type of experiment is this?

Experimental procedure and explanation:

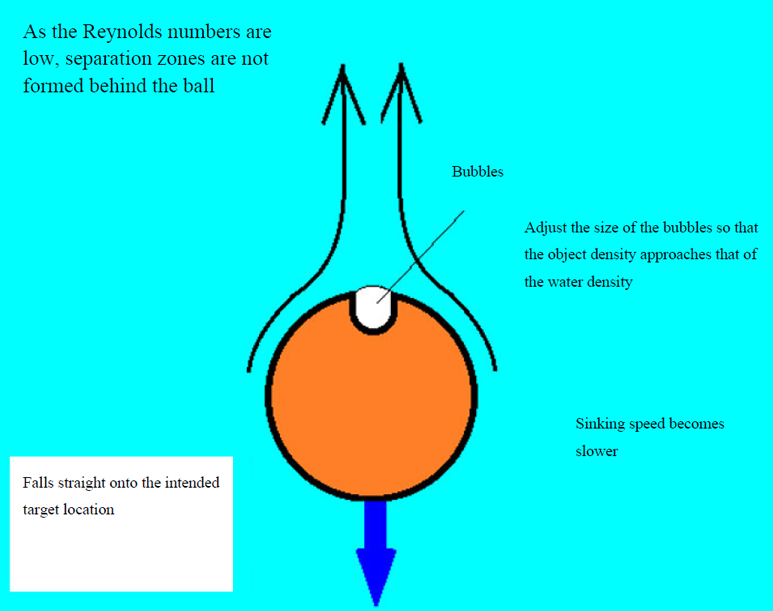
• A plastic ball is submerged in the water and dropped onto the intended target.
• The plastic ball, 6 mm in diameter and 0.12 g in mass, is used is a toy air gun bullet. A pin vise is used to make a small hole that is approximately 1-mm deep and 2-mm in diameter. When placed in water, air bubbles remain there. The average density (density = mass / volume) should be slightly greater than that of water (to ensure that it sinks slowly) and as close to the density of water as possible. If this is done, the speed at which the plastic sphere sinks (settling speed) will be very slow.
• In this case, the Reynolds number Re becomes very small, and the effect of viscosity becomes strong, which prevents the formation of a separation vortex behind the sphere. The Reynolds number Re can be calculated using the following equation
  Re = U L /ν
  Let U be the settling velocity [m/s], L be the representative length [m] (standard dimension, diameter for a sphere), and ν be the kinematic viscosity of the fluid (for water at room temperature, approximately 10^-6 m²/s ) of the fluid.
• If the Reynolds number Re is less than 1, the effect of viscosity becomes very strong, and no separation vortex is generated. Further, at a value less than 10, asymmetric separation vortices do not form and do not shake much.
• Under the conditions of this video, Re <10, the ball does not shake and seems to have fallen straight on its target.
• One way to sink an object straight down is to make the average density of the object close to the density of the liquid such that the settling velocity is very small.
• This experimental video was produced with the support of JSPS Grant-in-Aid for Scientific Research 18K03956.

[Keywords]	Separation vortex, density, Reynolds number
[Related items]	They don't fall where intended, Drop on intended target 2
[Reference]	Ryozo Ishiwata, "The Wonder of Flow," Kodansha Blue Backs, P16-21. Ryozo Ishiwata, "Illustrated Fluid Dynamics Trivia", Natsume Publishing, p. 28-29.

◀　Back Next　▶