Accuracy improvement of the Cartesian grid method for numerical simulations of heat transfer and fluid flow
Abstract
The Cartesian grid methods are one of the methods increasingly employed for practical applications in the area of computational fluid dynamics because of their advantage in facilitating mesh generation for complex geometries. However, in most of their methods, some interpolation/extrapolation procedures smearing the interface are employed (Fig.1 (a)), which may yield deterioration in accuracy especially under low grid resolution cases. We have proposed a new discretization scheme on Cartesian grids, namely, a “consistent direct discretization approach” (Fig.1 (b)) for heat transfer and fluid flow problems. Being different from conventional approaches with smeared interface, the governing equations are discretized directly even in the immediate vicinity of the solid boundary. Also, in their discretized equations, the velocity-pressure consistency, which is essential for incompressible flow simulations, is properly considered. As for thermal field, treatments for various types of thermal boundary conditions are proposed: Dirichlet (isothermal) and Neumann (adiabatic/iso-heat-flux) boundary conditions for convective heat transfer, and a fluid-solid thermal interaction for conjugate heat transfer.
Simulations in some fundamental problems are demonstrated to assess the validity and applicability of the present method. It is confirmed that the present method significantly improves accuracy for the flow and thermal fields under respective types of boundary conditions (e.g. Fig. 2 (a)). Especially, the flow fields predicted by the present scheme are less sensitive to the Courant number owing to the consistency between the Navier-Stokes and pressure Poisson equations (Fig. 2 (b)). In conjugate heat transfer problems, since the energy equations for both fluid and solid phases are discretized directly while satisfying the thermal relations that should be valid at their interface, the spatial accuracy and numerical stability are maintained even under severe conditions of high physical property ratios between fluid and solid phases reflecting practical materials (Fig. 3).
It is expected that the use of the present method allows precise prediction and better understanding of flow and thermal phenomena observed in industrial applications.
Keywords
Cartesian grid method, incompressible flow, convective heat transfer, conjugate heat transfer, immersed boundary
Figures
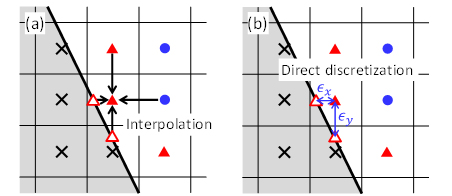
Figure 1. Comparisons of Cartesian grid methods:
(a) Direct forcing immersed boundary method, (b) Present method.
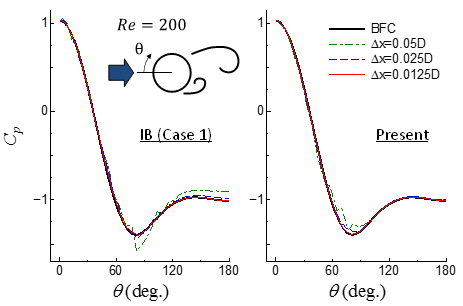
(a) Time-averaged pressure distributions on a cylinder surface.
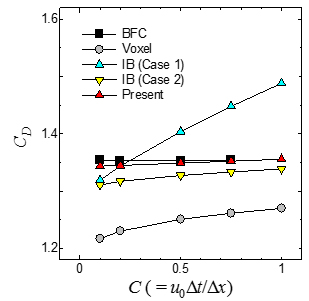
(b) Dependence of the drag force coefficient on the Courant number.
Figure 2. Verifications in the flow around a circular cylinder.
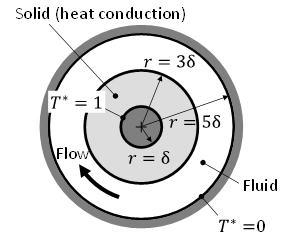
(a) Schematic diagram.
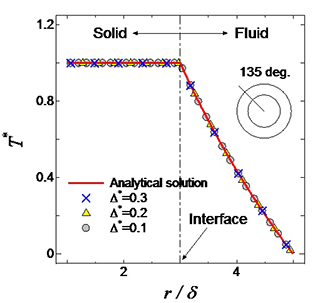
(b) Temperature profiles in the radial direction.
Figure 3. Verifications in the flow channel between concentric cylindrical walls with solid heat conduction (cupper to air system).


