Development of numerical method for mass transfer from a buoyant bubble under a high Schmidt number condition

Rihito ADACHI Osaka University, currently Mitsubishi Electric Corporation	Takeshi OMORI Osaka University	Takeo KAJISHIMA Osaka University

Abstract

Under a high Schmidt number condition, concentration boundary layers get much thinner than momentum boundary layers. Resolution requirement to numerically capture the steep concentration gradient near an interface is therefore significantly high. This article presents a novel VOF-based method to predict mass transfer from gas-liquid interfaces using a computational grid of a marginal resolution required for the solution of the Navier-Stokes equation. The solution procedure to the mass conservation equation is divided into two steps: the dissolution and diffusion step and the advection step. The concentration profiles near gas-liquid interfaces, which are identified as segments (in case of two-dimensional computations) in each computational cell, are reconstructed in terms of the complementary error function by virtue of the boundary layer approximation to the solution of the unsteady advection-diffusion equation of mass. The amount of dissolution from the interfaces and diffusion in the vicinity of the interfaces is obtained by taking advantage of the reconstructed concentration profile on each interface segment. In the advection step, the un-smoothness of concentration profiles in the interface cells is explicitly taken into consideration by taking full advantage of a VOF advection scheme. The present method is validated in two-dimensional test problems: gas diffusion from the static bubble (Figs. 1 and 2) and the mass transfer from a freely rising buoyant bubble (Tab. 1 and Figs. 3 to 5). The validation shows the present method is capable of resolving a concentration boundary layer which is as thin as a computational cell. The reduction rate in the overall computational cost is O(10^-3) compared to one of our previous DNS-based methods (Ezu et al., 2011) without the subgrid-scale resolution.

Key words

Computational fluid dynamics, Multiphase flow, Volume-of-fluid method, Bubble, Mass transfer

Figures

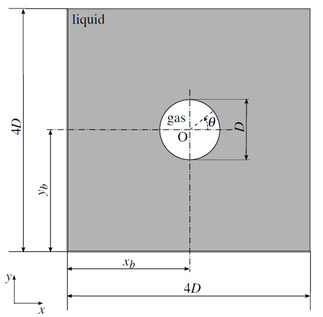
Fig. 1 Computational domain for the time-dependent diffusion problem: Gaseous phase is centered at .  for Case 1 and  for Case2.

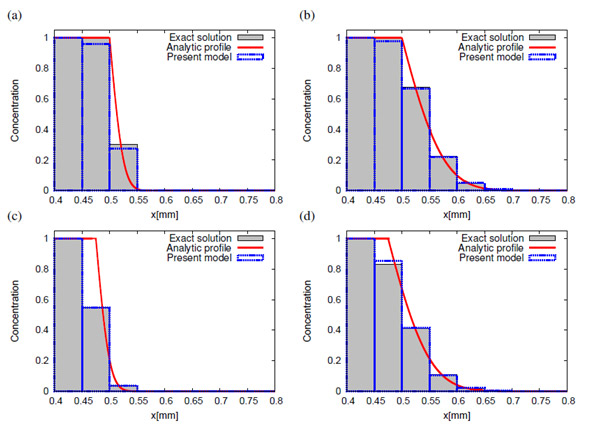
Fig. 2 Concentration profiles of the exact solution and the present numerical solution on the horizontal line passing through the bubble center, for the diffusion problem. The solid lines show the analytic profile, the solid line boxes show the cell averaged concentration values of the analytic solution and the dashed line boxes show the cell averaged concentration values calculated from the present model. (a) and (b) show the case that gas-liquid interface is at (Case 1). (c) and (d) show the case that gas-liquid interface is at (Case 2).

Tab. 1 Numerical parameters.

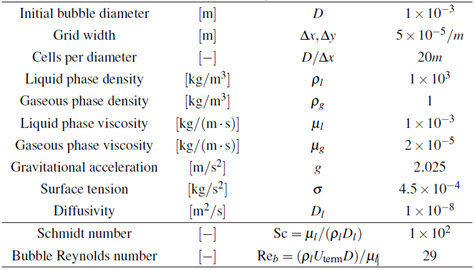
Fig. 3 Computational domain and the initial bubble shape and position for the mass transfer problem. Slip wall conditions are imposed on all boundaries.

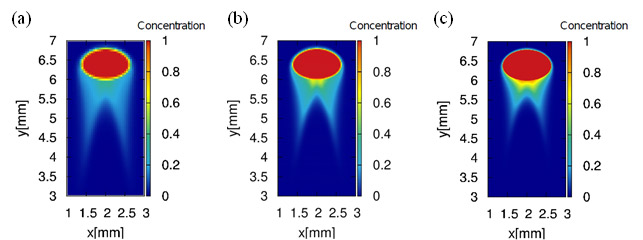
Fig. 4 Concentration distribution of the dissolved gas in the liquid phase in the steady state: (a) present model, 20 cells per bubble diameter, (b) present model, 40 cells per bubble diameter, (c) our DNS-based previous model, 240 cells per bubble diameter.

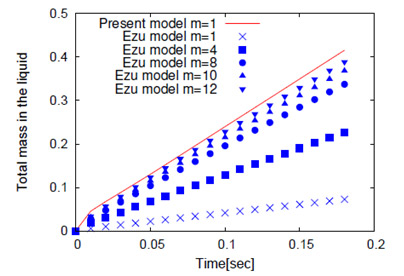
Fig. 5 Total amount of gas dissolved from the buoyant bubble normalized by the initial amount of gas in the The solid line shows the result by the present model and the symbols by our previous DNS-based model. “” indicates the number of cells per bubble diameter, divided by 20.