流れ 2014年1月号 目次
― 特集テーマ:流体工学部門講演会 ―
| リンク一覧にもどる | |
回転チャネル乱流中に発生する大規模間欠構造の強化と減衰
石田貴大 |
1.はじめに
第91期機械学会流体工学部門講演会において研究発表を行い,光栄にも優秀講演賞を頂きました.ここではご評価を頂いた発表内容である,系の回転を伴う平面チャネル流中の乱流遷移現象について紹介させていただきます.
多くの方がご存じのように私たちの身の周りで生じている流れのほとんどは乱流と層流に大別されます.しかし,この二つの流れを完全に分類することはこれまで困難と考えられており,乱流制御を実現する上で乱流と層流での境にある遷移域での現象を解明することは必須とされてきました.遷移現象の研究はレイノルズによる円管内流の先駆的実験からはじまり,彼は遷移域で局在した乱れである乱流パフが発生することを発見しました[1].その後,一世紀以上の年月を経ながら層流と乱流の境界は円管直径と平均流速からなるレイノルズ数で1700~2300程度と,厳密な臨界値は定まっていませんでした.しかし,近年の研究の進展により,乱流パフの有限寿命を考えることで生存時間と分裂時間を特定し,乱れの統計的平衡状態を導き出すことで,臨界レイノルズ数が2040±10と決まるなど[2],遷移現象の解明が急速に進みつつあります.
遷移レイノルズ数域(亜臨界遷移)における乱れが空間的に局在する構造の発生は円管内流のみでなく,流れの形態に関わらず平行平板の間を流れるポアズイユ流(チャネル流)[3]やクエット流[4]においても発生することが示されています.この構造は,乱流パフとは異なり,主流方向に対して傾いた乱流域が縞模様を呈することから乱流縞と呼ばれており,臨界値の特定(クエット流)[5]や外力による影響[6]など,様々な面からの研究が盛んに行われております.
本研究では乱流縞の発生するチャネル遷移流にスパン方向軸に対して回転を加えた流れ場(Rotating Plane Poiseuille Flow, RPPF)を解析対象(図1)とし,直接数値解析によって大規模乱流構造とそれに伴った統計量の変化を解析してきました[7].今回は乱流縞の詳細と微小回転数効果及び高回転数効果について簡単に紹介いたします.
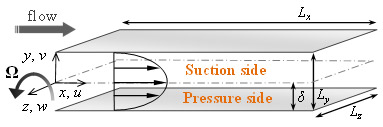
Fig. 1 Configuration of rotating Poiseuille flow.
2.大規模遷移構造―乱流縞
図2にはRPPFで発生した乱流縞の3次元可視化図を示しています(レイノルズ数:Reτ = uτδ/ν = 64,回転数:Roτ = 2Ωδ/uτ = 0.02,uτ:壁面摩擦速度,δ:チャネル半幅,Ω:角速度).速度に関しては,ui = Ui + u’iとして平均値Uiと変動量u’iに分類して示します.乱流縞は高速・低速領域の境である渦構造が密集した速度の遅い乱流域と,乱流の微細渦がほとんどない速度の速い準層流域とが交互に傾いて発生する大規模乱流構造で特徴付けられます.簡単のため,図3にチャネル中央(y = 0)での乱流縞のx-z平面での模式図と,図中の黒点線上(z = 0)の位置の速度の変化を示します.乱流縞の維持過程は速度の速い準層流域が速度の遅い乱流域に衝突することで速度が急激に減少します.その後,流体は速度の遅い乱流域から速度の速い準層流域に向かうため,一部で加速区間が生じます.これらの流れを主流方向に繰り返すことで,流れに局所的な高速領域と低速領域が現れ,衝突による速度の減少により,低速ストリークが卓越して観察され,乱流域の渦構造が多く発生します.このように乱流と層流の遷移過程において層流へと完全には遷移せずに,局在した乱れの生成を繰り返すことで乱流縞は維持しています.
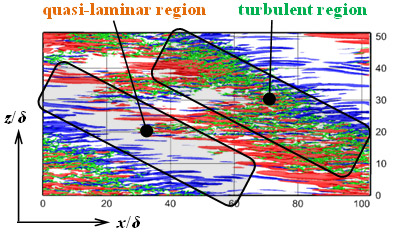
Fig. 2 Visualization of instantaneous flow field at Reτ (= uτδ/ν) = 64 and Roτ (= 2Ωδ/uτ) = 0.02, in an (x, z)-plane. Red isosurface, u’/uτ> 3.5, blue, u’/uτ< –3.5, green, II’+ = u’i,ju’j,i < –0.015 (which is equivalent to the vortical position). The mean flow moves from left to right.
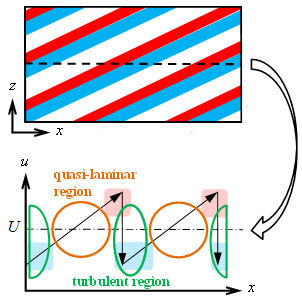
Fig. 3 Diagram of the structure of turbulent stripe and the streamwise velocity. Red and blue region represents high- and low-speed regions, respectively. Orange and blue circle notes quasi-laminar and turbulent regions, respectively.
乱流縞の特徴として,その構造が主流方向に対して傾きを持つことから乱流域に沿った平均速度を持つスパン方向二次流れを形成することが挙げられます.図4にはRPPFにおける乱流縞発生下での(a)主流u’,(b)壁面垂直v’,及び(c)スパン方向変動速度w’の空間分布を示しています.乱流域の特定には壁面垂直方向変動速度が有効であり,乱流域が間欠的に発生(図4(b))しており,図3でも示したように高速・低速ストリークが乱流域の上流・下流にそれぞれ発生します(図4(a)).ここでスパン方向成分に注目すると,図4(b)で示される乱流域に沿うような形で正負の速度変動が発生し,スパン方向二次流れを形成していることが分かります.
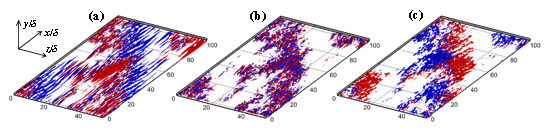
Fig. 4 Visualization of instantaneous flow field at Reτ= 64 and Roτ= 0.015. (a) Red isosurface, u’/uτ> 3.5; blue, u’/uτ< -3.5, (b) Red isosurface, v’/uτ> 0.75; blue, v’/uτ< -0.75, (c) Red isosurface, w’/uτ> 1.5; blue, w’/uτ< -1,5. The mean flow move from left below to upper right.
3.乱流縞の強化と減衰
前節では可視化結果から,乱流縞が特徴的な流れ場を形成することを示しました.次に,乱流縞の持つ統計的性質を紹介していきます.
図5にスパン方向平均速度Wと変動速度のひずみ度S(w’)を示します.一般的に,乱流や層流状態のチャネル流ではこれらの統計量はゼロとなりますが,乱流縞の発生する静止系では明らかに平均速度Wはチャネル中央が,ひずみ度S(w’)では壁面近傍で顕著な高い値を示します.これらは乱流縞がスパン方向二次流れを形成し,非対称性を生じさせることが確かめられます.注目すべきは微小回転下での分布を見ると,静止系に比べて飛躍的に値が増加しており,乱流縞特有のスパン方向二次流れが強化されていることです.これに対して,さらに回転数が増加していくと,各統計量は次第に減少し,最終的にはゼロに漸近していきます.これは,高回転下では回転系特有の流れ方向に伸びた秩序縦渦構造[8]が支配的となる一方で,スパン方向の非対称性をもたらす乱流縞が減衰したことを表しています.
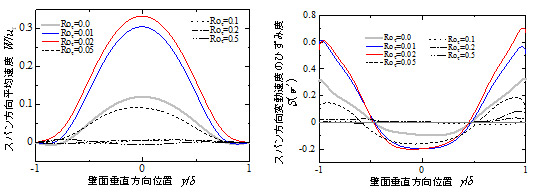
Fig. 5 Spanwise mean velocity profile and skewness factor of w’ at Reτ = 64
for various rotation number.
4.終わりに
今回紹介させて頂いた,遷移域において発生する乱流縞構造は物質や熱輸送を強化するうえで有効となります.層流状態の流れ場では熱・物質輸送係数が極めて小さいですが,乱流縞の作用により輸送係数を飛躍的に向上することができます.さらに,乱流状態でも見られない,特徴的なスパン方向速度を持つことにより,スカラー量のスパン方向への効果的な輸送が行われます.加えて機器の形態を変えることなく,回転数の制御のみによって,微小回転数下では乱流縞を強化し,スパン方向速度成分の増加を実現でき,高回転数下では乱流縞が減衰し,秩序縦渦構造が発生することによって回転系特有の流れ場が形成し,流れ場の流動特性を大きく変えることができます.今後も工学的にユニークな応用展開ができると考えています.
ニュースレターを通して,遷移域での現象及び回転系乱流に一人でも多くの方に興味を持っていただければ幸いです.
最後となりましたが,ニュースレター執筆の機会を与えてくださった日本機械学会の関係者の皆様,ならびにこの度の受賞に至るまで指導してくださった東京理科大学 塚原隆裕 講師,及び川口靖夫 教授に深く感謝いたします.
参考文献


