流れ 2014年1月号 目次
― 特集テーマ:流体工学部門講演会 ―
| リンク一覧にもどる | |
乱流・非乱流界面近傍の反応場に関する研究
|
1.はじめに
乱流により物質が混合されながら化学反応する現象は燃焼器,反応器などの工業装置内や汚染物質の環境中への拡散などさまざまな分野にみられる.そのため,化学反応を伴う乱流現象の解明や予測手法の確立は工学的に重要な課題のひとつとなっている.噴流や後流などのせん断流れにおいて,乱流流体と非乱流流体の混合は乱流・非乱流の界面近傍において乱流流体が非乱流流体を取り込むことで生じる.反応物質が乱流流体と非乱流流体に別々に含まれる場合,乱流・非乱流界面近傍で反応物質の混合と化学反応が進行し,乱流の発達と共に生成物質が拡散する.そのため,乱流・非乱流界面の性質や界面近傍での混合・反応場の特性が乱流中で生じる化学反応に対して大きな影響を与えると考えられる.
近年,乱流・非乱流界面近についての研究が多くなされており(1)(2),界面近傍の渦の性質や界面を通した流体の取り込みなどさまざまな性質が明らかにされつつある(3)(4)(5).しかし,乱流・非乱流界面近傍の化学反応に着目した研究例はほとんど無く,乱流・非乱流界面近傍の反応場の性質には未解明な部分が多く残されている.濃度変動の最小スケールはシュミット数の増加と共に小さくなる.シュミット数が小さい気相における反応場に対してはDNSによる解析が有効である.しかし,液相の反応場ではシュミット数が大きいためDNSでの解析が困難となる.そのため,液相の反応場の特性の解明には実験による反応性物質の濃度計測を行うことが重要である.そこで,我々は液相における乱流・非乱流界面近傍の反応場の特性を明らかにすることを目的として実験を行っている.
本稿では第91期流体工学部門講演会にて発表した,化学反応を伴う液相二次元噴流の乱流・非乱流界面近傍の濃度統計量に関する研究について紹介する.
2.実験について
図1に本研究で対象とする二次元噴流の概略図を示す.噴流中(出口幅d = 2.0 mm,出口流速UJ = 1.29 m/s)に反応物質A(初期濃度ΓA0 = 0.4 mol/m3)が含まれており,周囲流中(平均流速UA = 0.061 m/s)に反応物質B(初期濃度ΓB0 = 0.2 mol/m3)が含まれている.噴流場においてA + B → Rにより表される二次の化学反応が生じる.物質A, Bは無色であり,物質Rは赤色である.また,噴流中には化学反応に影響を与えない青色の染料Cが含まれている.レイノルズ数Re = (UJ-UA)d/ν ≅ 2,200,シュミット数はSc ≅ 600,流れ場の時間スケールの化学反応の時間スケールに対する比であるダムケラ数はDa = k(ΓA0 + ΓB0)d/(UJ-UA) = 11.7である.ここでνは動粘度,kは反応速度定数である.
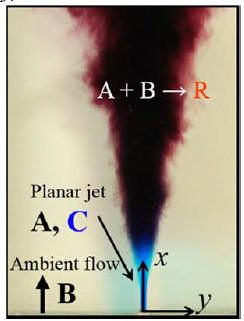
Fig. 1 Snapshot of reactive planar liquid jet.
染料である物質Rおよび物質Cの瞬時濃度を吸光スペクトル法(6)に基づく光ファイバプローブにより測定した.さらに,保存スカラ理論(7)を適用し,物質R, Cの瞬時濃度を用いて物質A, Bの瞬時濃度を算出した.
乱流・非乱流界面を検出するためには乱流領域と非乱流領域の判別が必要である.乱流領域と非乱流領域との差異は渦度の有無により定義されるが,現状の計測技術では渦度を精度よく計測することは非常に困難である.そこで,本研究では乱流・非乱流流体を判別するために,噴流とともに拡散するスカラ量を利用する方法を用いた.濃度や温度などのスカラ量を乱流領域の指標として用いた研究として,Antoniaによる研究(8)やWesterweelらによる研究(2)が挙げられる.本研究では噴流に含まれる物質Cの濃度を乱流領域の指標として利用し,物質Cの瞬時濃度がある閾値より高い瞬間を乱流,低い瞬間を非乱流とした.
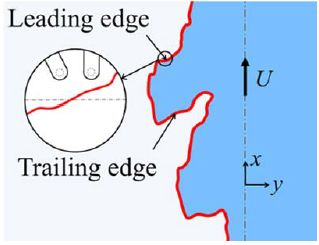
Fig. 2 Schematic diagram of the turbulent/non-turbulent interface of a jet.
図2に乱流・非乱流界面の概略図を示す.本研究では,流れ方向に垂直な界面(Leading edgeおよびTrailing edge)に注目して考察を行った.二つの界面の検出はy方向に並べた二本の光ファイバプローブにより行った.二本のプローブが非乱流領域から乱流領域への変化を同時に検出した瞬間をLeading edge,乱流領域から非乱流領域への変化を同時に検出した瞬間をTrailing edgeとした.そして,これらの界面を検出した時刻から経過した時間で条件付けした濃度統計量を算出した.
3.実験結果
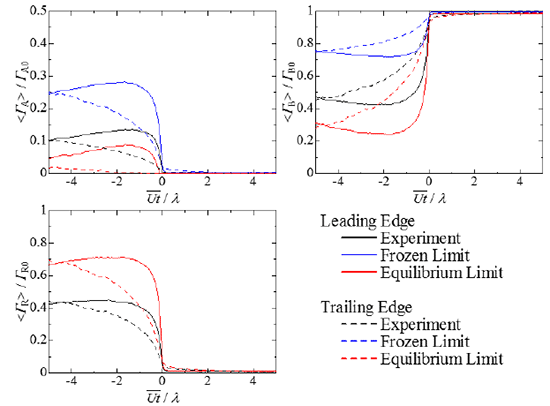
Fig. 3 Conditional mean concentrations at x/d = 20.
図3にx/d = 20におけるLeading edgeおよびTrailing edge近傍での反応物質A, Bおよび生成物質Rの条件付き平均濃度<ΓA>, <ΓB>, <ΓR>を示す.また,図中にはDa → ∞とした極限(Equilibrium limit)での値とDa = 0とした極限(Frozen limit)での値がともに示されている.縦軸は各物質の初期濃度ΓA0, ΓB0および代表濃度ΓR0 = ΓA0ΓB0/ (ΓA0 + ΓB0) によって無次元化されている.横軸は界面を検出した時刻を0とした時間tを表し,測定位置での時間平均流速Uとテイラーマイクロスケールλによって無次元化されている.なお, Trailing edge近傍との比較のためにLeading edge近傍での結果の横軸を反転して表示してあり,図中のt < 0が乱流領域を,t > 0が非乱流領域を表している.
各物質の濃度は界面近傍の-1 < Ut/λ < 0の範囲で大きく変化し,濃度変化の傾きは,Trailing edge近傍よりLeading edge近傍においてより急峻であることがわかる.また,濃度変化の幅は物質A,B,Rに対してほぼ同じであり,Da = 0,Da = 11.7,Da → ∞に対してもほとんど変化がない.したがって,条件付平均濃度が大きく変化する幅は化学種や反応速度によらずほぼ同一であることがわかる.図中のt>0では物質A,Rの濃度がほぼ0となっており,これらの物質は非乱流領域にほとんど存在していないことが確認できる.また,非乱流領域では物質Bの濃度が初期濃度とほぼ等しくなっており,反応による濃度変化が生じていないことがわかる.一方,無反応極限での濃度との比較から,乱流領域では反応により反応物質の濃度が減少していることがわかる.したがって,乱流領域に物質Bが取り込まれた後に反応が進行していると考えられる.
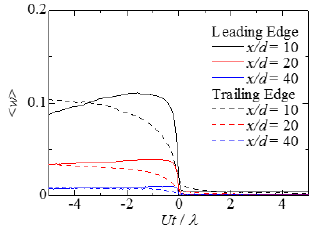
Fig. 4 Conditional mean chemical reaction rate.
図4にx/d = 10, 20, 40での条件付き平均反応速度<w>を示す.wは物質Rの生成速度kΓAΓBをUJ,UA,dおよびΓA0, ΓB0で無次元化したもので,w = DaΓAΓB / (ΓA0ΓB0)で定義される.図より非乱流中での反応速度はほぼ0であり,界面から乱流領域に向かって<w>は大きく増加することがわかる.このことからも,界面近傍での化学反応は周囲流体中の物質Bが乱流中に取り込まれた後に乱流中で生じていることがわかる.乱流領域での<w>は下流に向かうにつれて減少し,x/d = 40での<w>は非常に小さい値となる.これは反応の進行により物質Aが消費され界面近傍での物質Aの濃度が小さくなるためである.界面近傍での<w>の増加の傾きはTrailing edge近傍よりLeading edge近傍において大きい.また,Leading edge近傍での反応速度はTrailing edge近傍よりも大きくなっている.したがって,Trailing edge近傍よりLeading edge近傍において反応の進行がより活発であると考えられる.
4.おわりに
本稿では反応を伴う液相二次元噴流を対象として実験を行い,乱流・非乱流界面近傍の反応場について調査した結果を紹介した.結果より,乱流・非乱流界面近傍の反応場は界面の向きに依存することがわかった.
本稿で紹介した実験は濃度統計量にのみ注目している.今後は,濃度と速度の同時測定を行い,物質の輸送などと関連付けて界面近傍の反応場の性質の解明に取り組みたい.
謝辞
本研究の一部は科研費 (25002531,25289030,25289031,25630052) の援助を受けて行われた.記して謝意を表する.
参考文献







