流れ　2016年11月号　目次

―　特集テーマ：2016年度年次大会　― 巻頭言 （藤井，横山，渡辺） 市場にデビューする相反転方式ターボ機械 金元敏明（佐賀大学） 非平衡格子乱流場の特性とスカラー輸送機構 酒井康彦，長田孝二, 伊藤靖仁, 渡邉智昭, 岩野耕始（名古屋大学） ワークショップ：複雑流体の新展開 山本剛宏（大阪電気通信大学），鳴海敬倫（新潟大学），蝶野成臣（高知工科大学） 複雑流体としての生物系粒子分散系 山本剛宏（大阪電気通信大学） 非アファイン性を考慮した高分子添加溶液におけるエネルギー伝達と抵抗低減 －働く高分子と働かない高分子－ 堀内潔（東京工業大学） EFDワークショップ：光学的流体計測手法 渕脇正樹（九州工業大学），飯尾昭一郎（信州大学），稲澤歩（首都大学東京），菊地聡（岐阜大学） 多レンズ多方向光学系の設計および瞬間CT法による非定常流体現象の三次元計測と３Dプリンティング 石野洋二郎（名古屋工業大学） 非定常熱流動場における壁近傍の速度-熱伝達の光学的同時計測について 山田俊輔（防衛大学校），中村元（防衛大学校） 　｜　リンク一覧にもどる　｜

 

非平衡格子乱流場の特性とスカラー輸送機構

酒井 康彦 名古屋大学 長田 孝二 伊藤 靖仁 渡邉 智昭 岩野 耕始

1.　緒　　　言
一般に，乱流のレイノルズ数が高い場合，単位質量あたりの散逸率に関して次式のような基本的な性質があると信じられている．　　

　 　　（1）

ここで，L_uは乱流の積分スケール，u'は変動速度ｒｍｓ値，C_εは係数である．この関係式は乱流の運動エネルギが大きなスケールから小さなスケールに輸送される時に，途中の波数間でのエネルギフラックスが一定であり，それがεとバランスする（平衡する）場合に成立し，C_εは乱流の種類によらない普遍定数と考えられてきた⁽¹⁾．通常，このエネルギの流れをRichardson-Kolmogorov カスケードと呼び，式(1)を乱流の第ゼロ法則と呼ぶことがある⁽²⁾. しかしながら，最近英国Imperial College Londonの研究グループがフラクタル形状を持つ格子の下流の乱流を精密に調べた結果，C_εは普遍定数ではなく，乱流格子への流入レイノルズ数Re_M=U₀M/ν（U₀:流入速度，M：最大格子のメッシュ寸法，ν：動粘性係数）と乱流の局所のレイノルズ数Re_λ=u'λ/ν（λ：テイラーのマイクロスケール）によって，

　　　 (2)

となることが示された⁽³⁾．このような，所謂，非平衡乱流は，格子近傍に発生し，下流域の通常の平衡乱流とは著しい相違を示すことが明らかにされている．たとえば，
（１）格子近傍であるため乱れが著しく大きく，且つ減衰率が異常に大きいこと，
（２）積分スケールL_uとテイラースケールλの比が下流方向に一定であること，
（３）散逸εはu'³ではなく，u'²に比例すること，
（４）乱流が非平衡状態にあるにも関わらずエネルギスペクトルには平衡乱流の時に成り立つとされる-5/3乗則が現れること，
等である．この中で，特に（２）と（４）の性質は従来の乱流理論では説明できないものであり，現在，世界中で研究が活発に行われおり，著者らの研究グループでも精力的に研究しているが^(4),(5),(6)，いまだその現象の解明は出来ていない．また，（１）と（３）の性質は，工学的応用上重要な性質であり，たとえば，エネルギ散逸（損失）が小さく，乱れ強度の大きな乱流混合装置（ミキサー）の開発に通じるものであるが，実際上，これらの応用はほとんど行われていない．以上の状況を踏まえ，本稿では，格子乱流に的を絞り，どのような格子の配置が上記のような非平衡特性を発生させるのかという疑問に答えるべく，4種類で合計11の格子を使用して，その下流の乱流特性を調べた結果⁽⁷⁾を報告する．また，四角型フラクタル格子乱流中に発展するパッシブスカラー混合層の特性を調べ，その乱流輸送機構を陰的LESにより数値シミュレーションにより調査した結果⁽⁸⁾も報告する．

 

2.　格子形状の非平衡乱流への影響

2・1　風洞と格子

　図１(a),(b)に本研究で用いられた風洞の測定部の略図と実験に使用した格子を示す．使用した格子は，フラクタル要素の繰り返し数Nが1から4の四角型フラクタル格子（Fractal Grids: FGs），通常の正方格子(Regular Grids: RGs)，2つの正方格子を組み合わせた複合格子(Combined Regular Grids: CRGs)，大きな四角格子の周りに小さな正方格子を配置した准フラクタル格子(Quasi-Fractal Grids: QFGs)の4種類である．複合格子（CRGs）と准フラクタル格子（QFGs）の違いは，複合格子（CRGs）が単純にメッシュの異なる2種類の正方格子を組み合わせただけであるのに対して，准フラクタル格子（QFGs）は測定断面の中央に十字型の開放部が存在することである．

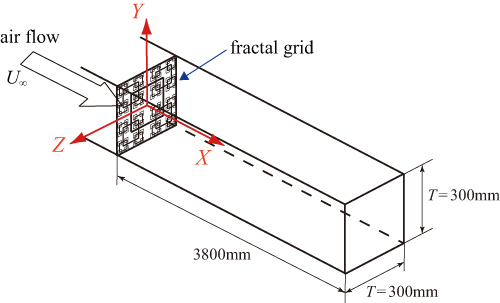
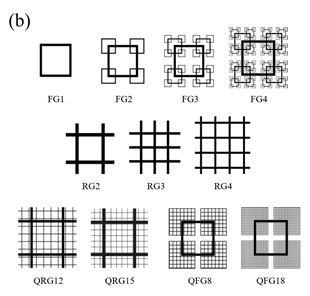
Fig.1　(a) Test section of wind tunnel and (b)test grids

2・2 測定結果

　図2に中心軸上におけるL_u/λとRe_λの関係を示す．図2(a)より，フラクタル格子乱流(FGs)の場合は繰り返し数Nが増加するにつれて，非平衡領域（L_u/λが一定の領域）が広くなることがわかる．正方格子(RGs)(図2(b))については，全体的に格子に近い領域（Re_λが大きい領域）で非平衡であり，格子から離れると（Re_λが小さくなると）平衡状態になる傾向があることがわかる．複合格子(CRGs)(図2(c))については，ほとんど平衡領域はみられない．一方，准フラクタル格子(QFGs)(図2(d))ではほとんどフラクタル格子(FGs,図2(a))と同様の分布を示していることがわかる．このことは，大きなスケールの格子と非一様に配置されたより小さな格子の組合せ（すなわち，中央の開放領域とその周りの遮蔽領域の存在）がより広い非平衡領域を生成する原因になっているものと予想される．

(a)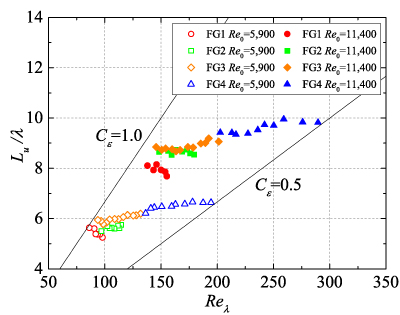
(b)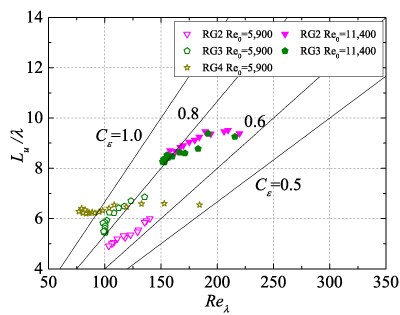
(c)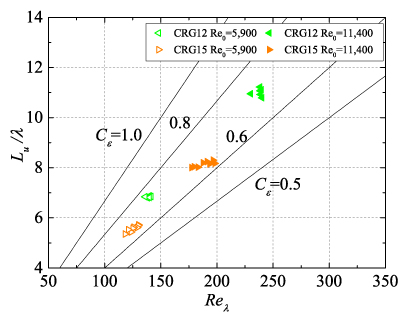
(d)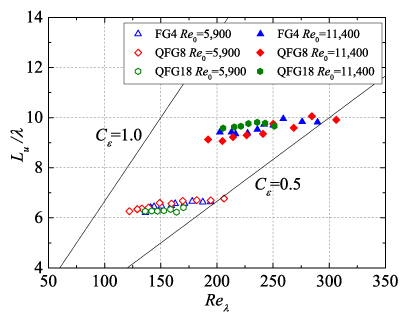

Fig.2　L_u/λ vs Re_λ  (a)FGs, (b)RGs, (c)CRGs, (d)FG4 and QFG

 

3.　四角型フラクタル格子乱流中のパッシブスカラー混合層の特性⁽⁸⁾

3・1　陰的LESによる混合層の計算

　本研究では，数値フィルターを使用した陰的ラージエディシミュレーション(Implicit Large Eddy Simulation: ILES)によって，フラクタル格子乱流中のパッシブスカラー混合層の計算を行った．使用した格子は繰り返し数Nが3の四角型フラクタル格子である．この格子は前章でのFG3に対応するものである．座標系の原点は格子中央にあり，流れ方向，鉛直上方向，スパン方向にそれぞれx，y，z軸を取る．各軸方向の瞬間速度をそれぞれu，v， wとする．レイノルズ数Re=U₀t₀/νはRe=11400であり，パッシブスカラー ϕの値は，上側(y≧0)でϕ=1，下側(y<0)でϕ=0とした．ϕに対する分子シュミット数はSc=ν/D=1.0である．ここで，Dはϕに対する分子拡散係数である．計算格子数はN_x×N_y×N_z=850×256×256であり，小さなスケールでの散逸を模擬するためのローパスフィルターはKennedy & Carpenter⁽⁹⁾によって提案されたexplicit tenth-order filterを使用した．差分法等の計算方法の詳細は文献(10)，(11)，(12)を参考にされたい．

3・2　計算結果

　図3はϕ=0.5の等値面と鉛直方向スカラーフラックスνϕの値をカラー表示で表したものである．また，グリッドスケールの速度こう配テンソルの第二不変量Qの値がQ>0となる領域を青色で示してある．図より，上流域では最も大きな格子棒の背後において大きなスカラーフラックスを示し，したがってスカラー混合層の鉛直方向への広がり速度も大きくなる．一方，下流域では中心近くの鉛直方向フラックスもまた大きくなっている．

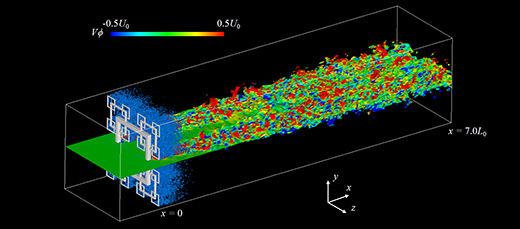
Fig.3 Three dimensional visualization of a scalar mixing layer. The isosurface of ϕ=0.5 is shown with a color which represents vertical scalar flux νϕ. The isosurface of second invariant of the resolved velocity gradient tensor (Q>0) is shown by blue.

　 図４(a),(b)には，フラクタル格子に近い位置x/L₀=1.8でのy軸方向の乱流輸送T_y=-∂<ν'ϕ'>/∂yおよびZ軸方向の乱流輸送T_z=-∂<w'ϕ'>/∂zの断面分布が示されている．ここで，L₀は最大格子棒の長さであり，プライム記号は変動成分を表す．図4(a)よりT_yは|z|L₀=0.5付近で，y=0の上と下でそれぞれ負と正の値を示していることがわかる．これにより最も大きな寸法の格子棒の背後において，乱流輸送項により平均スカラーは輸送され，スカラー混合層は|z|L₀=0.5付近で急速に発達することになる．一方，図4(b)より， |z|L₀=0.5付近の格子上部（y>0の領域）でT_zが正であり，その両サイドに負の領域が見られる．格子下部（y<0の領域）では，T_zの符号は逆転している．このようなT_zの分布より，格子上部では最も大きな格子棒の両サイド（外側および中央部）からスカラーが格子棒の背後に輸送され，格子下部では，逆に格子棒の背後から両サイドへスカラーが輸送されることを意味している．そして，このT_zの正負の値は中央部よりは外側の方が大きくなっている．したがって，スカラー場は外側つまり|z|L₀≧0.5の領域でy方向により早く広がると考えられる．図4(c), (d)には，フラクタル格子から離れた位置x/L₀=3.6でのT_yとT_zの断面分布がそれぞれ示されている．図4の(a)と(c) を比較するとわかるように，x/L₀=3.6では，格子中央部にも鉛直方向の輸送が存在する．これは，最も大きな格子棒の後流がx/L₀=3.6よりも上流側で融合しているからであると考えられる．x/L₀=3.6でのT_zの分布（図4(d)）はx/L₀=1.8での分布（図4(b)）と類似しているが，格子中央部上下にT_zの正負の値が大きい領域が集まり，その値は外側のT_zの正負の値と同程度であることがわかる，しかしながら，格子外縁部（|z|/L₀≧0.9）ではT_yは小さい値を示しているので，y方向の混合層の発展は中央部でより大きくなると考えられる．その結果，混合層はより下流ではスパン方向に一様な発展を示すようになると考えらえる．

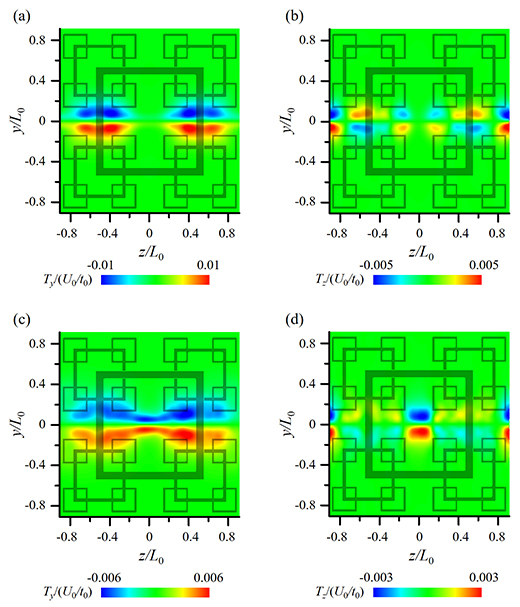
Fig.4 Cross-sectional profiles of turbulent diffusion term

(a) vertical direction	Tx =-∂<ν'ϕ'>/∂y at x/L0=1.8 ;
(b) horizontal direction	Tz =-∂<w'ϕ'>/∂z at x/L0=1.8 ;
(c) vertical direction	Tx =-∂<ν'ϕ'>/∂y at x/L0=3.6 ;
(d) horizontal direction	Tz =-∂<w'ϕ'>/∂z at x/L0=3.6 ;

 

4.　結　　　言

　 本稿では非平衡格子乱流場の特性とスカラー輸送機構に関する研究結果を紹介した．ひとつは4種類で合計11の格子を使用して，格子配置の非平衡特性発現への影響を調べた実験的研究であり，いまひとつは．ILESによる四角型フラクタル格子乱流中のパッシブスカラー混合層の発展に関する研究である．最初の実験的研究から，大きなスケールの格子とその周りに非一様に配置されたより小さな格子の組合せがより広い非平衡領域を生成する要因になっていることが示され，二つ目の数値シミュレーションによる研究では，四角型フラクタル格子乱流中に発展するパッシブスカラー混合層の発展は大きなスケールの格子背後に生じるスパン方向乱流拡散が重要な貢献をしていることが明らかにされた．今後の課題としては，上記のような“非平衡性”が発現する物理的メカニズムの解明と乱流混合・拡散現象などへのその工学的応用を探求することであると思われる．そのための理論的，実験的，数値的研究の活発な進展を期待したい．

 

謝　　　辞

　本研究は，主に，名古屋大学工学研究科機械理工学専攻，統計流体工学研究室で行われたものである．著者らは，実験の実施にあたり，当時大学院生であった祭貴哲平氏のご尽力に深い謝意を表します．また，数値計算の実施には東北大学流体科学研究所の早瀬敏幸教授との共同研究の一環として，流体科学研究所の大型計算機を使用させていただいた．早瀬敏幸教授にはここに記して謝意を表します．また，これらの研究の一部は文部科学省科学研究費，課題番号25002531，25289030，25289031，25630052の援助によって実施されました．ここに謝意を表します．　

 

文　　　献

(1)	Tennekes, H. and Lumley, J.L., “A first course in turbulence”，The MIT Press, 1972, p.68.
(2)	Rollin, B, Dubief, Y., and Dperomg, C.R., “Variations on Kolmogorov flow: turbulent energy dissipation and mean flow profiles”,  Journal of Fluid Mechanics, Vol.670 (2011), pp. 204-213.
(3)	Valente, P.C. and Vassilicos, J.C., “Universal dissipation scaling for nonequilibrium turbulence," Physical Review Letters, Vol.108 (2012),  214503.
(4)	Zhou, Y., Nagata, K., Sakai, Y., Suzuki, H., Ito,Y. and Hayase, T., “On the Evolution of the Invariants of the Velocity Gradient Tensor in the Single-Square-Grid-Generated Turbulence”,  Physics of Fluids, Vol.27 (2015), 075107.
(5)	Zhou, Y., Nagata, K., Sakai, Y., Ito, Y. and Hayase, T., “Spatial evolution of the helical behavior and 2/3 power-law in single-square-grid-generated turbulence”, Fluid Dynamics Research , Vol.48 (2016), 021404.
(6)	Sakai, Y., Zhou, Y., Nagata, K. and Ito, Y., “On the evolution of turbulent flow generated by single/fractal-square grid”, Bulletin of the 3rd EPSRC-ERCOFTAC Workshop on Turbulent Flows Generated/Designed in Multiscale/Fractal Ways: Fundamentals and Application, , London, UK, (2014),  p.6.
(7)	Nagata, K., Saiki, T., Sakai, Y., Ito, Y. and Iwano, K., “Effects of grid geometry on dissipation and non-equilibrium turbulence”, Physics of Fluids, submitted.
(8)	Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. and Hayase, T., “Implicit large eddy simulation of a scalar mixing layer in fractal grid turbulence”, Physica Scripta, Vol.91 (2016), 074007.
(9)	Kennedy, C.A. and Carpenter, M.H., “Several new numerical methods for compressible shear-layer simulations”, Applied Numerical Mathematics, Vol.14 (1994), pp.397-433.
(10)	Suzuki, H., Nagata, K., Sakai, Y. and Hayase, T., “Direct numerical simulation of turbulent mixing in regular and fractal grid turbulence”, Physica Scripta, Vol.T142 (2010), 014065.
(11)	Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. and Hayase, T., “Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers”, Physics of Fluids , Vol.27 (2015), 085109.
(12)	Watanabe, T., da Silva, C.B., Sakai, Y., Nagata, K. and Hayase, T., “Lagrangian properties of the entrainment across turbulent/ non-turbulent interface layers”, Physics of Fluids, Vol.28 (2016), 031701.