流れ　2016年11月号　目次

―　特集テーマ：2016年度年次大会　― 巻頭言 （藤井，横山，渡辺） 市場にデビューする相反転方式ターボ機械 金元敏明（佐賀大学） 非平衡格子乱流場の特性とスカラー輸送機構 酒井康彦，長田孝二, 伊藤靖仁, 渡邉智昭, 岩野耕始（名古屋大学） ワークショップ：複雑流体の新展開 山本剛宏（大阪電気通信大学），鳴海敬倫（新潟大学），蝶野成臣（高知工科大学） 複雑流体としての生物系粒子分散系 山本剛宏（大阪電気通信大学） 非アファイン性を考慮した高分子添加溶液におけるエネルギー伝達と抵抗低減 －働く高分子と働かない高分子－ 堀内潔（東京工業大学） EFDワークショップ：光学的流体計測手法 渕脇正樹（九州工業大学），飯尾昭一郎（信州大学），稲澤歩（首都大学東京），菊地聡（岐阜大学） 多レンズ多方向光学系の設計および瞬間CT法による非定常流体現象の三次元計測と３Dプリンティング 石野洋二郎（名古屋工業大学） 非定常熱流動場における壁近傍の速度-熱伝達の光学的同時計測について 山田俊輔（防衛大学校），中村元（防衛大学校） 　｜　リンク一覧にもどる　｜

 

複雑流体としての生物系粒子分散系

山本 剛宏 大阪電気通信大学

1. 緒言

　複雑流体は，流体内部に分子・原子スケールよりも大きなスケールの構造を有する流体である．そして，その内部構造が流動により変化することによって，複雑流体の特異な流動現象が引き起こされると考えられている．一方，微生物は自らが運動する能力を有し，他の個体や周囲環境との相互作用によりその行動を変化させる．このような微生物を，自己推進能をもつ一種の粒子（能動粒子）として捉えれば，生物系粒子分散流体は，流動や個体間相互作用，外場の影響によって構造が変化する能動粒子分散系であり，複雑流体のひとつと考えることができる．

　 我々は，このような発想から，微生物粒子分散流体に対して，複雑流体の流動解析手法を適用することで新たな数値解析モデルの構築が可能であると考えた．微生物の特徴的な挙動のひとつに，微生物が光度，重力，化学物質濃度，周囲個体の運動などの周囲環境に応じて運動を変える，走性と呼ばれる特性がある．微生物分散流体の数値解析モデルの開発の端緒として，走性を考慮したモデルの構築を進めた．ここでは，光度に応じて挙動を変化させる走光性を有する微細藻類の分散系の流れの数値解析を中心に，連続体力学的なアプローチと微生物個体を粒子として表現し，その運動を計算する粒子法的アプローチによる研究について紹介する．

 

2. 連続体力学的アプローチ

　 微生物分散系中の吸光による光度変化をLambert-Beer則によって計算し，微細藻類の走光性を走光性関数で表現する方法と組み合わせることで，微細藻類分散系の数密度分布の時間変化 ⁽¹⁾ を計算した．微細藻類の数密度の時間変化は，微細藻類の連続の式に基づいて導出される移流拡散方程式から求められる．

　 また，微生物分散流体の粘度が微生物の体積分率に依存することが実験によって確認されている ⁽²⁾．そこで，粘度の粒子体積分率依存性を，高濃度球形コロイド粒子分散系の粘度モデルとして提案されているKrieger-Doughertyモデルにより表現することで，微生物分布の非一様性の影響を取り入れた．そして，周囲から照明された円管内の微細藻類分散系の流れの解析 ⁽³⁾ を行った．そこでは，微細藻類の数密度分布や系の速度分布の照射光強度依存性やそれらのマクロ流動特性への影響が示された．

 

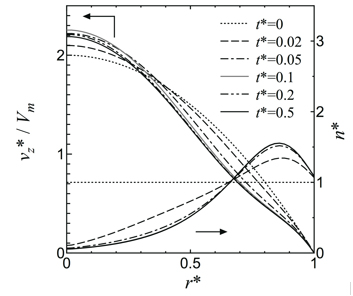
Fig. 1 Temporal changes in velocity profile ν_z^*/V_m and number density n* of flows of a microalgae suspension in a circular tube channel.

 

3. 粒子法的アプローチ

　 解析モデルに微生物の個性（個体差）を考慮したり，複数種の分散系を取り扱ったりするためには，各個体の特性を個別に表現し，それらの運動を計算することができる粒子法ベースのモデルが有用である．そこで我々は，Multi-Particle Collision Dynamics（MPCD）の適用を行った．

　 MPCDは流体を仮想粒子（溶媒粒子）の集合で表現し，粒子間の運動量交換を通じて流体の粘性を表現する手法である．また，MPCDは，近年，高分子流体やコロイド粒子分散系などの複雑流体の流動誘起構造解析にも適用されている ⁽⁴⁾．MPCDでは，粒子間衝突は，直接計算するのではなく，運動量交換を通じて統計的に処理されるために，多数の粒子を扱う計算において計算負荷を大幅に低減できる．

　 我々は，微細藻類を，自己推進能を有する能動粒子として表現し，連続体的手法で用いた走光性関数による走光性の表現を各粒子に適用することで，走光性をもつ能動粒子をモデル化した．そして，微細藻類間，微細藻類と溶媒（粒子）との相互作用を，MPCDを用いて表現した ^{(5, 6)}．

　 本モデルを平行平板間の圧力駆動流れ ⁽⁵⁾ やバイオ対流 ⁽⁶⁾ の解析に適用した．図2はバイオ対流の計算結果の例である．ここで示した計算では，微細藻類の排除体積効果や微生物の運動様式の効果は考慮されていないが，現在それらを考慮したモデルの構築に取り組んでいる．

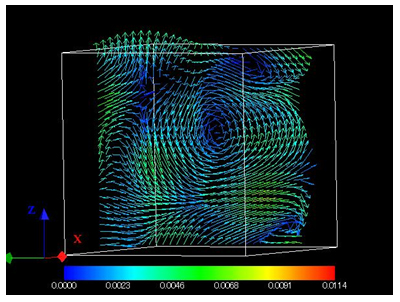
Fig. 2 Example of numerical results of MPCD simulation of bio-convection in a phototactic microalgae suspension: Snapshot of velocity field.

 

4. 結言

　微生物などの生物系粒子の分散系の流動現象は，複雑流体の新しい研究分野として，更なる展開が期待される分野である．今後，走性以外の特性を考慮したより生物らしいモデル粒子の開発を進めていく予定である．

 

謝辞

　 本研究は，JSPS科研費 JP25289032の助成を受けたものです．

 

文献

(1)	Ghorai, S. and Hill, N.A., “Penetrative Phototactic Bioconvection”, Physics in Fluids, Vol.17, No.7 (2005), 074101.
(2)	Mussler, M., Rafai, S., Peyla, P., and Wagner, C., “Effective Viscosity of Non-Gravitactic Chlamydomonas Reinhardtii Microswimmer Suspensions”, Europhysics Letters, Vol.101, No.5 (2013), 54004.
(3)	Yamamoto, T., “Numerical Simulation of the Flows of Phototactic Microalgae Suspensions in an Illuminated Circular Channel”, Nihon Reoroji Gakkaishi, Vol.43, Nos.3-4 (2015), pp.53-62.
(4)	Gompper, G., Ihle, T., Kroll, D.M., and Winkler, R.G., “Multi-Particle Collision Dynamics: A Particle-Based Mesoscale Simulation Approach to the Hydrodynamics of Complex Fluids”, Advances in Polymer Science, Vol.221 (2009), pp.1-87.
(5)	Yamamoto, T. and Nishiguchi, H., “Computational Model for Phototactic Microorganism Suspensions Using Multi Particle Collision Dynamics”, Abstract of 10th Annual European Rheology Conference (2015), p.50.
(6)	Yamamoto, T., Nakai, K., and Nishiguchi, H., “Development of Particle Method Based Model for Phototactic Microalgae Suspensions”, Abstract of the XVIIth International Congress on Rheology (2016), D4_M3_R2C.