流れ　2019年2月号　目次

―　特集テーマ：JSME年次大会特集　― 巻頭言 （本澤，黒沢） バイオミメティクスで流れを掴む技術の開発 窪田 佳寛（東洋大学），望月 修（東洋大学） プラズマアクチュエータ研究会 ～5年間の活動と今後の展望～ 瀬川 武彦（産業技術総合研究所），深潟 康二（慶應義塾大学），松野 隆（鳥取大学），野々村 拓（東北大学），大西 直文（東北大学） 効率的なトライ＆エラーによる流れ制御の研究 石川 仁（東京理科大学） コアンダノズルによる遷音速、超音速不足膨張噴流のベクトル制御 社河内 敏彦（三重大学） 主流と干渉する噴流による境界層能動制御 長谷川 裕晃（宇都宮大学） 多機能OCTによる毛細血管血流速マイクロ断層可視化法 佐伯 壮一（大阪市立大学），古川 大介（大阪市立大学），伊藤 高文（東光高岳），西野 佳昭（東光高岳） 多機能OCT によるスキンメカニクス診断への応用　～皮膚抹消血管構造の可視化～ 原 祐輔（資生堂グローバルイノベーションセンター），佐伯 壮一（大阪市立大学） 　｜　リンク一覧にもどる　｜

 

コアンダノズルによる遷音速，超音速不足膨張噴流のベクトル制御

社河内 敏彦 三重大学， 田ノ上 飛翔 三重大学， 辻本 公一 三重大学， 安藤 俊剛 三重大学

1.　緒言

　ノズルやスリットなどの小孔から空間中に速度をもった流体が噴出する噴流現象は，様々な分野で多用されているが，その流動特性はノズル形状や噴出速度, 及び周囲の状況などによって大きく異なる⁽¹⁾. また，ノズルマッハ数が約0.3を超えるような遷音速、及び超音速不足膨張噴流では噴流内に衝撃波が形成されるなど，流動特性は非圧縮性噴流とは大きく異なる．

　 ところで, 遷音速，及び超音速噴流は，それが噴出する際に生じる反力を用いて推力を得るジェットやロケット推進などで使用され，これらの性能を向上させるには, 推力の増加やベクトル制御などが挙げられる．従来，ジェットやロケットエンジンの推力ベクトルの制御には複雑な機構が用いられることが多く^{(2) ～ (4)}（図1, 2はそれぞれ，ジェット推進の3枚の可動ベーンによるベクトル制御，及びロケット推進のジンバル機構によるベクトル制御の例を示す．），これらの機構の簡易化はジェットやロケットエンジンにとって極めて重要である．

　 本研究では，コアンダ拡大ノズル（CC-nozzle）を取り付けたパイプノズルからの遷音速，超音速-不足膨張噴流のCC-nozzle の半径方向への移動による付着，偏向という比較的簡便な方法を使った噴流のベクトル制御について検討する．

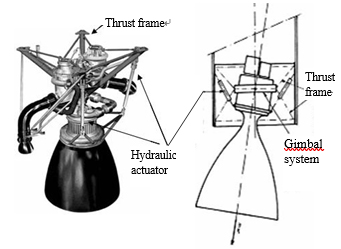Fig.1 Thrust-vectoring control system . (NASA photo EC90-177-4 with text added).	Fig.2 Rocket engine, Gimbal system http://www.zamandayolculuk.com/html-2/rocketdiagram.htm

2.　ノズルの詳細と制御方法

　図3(a) に，ノズル系を示す．ノズル系はノズル出口径3.7 mmのパイプノズル（Pi-ノズル）とコアンダノズル（CC-ノズル）からなる．CC-ノズルは，開き角度α = 7°, 10°, 14° で直線状に拡大し入口径はいずれも6.0 mmで，長さは12.0 mmである．座標系は，Pi-ノズルの出口中心を原点Oとし，中心軸をx軸，これに垂直な方向をr軸とした．

　 本研究ではCC-ノズルをPi-ノズルと同心円状に配置したノズル［Concentric nozzle, 図3(a)］，及びPi-ノズルの中心軸から1.15 mm 半径方向に移動させ，点Aでオフセット量を0 mmとして偏心円状に配置したノズル［Ec- centric nozzle, 図3(b)．この際，Pi-ノズルからの噴流はコアンダ効果により点A側に偏向，付着して流れる．］を用いて噴流のベクトル制御をおこなった．

(a) Concentric arrangement	(b) Eccentric arrangement
Fig.3 Arrangement of Pipe and Coanda nozzles

3.　フローパターン

　図4(a), (b) に，Pi-ノズルと同心軸上に設置されたα =10° のCC-ノズルからのP₀ = 0.380 MPa でのシュリーレン可視化画像を示す．また，図中の破線は，噴流の大略の外縁を示す．噴流は膨張，圧縮の衝撃波を伴いながらノズルの中心軸に沿って真っ直ぐに流下するStraight jet［St. jet, 図4(a)］，及びノズル内壁全周に渡って付着し拡大して流下するExpansion jet［Exp. jet, 図4(b)］の二つの安定な（二安定の）流動状態が存在する．

　 なお，二安定の状態にはP₀ の増減に従ってヒステリシス領域が存在した．

　 図4(c) に，Pi-ノズルの出口面とCC-ノズルの入口面が一箇所，点Aで内接するように設置されたα =10°のCC-ノズルからのP₀= 0.380 MPa でのシュリーレン可視化画像を示す．Pi-ノズルからの噴流は，コアンダ効果により内接した方向へ角度β = 6˚ で偏向しCC-ノズルの内面に付着して流れる（Deflection jet, Def. jet）．したがって，CC-ノズルを上記のように偏心，移動させることにより噴流のベクトルを制御することができる．

(a) Straight jet (concentric nozzle array)	(b) Expansion jet (concentric nozzle array)
(c) Deflection jet (eccentric nozzle array, β =6˚)
Fig.4 Visualized flow pattern (α=10°, P0=0.380 MPa)

4.　付着噴流の偏向角度，β

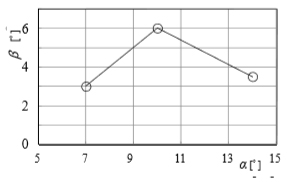
　図5に，P₀= 0.380 MPa でCC-ノズルを偏心させて設置した場合の噴流の偏向角度βを示す． βはαの増加とともに増加しα =10° で最大β =6° となった後，減少する．これは，α =14° ではCC-ノズルの開き角度が大きく噴流がCC-ノズルの壁面に十分付着できないことによると考えられる．

5.　速度分布

　図6に，α =10°, P₀= 0.380 MPa での中心線速度分布u_cを示す．u_cは，測定位置での総圧と静圧を直径1.0 mm の総圧，静圧管を使って求め流れの圧縮性を考慮して求めた．Pi-噴流は流れの膨張，圧縮に従って大きく変動しながら，u_c≒400 m/s で流下する．

　 CC-ノズルからのSt. jetは膨張，圧縮の衝撃波が小さく，速度の変動も小さい．これはCC-ノズルを設置したことによる流動損失の増加による．また，Def. jet は，CC-ノズルの片側のみに付着して流れるため（非付着側の噴流とノズル壁管の空間が大きく）ノズルの流動損失は小さく，x/d₀= 8.3 でのu_c はPi-噴流のそれとほぼ等しく，その後減衰する．Exp. jetでは，噴流はノズル壁全面に付着し半径方向に大きく拡大するためu_c はノズル出口近傍で極めて小さく，また，流下するにつれて噴流が中心に集合するため幾分大きくなる．

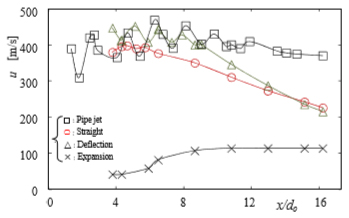Fig.5 Deflection angle, β	Fig.6 Centerline velocity distribution, uc (α =10˚, P0= 0.380 MPa)

　図6に，α =10°, P₀= 0.380 MPa での CC-噴流（Exp. jet, Def. jet）の断面速度分布uを示す．St. jetのuは（Pi-噴流と異なり）Goertler形の分布形をもち，流下するにつれて噴流幅が増加する．また，CC-ノズルによる流動損失のためPi-噴流より速度が小さかった．一方，Def. jetのuは流れの圧縮，膨張の結果，x/d₀ = 4.2, 5.4 で（Pi-噴流の場合と同様に）中心で極小値をとり，その後，流下するにしたがってGoertler形の分布形になる．また，St. jet の流速はDef. jetよりも幾分小さく，St. jet, Def. jetの半径方向への拡がりはともにPi-噴流より大きい．

　 図6(b)に，Exp. jetの結果を示す．Exp. jetはCC-ノズル壁面全面にわたって付着，拡大するため，流速が噴流の中心付近で小さく外縁周辺で大きい分布形をもち，最大流速は（St. jet）Def. jetに比べて極めて小さい．なお，他の噴流に比べ流動状態が全く異なり, ノズルの流動損失が極めて大きい. また, 噴流幅はSt. jetに比べて大きい．

6.　噴流の推力，F

　図7に，P₀= 0.380 MPa でのα =10° のCC-ノズルからの噴流の流れ方向の推力Fを示す．なお，推力Fは，図7に示した噴流のx/d₀ = 4.6（CC-ノズル出口直後）での断面速度分布を中心軸周りに積分して質量流量を求め，噴流の運動量変化として近似的に算出した⁽¹⁾．

(1)

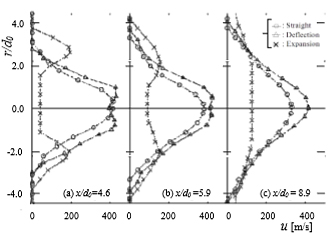
Fig.7 Velocity distribution at the cross section　(CC-nozzle, α =10°, P₀= 0.380 MPa)

　St. jetの推力（Fs= 3.1 [N]）はノズルの流動損失によりDef. jetより小さく，また，Exp. jetのFは他の噴流に比べて非常に小さい．例えば，Exp. jetのFはSt. Jetの約68%である．

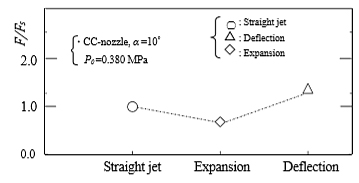
Fig.8 Total thrust, F, at the nozzle exit (at x/d₀ = 4.6)

7.　結　　　言

1. 流路が開き角度αで線形に拡大するコアンダノズル（CC-ノズル）からの噴流（供給圧力P₀ = 0.38 MPa）のフローパターンには，流れに衝撃波を伴いながらノズルの中心軸に沿って真っ直ぐ流下するStraight jet，流れがノズル壁全周にわたって付着し拡大するExpansion jet，及び流れに衝撃波を伴いながらノズルの片側のみに付着し偏向するDeflection jetの3つのフローパターンが存在する．
2. P₀= 0.380 MPa でCC-ノズルをパイプノズルの中心軸に対して偏心させて配置したノズル（パイプノズルとCC-ノズルのオフセット量：ゼロ）からの噴流の偏向角βは，α =10° で最大β = 6° となる．
3. P₀= 0.380 MPa でα =10°のCC-ノズルからのStraight jet, Deflection jet, Expansion jetの流れ方向の推力はそれぞれ，F = 3.1, 2.2, 4.3 [N]である．

　以上，コアンダ（拡大）ノズル（CC-nozzle）を主ノズル（Pi-nozzle）に対して偏心させることにより，従来よりも可動部の少ない簡便な方法で遷音速，超音速不足膨張噴流のベクトル制御が可能であることを示した．

　現在，機械的な可動部を持たず，流体の流れのみで主流れを制御するフルイディクス的なベクトル制御（Fluidic Thrust Vectoring）について検討している．

参考文献

(1)	Zaman, K.B.M.Q., Spreading characteristics of compressible jets from nozzles of various geometries, J. of Fluid Mech., Vol.383 (1999), pp.197-228.
(2)	Trancossi, M. and Dumas, A., Coanda synthetic jet deflection apparatus and control, SAE International, 2011-01-2590 (2011).
(3)	Allen, D.S., Axisymmetric Coanda-assisited vectoring, Master’s thesis of Utah State Univ., (2008).
(4)	Mason, M.S. and Crowther, W.J., Fluidic thrust vectoring of low observable aircraft, Proc. of CEAS Aerospace Aero- dynamic Research Conf., (2002, Cambridge, UK).